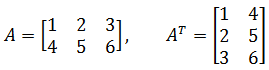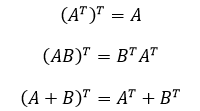刷穿力扣（31~60）
liyusendesu
|
ALGORITHM,Q&A
|
|
1,529
|
0

3237 字
|
47 分钟
本文最后更新于 387 天前，其中的信息可能已经有所发展或是发生改变。

31. 下一个排列

  • 排列
  • 原理就是 C++ 中的 next_permutation 函数，生成指定序列的下一个全排列
  • 从给定序列的最右端开始，找到第一个满足 nums[i] < nums[i + 1] 的元素 nums[i]
  • 若找不到这样的元素 nums[i]：说明当前序列是最后一个排列，函数将序列重排为第一个排列，并返回 false
  • 若找到了元素 nums[i]：继续从最右端开始，找到第一个满足 nums[i] < nums[j] 的元素 nums[j]。
  • 交换 nums[i] 和 nums[j]，然后从 i + 1 开始将序列反转，使得它们按照升序排列。
class Solution {
    public void nextPermutation(int[] nums) {
        int n = nums.length;
        int i = n - 2;
        while (i >= 0 && nums[i] >= nums[i + 1]) i --;
        if (i >= 0) {
            int j = n - 1;
            while (nums[j] <= nums[i]) j --;
            swap(nums, i, j);
        }
        reverse(nums, i + 1, n - 1);
    }

    private void swap(int[] nums, int i, int j) {
        int t = nums[i];
        nums[i] = nums[j];
        nums[j] = t;
    }

    private void reverse(int[] nums, int l, int r) {
        while (l < r) {
            this.swap(nums, l, r);
            l ++; r --;
        }
    }

}

32. 最长有效括号

  • 栈
  • 用 Stack<Integer> 存储所有 ( 的下标
  • 当遇到右括号时，检查栈是否为空：
    • 若栈为空，则说明当前右括号没有匹配的左括号，将当前右括号的位置作为新的起始位置。
    • 若不为空，则弹出栈顶元素，并更新当前有效括号的长度（当前右括号的位置减去栈顶元素的值）
  • 遍历完字符串后，得到最长有效括号的长度
class Solution {
    public int longestValidParentheses(String s) {
        Stack<Integer> stack = new Stack<>();
        int ans = 0;
        int start = -1; // 有效括号序列的起始位置

        for (int i = 0; i < s.length(); i++) {
            // 将左括号的位置压入栈中
            if (s.charAt(i) == '(') stack.push(i); 
            else {
                if (stack.isEmpty()) {
                    start = i; // 当前右括号无法匹配，更新起始位置
                } 
                else {
                    stack.pop();
                    // 栈为空，表示当前右括号匹配到有效括号序列的末尾
                    if (stack.isEmpty()) ans = Math.max(ans, i - start);
                    else ans = Math.max(ans, i - stack.peek());  // 栈不为空，计算当前有效括号序列的长度
                }
            }
        }

        return ans;
    }
}

优化：

  • 模拟
  • 设当前的括号出现的次数 res，第一次扫代表 (，起始位置 l = 0，第二次扫代表 )，起始位置 r = n - 1
  • 先从左往右扫一遍，若为 (，res ++；
  • 当遇到 ) 时:
    • 若 res == 0，则更新最长有效括号的长度 ans，并更新起始位置 l
    • 否则：说明匹配，res --，若此时 res == 0，则匹配了全部左括号，更新 ans
  • 第一遍扫完后，判断是否还有未匹配的左括号。如果没有或者最长有效括号的长度 ans 已经大于等于剩余未匹配左括号的长度（n - l），则直接返回 ans。
  • 如果还有未匹配的左括号，说明可能出现以右括号结尾的有效括号序列。再从右往左扫第二遍，步骤是一样的。
  • 最终返回最长有效括号的长度 ans。
class Solution {
    public int longestValidParentheses(String s) {
        int res = 0;
        int n = s.length();
        int ans = 0, l = 0;
        // 从左扫第一遍
        for (int i = 0; i < n; i ++) {
            if (s.charAt(i) == '(') {
                res ++; continue;
            }
            // 遇到右括号，且当前没有匹配的左括号
            if (res == 0) {
                ans = Math.max(ans, i - l);  // 更新最长有效括号的长度
                l = i + 1;  // 更新起始位置
            } 
            else {
                res --;  // 遇到右括号，且有匹配的左括号，res --
                if (res == 0) ans = Math.max(ans, i - l + 1);
            }
        }
         // 如果遍历完字符串后，仍有未匹配的左括号
        if (res == 0 || ans >= n - l) return ans;

        int r = n - 1; res = 0;
        // 从右扫第二遍
        for (int i = n - 1; i > l; i --) {
            if (s.charAt(i) == ')') {
                res ++; continue;
            }
            if (res == 0) {
                ans = Math.max(ans, r - i);
                r = i - 1;
            } 
            else 
                res --;
                if (res == 0) ans = Math.max(ans, r - i + 1);
            }
        }

        return ans;
    }
}

33. 搜索旋转排序数组

  • 二分
  • 显然，在旋转点的左侧满足 nums[i] >= nums[0]，而右侧 nums[i] < nums[0]
  • 根据上述的单调性我们第一次二分找到旋转点的位置
  • 然后判断 target 在旋转点的左半部分还是右半部分
  • 显然，当 target >= nums[0] 时在左半部分
  • 然后继续二分，更新 l, r 为新的目标区间继续查找
class Solution {
    public int search(int[] nums, int target) {
        int n = nums.length;
        if (n == 1) return nums[0] == target ? 0 : -1;
        int l = 0, r = n - 1;
        // 寻找旋转点，查找第一个不满足 >= nums[0] 的元素下标
        while (l <= r) {
            int mid = (l + r) >> 1;
            if (nums[mid] == target) return mid;
            if (nums[mid] >= nums[0]) l = mid + 1;
            else r = mid - 1; 
        }
        if (l < n && nums[l] == target) return l;
        // 判断 target 在左半区间还是右半区间
        if (target >= nums[0]) {
            r = l - 1; l = 0;  // 更新边界为左半区间
        }
        else {
            l ++; r = n - 1;   // 更新边界为右半区间
        }
        // 在剩下半个区间查找 == target 的元素下标
        while (l <= r) {
            int mid = (l + r) >> 1;
            if (nums[mid] == target) return mid;
            if (nums[mid] < target) l = mid + 1;
            else r = mid - 1;
        }
        return l < n && nums[l] == target ? l : -1;
    }
}

34. 在排序数组中查找元素的第一个和最后一个位置

  • 二分
  • 数组已从小到大排序，满足单调性
  • 第一遍二分寻找第一个小于 target 的数，期间更新 nums[mid] == target 的下标，即为第一个位置
  • 第二遍二分寻找第一个大于 target 的数，期间更新 nums[mid] == target 的下标，即为第二个位置
class Solution {
    public int[] searchRange(int[] nums, int target) {
        int n = nums.length;
        int l = 0, r = n - 1;
        int res = -1;
        while (l <= r) {
            int mid = (l + r) >> 1;
            if (nums[mid] == target) res = mid;
            if (nums[mid] < target) l = mid + 1;
            else r = mid - 1;
        }
        if (res == -1) return new int[]{-1, -1};
        l = res; r = n - 1;  // l 从 res 开始或 0 开始都行
        int cnt = -1;
        while (l <= r) {
            int mid = (l + r) >> 1;
            if (nums[mid] == target) cnt = mid;
            if (nums[mid] > target) r = mid - 1;
            else l = mid + 1;
        }
        return new int[]{res, cnt};
    }
}

35. 搜索插入位置

  • 二分
  • 没啥好说的板子题
class Solution {
    public int searchInsert(int[] nums, int target) {
        int l = 0, r = nums.length - 1;
        while (l <= r) {
            int mid = (l + r) >> 1;
            if (nums[mid] == target) return mid;
            if (nums[mid] < target) l = mid + 1;
            else r = mid - 1;
        }
        return l;
    }
}

36. 有效的数独

  • 模拟
  • 只需要验证已有的数是否符号规则就行，因此我们可以用区区十几个循环嵌套来解决
  • 首先将数独按照 $3 \times 3$ 分为 $9$ 组，然后用 boolean[][] 维护每组格子的状态
  • 具体滴，对于格子 board[i][j]，所在的组编号 u 映射为 u = i / 3 * 3 + j / 3
  • 则 boolean[][] vis[u][num] 表示第 u 组数字 num 是否已经存在
  • 那么除此之外，还需要判断行和列的格子的状态即可
class Solution {
    public boolean isValidSudoku(char[][] board) {
        boolean[][] vis = new boolean[10][10];  // 记录小方块的填数状态
        boolean[][] row = new boolean[10][10];  // 记录每一行的填数状态
        boolean[][] col = new boolean[10][10];  // 记录每一列的填数状态

        for (int i = 0; i < 9; i ++) {
            for (int j = 0; j < 9; j ++) {
                char t = board[i][j];
                if (t == '.') continue;  // '.' 无所谓，直接跳过
                int num = t - '0';
                // 组编号映射
                int u = i / 3 * 3 + j / 3;
                // 只要有一个已经存放过都不成立
                if (vis[u][num] || row[i][num] || col[j][num]) return false;
                vis[u][num] = row[i][num] = col[j][num] = true;
            }
        }
        return true;
    }
}

37. 解数独

  • DFS
  • 对于 board[i][j] 从 $1 \sim 9$ 暴力搜索每一个可能的值
  • 难点仍是在于判断是否合法，思路同上一题
class Solution {
    public void solveSudoku(char[][] board) {
        boolean[][] vis = new boolean[10][10];  // 记录每个数字在每一行的填数状态
        boolean[][] row = new boolean[10][10];  // 记录每个数字在每一列的填数状态
        boolean[][] col = new boolean[10][10];  // 记录每个数字在每个小方块的填数状态
        init(board, vis, row, col);  // 初始化状态数组
        dfs(board, 0, 0, vis, row, col);
    }

    private boolean dfs(char[][] board, int i, int j, boolean[][] vis,
                    boolean[][] row, boolean[][] col) {
        if (i == 9) return true;  // 数独已经填满，返回 true
        if (j == 9) return dfs(board, i + 1, 0, vis, row, col);  // 当前行已经填完，转到下一行
        if (board[i][j] != '.') return dfs(board, i, j + 1, vis, row, col);  // 当前位置已经有数字，转到下一个位置
        // 从 1 开始枚举可能的值
        for (int num = 1; num <= 9; num ++) {
            int idx = i / 3 * 3 + j / 3;  // 小方块的索引
            if (!vis[idx][num] && !row[i][num] && !col[j][num]) {
                vis[idx][num] = row[i][num] = col[j][num] = true;
                board[i][j] = (char)(num + '0');  // 填入值
                if (dfs(board, i, j + 1, vis, row, col)) return true;  // 递归填下一个位置
                // 恢复现场
                vis[idx][num] = row[i][num] = col[j][num] = false;     
                board[i][j] = '.';
            }
        }
        return false;  // 无法填入任何数字，返回false
    }

    private void init(char[][] board, boolean[][] vis,
                    boolean[][] row, boolean[][] col) {
        for (int i = 0; i < 9; i ++) {
            for (int j = 0; j < 9; j ++) {
                if (board[i][j] != '.') {
                    int num = board[i][j] - '0';
                    int idx = i / 3 * 3 + j / 3;
                    vis[idx][num] = row[i][num] = col[j][num] = true;
                }
            }
        }
    }
}

38. 外观数列

  • DFS
  • 递归的每一层，对上一层生成的 s 进行遍历
  • 用 char flag 记录当前的字符，cnt 记录当前字符的数量
  • 用 StringBuilder sb 来接收对 s 的描述并且继续搜索
class Solution {
    public String countAndSay(int n) {
        return dfs(n, 1, "1");
    }

    private String dfs(int n, int u, String s) {
        if (u == n) return s;
        StringBuilder sb = new StringBuilder();
        int cnt = 0;
        char flag = s.charAt(0);
        for (int i = 0; i < s.length(); i ++) {
            if (s.charAt(i) == flag) cnt ++;
            else {
                // 当前字符和 flag 不同，说明发生改变
                sb.append(cnt); sb.append(flag);  // 将 flag 字符及其数量 cnt 描述加入 sb
                flag = s.charAt(i); cnt = 1;      // 更新 flag 和 cnt
            }
        }
        // 添加最后一个字符的计数
        sb.append(cnt); sb.append(flag);
        return dfs(n, u + 1, sb.toString());
    }
}

39. 组合总和

  • DFS
  • 首先对 candidates 从小到大排序
  • 递归的每一层视作对 candidates[i] 的选择
  • 由于数组是从小到大单调的，当 cnt + candidates[i] > target 即可不用在向后遍历
class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        Arrays.sort(candidates);
        List<List<Integer>> ans = new ArrayList<>();  // 存储答案
        List<Integer> res = new ArrayList<>();        // 存储递归每一层的结果
        dfs(candidates, target, 0, 0, res, ans);
        return ans;
    }

    private void dfs(int[] candidates, int target, int u, int cnt, 
        List<Integer> res, List<List<Integer>> ans) {
        if (cnt == target) {  // 找到答案
            ans.add(new ArrayList<>(res));  // 将当前结果加入答案
            return ;
        }
        // 从 u 开始选择（因为可以重复）
        for (int i = u; i < candidates.length; i ++) {
            if (cnt + candidates[i] <= target) {  // 满足条件才能递归到下一层
                res.add(candidates[i]);
                dfs(candidates, target, i, cnt + candidates[i], res, ans);
                res.remove(res.size() - 1);  // 恢复现场
            } 
            else break;
        }
    }
}

40. 组合总和 II

  • DFS
  • 和上一题思路一样，不同的是不能包含重复选择
  • 有两种方式：
    • 添加 HashSet<Integer> vis 标记使用过的数
    • 在选择时加一层判断 candidates[i] == candidates[i - 1] 时跳过
class Solution {
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        Arrays.sort(candidates);
        List<List<Integer>> ans = new ArrayList<>();  // 存储答案
        List<Integer> res = new ArrayList<>();        // 存储递归每一层的结果
        dfs(candidates, target, 0, 0, res, ans);
        return ans;
    }

    private void dfs(int[] candidates, int target, int u, int cnt, 
        List<Integer> res, List<List<Integer>> ans) {
        if (cnt == target) {  // 找到答案
            ans.add(new ArrayList<>(res));  // 将当前结果加入答案
            return ;
        }
        for (int i = u; i < candidates.length; i ++) {
            if (i > u && candidates[i] == candidates[i - 1]) continue;
            if (cnt + candidates[i] <= target) {  // 满足条件才能递归到下一层
                res.add(candidates[i]);
                dfs(candidates, target, i + 1, cnt + candidates[i], res, ans);
                res.remove(res.size() - 1);  // 恢复现场
            } 
            else break;
        }
    }
}

<<<<<<< HEAD

41. 缺失的第一个正数

  • 模拟
  • 将数组本身视作哈希表
  • 预处理 nums[i] <= 0 || nums[i] > n 的值为 n + 1，表示不存在
  • 将出现的正数对应的位置标记为负数，通过改变正数对应位置上的符号来标记该位置所对应的数值已经出现过
  • 最后，遍历找到第一个为正数的位置，即为缺失的最小正整数。
class Solution {
    public int firstMissingPositive(int[] nums) {
        int n = nums.length;
        // 第一次遍历，将所有负数和大于 n 的数置为 n + 1
        for (int i = 0; i < n; i ++) {
            if (nums[i] <= 0 || nums[i] > n) nums[i] = n + 1;
        }

        // 第二次遍历，将出现的正数对应的位置标记为负数
        for (int i = 0; i < n; i ++) {
            int num = Math.abs(nums[i]);
            if (num <= n) nums[num - 1] = -Math.abs(nums[num - 1]);
        }

        // 第三次遍历，找到第一个正数的位置，即为缺失的最小正整数
        for (int i = 0; i < n; i ++) {
            if (nums[i] > 0) return i + 1;
        }

        // 如果数组中的所有数都出现了，返回 n + 1
        return n + 1;
    }
}

42. 接雨水

  • 单调栈
  • 维护 height[i] 之前出现过的最高的挡板
  • 对于 height[i] < height[st.peek()] 说明后面可能存在更高的挡板
  • 否则应当结算之前所接到的雨水
class Solution {
    public int trap(int[] height) {
        Stack<Integer> st = new Stack<>();
        int ans = 0;
        for (int i = 0; i < height.length; i++) {
            if (!st.isEmpty() && height[i] > height[st.peek()]) {
                int t = st.pop();
                if (st.isEmpty()) break;
                int l = i - st.peek() - 1;
                int r = Math.min(height[i], height[st.peek()]) - height[t];
                ans += l * r;
            }
            st.push(i);
        }
        return ans;
    }
}

43. 字符串相乘

  • 模拟
  • 字符串模拟乘法过程即可
class Solution {
    public String multiply(String num1, String num2) {
        if (num1.equals("0") || num2.equals("0")) return "0";
        int m = num1.length();
        int n = num2.length();
        int[] res = new int[m + n];  // 维护每一层乘法的结果
        for (int i = m - 1; i >= 0; i--) {
            int x = num1.charAt(i) - '0';
            for (int j = n - 1; j >= 0; j--) {
                int y = num2.charAt(j) - '0';
                res[i + j + 1] += x * y;  // 记录结果
            }
        }
        int base = 0;
        for (int i = m + n - 1; i >= 0; i--) {
            int sum = res[i] + base;
            res[i] = sum % 10;
            base = sum / 10;
        }
        StringBuilder sb = new StringBuilder();
        for (int num : res) sb.append(num);
        while (sb.length() > 0 && sb.charAt(0) == '0') sb.deleteCharAt(0);
        return sb.toString();
    }
}

44. 通配符匹配

  • dp
  • 第二题青春版
  • 状态表示：
    • 设 dp[i][j] 表示字符串 s 的前 i 个字符和字符串 p 的前 j 个字符是否匹配。
    • 初始化 dp[0][0] 为 true，表示空字符串和空模式是匹配的。
    • 初始化所有 * 之前的状态为 true，因为 * 可以匹配空字符串。

  • 状态计算：

    • 如果 p 的当前字符是 *，则可以选择匹配空字符串 dp[i][j-1] 或者匹配多个字符 dp[i-1][j]，只要有一个为 true，则 dp[i][j] 也为 true。
    • 如果 p 的当前字符是 ?，或者 p 的当前字符和 s 的当前字符相等，则将 dp[i][j] = dp[i-1][j-1]，表示当前位置的匹配状态与前一个位置的匹配状态相同。
    • 否则，dp[i][j] 为 false，表示当前位置的字符不匹配。
class Solution {
    public boolean isMatch(String s, String p) {
        int n = s.length(), m = p.length();
        boolean[][] dp = new boolean[n + 1][m + 1];
        dp[0][0] = true;
        // 初始化所有 * 之前的状态都为 true
        for (int i = 1; i <= m; i ++) {
            if (p.charAt(i - 1) == '*') dp[0][i] = true;
            else break;
        }
        for (int i = 1; i <= n; i ++) {
            for (int j = 1; j <= m; j ++) {
                if (p.charAt(j - 1) == '*') dp[i][j] = dp[i - 1][j] || dp[i][j - 1];
                else if (p.charAt(j - 1) == '?' || s.charAt(i - 1) == p.charAt(j - 1)) dp[i][j] = dp[i - 1][j - 1];
            }
        }
        return dp[n][m];
    }
}

45. 跳跃游戏 II

  • 贪心
  • 对于当前所处的位置 i，当 i + nums[i] >= n - 1 时可以直接返回结果
  • 否则，从 j = i 遍历到 j = i + nums[i]，设下一步的位置为 res，以 res 能到达的最远位置为 idx
  • 显然， j + nums[j] 即为下一步可以到达的最远位置 idx
  • 则只需找到 j + nums[j] 的最大值，并用 res 维护下一步的坐标 j 即可
class Solution {
    public int jump(int[] nums) {
        int ans = 0, n = nums.length;
        if(n <= 1) return 0;  // 当长度只有 1 时无需操作
        for(int i = 0; i < n; i ++){
            int res = 0, idx = 0;
            if(i + nums[i] >= n - 1) return ans + 1;  // 下一步的最远距离正好到达终点
            for(int j = i + 1; j <= i + nums[i]; j ++){  // 遍历找到能到达最远距离的方案
                if(j + nums[j] >= idx){
                    idx = j + nums[j];
                    res = j;
                }
            }
            i = res - 1; ans ++;  // 更新 i 和 ans
        }
        return ans;
    }
}

46. 全排列

  • 排列
  • [31. 下一个排列](#31. 下一个排列) 题无修版（
  • 先将给出的数组按照从小到大排序，以最小字典序寻找下一个全排列
  • 找不到全排列直接返回
class Solution {
    public List<List<Integer>> permute(int[] nums) {
        Arrays.sort(nums);
        List<List<Integer>> ans = new ArrayList<>();
        ans.add(this.asList(nums));
        while (nextPermutation(nums)) ans.add(this.asList(nums));
        return ans;
    }

    public boolean nextPermutation(int[] nums) {
        int n = nums.length, i = n - 2;
        while (i >= 0 && nums[i] >= nums[i + 1]) i --;
        if (i >= 0) {
            int j = n - 1;
            while (nums[j] <= nums[i]) j --;
            swap(nums, i, j);
            this.reverse(nums, i + 1, n - 1);
            return true;
        }
        else return false;  // 找不到直接返回
    }

    private void swap(int[] nums, int i, int j) {
        int t = nums[i];
        nums[i] = nums[j]; nums[j] = t;
    }

    private void reverse(int[] nums, int l, int r) {
        while (l < r) {
            this.swap(nums, l, r);
            l ++; r --;
        }
    }

    private List<Integer> asList(int[] nums) {
        List<Integer> res = new ArrayList<>();
        for (int num : nums) res.add(num);
        return res;
    } 
}

47. 全排列 II

  • 排列
  • 和上一题一毛一样
class Solution {
    public List<List<Integer>> permuteUnique(int[] nums) {
        Arrays.sort(nums);
        List<List<Integer>> ans = new ArrayList<>();
        ans.add(this.asList(nums));
        while (nextPermutation(nums)) ans.add(this.asList(nums));
        return ans;
    }

    public boolean nextPermutation(int[] nums) {
        int n = nums.length, i = n - 2;
        while (i >= 0 && nums[i] >= nums[i + 1]) i --;
        if (i >= 0) {
            int j = n - 1;
            while (nums[j] <= nums[i]) j --;
            swap(nums, i, j);
            this.reverse(nums, i + 1, n - 1);
            return true;
        }
        else return false;  // 找不到直接返回
    }

    private void swap(int[] nums, int i, int j) {
        int t = nums[i];
        nums[i] = nums[j]; nums[j] = t;
    }

    private void reverse(int[] nums, int l, int r) {
        while (l < r) {
            this.swap(nums, l, r);
            l ++; r --;
        }
    }

    private List<Integer> asList(int[] nums) {
        List<Integer> res = new ArrayList<>();
        for (int num : nums) res.add(num);
        return res;
    } 
}

48. 旋转图像

  • 矩阵转置
  • 用线性代数的知识，先将矩阵转置，再翻转即可
  • 将矩阵 $A$ 的行换成同序数的列得到的新的矩阵，叫做 $A$ 的转置矩阵，记作： $A^T$。
  • 转置运算公式：
    )
class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        // 先进行矩阵的转置操作
        for (int i = 0; i < n; i ++) {
            for (int j = i; j < n; j ++) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
        }
        // 再进行每行的翻转操作
        for (int i = 0; i < n; i ++) {
            for (int j = 0; j < n / 2; j ++) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[i][n - 1 - j];
                matrix[i][n - 1 - j] = temp;
            }
        }
    }
}

49. 字母异位词分组

  • 哈希表
  • 对于 strs[i] 将其按照字典序排序并映射下标，保存到 HashMap 中
  • 每次找到相同的排序后的映射，将其加入到答案 List[i] 后面即可
class Solution {
    public List<List<String>> groupAnagrams(String[] strs) {
        List<List<String>> ans = new ArrayList<>();
        HashMap<String, Integer> vis = new HashMap<>();
        int idx = 0;
        for (String s : strs) {
            char[] t = s.toCharArray();
            Arrays.sort(t);  // 得到字典序
            String st = new String(t);
            // 根据字典序 st 查找是否存在该映射 
            if (vis.containsKey(st)) ans.get(vis.get(st)).add(s);  // 存在则对应索引的 list add(s)
            else {
                // 不存在 创建新的 list
                List<String> newList = new ArrayList<>();
                newList.add(s); ans.add(newList);
                vis.put(st, idx ++);  // 记录映射
            }
        }
        return ans;
    }
}

50. Pow(x, n)

class Solution {
    public double myPow(double x, int n) {
        if (x == 0.0d) return 0.0d;
        long k = n;
        double res = 1.0d;
        if (k < 0) {
            x = 1 / x;
            k = -k;
        }
        while (k > 0) {
            if ((k & 1) == 1) res *= x;
            x *= x;
            k >>= 1;
        }
        return res;
    }
}

51. N 皇后

  • DFS
  • 递归的每一层，只能放一次棋子
  • 对于每个棋子，必须保证其斜率 $1$ 和 $-1$ 的直线上和这一列上没有相同的棋子
  • 即对于棋子 [i][j] 在斜率为 $1$ 和 $-1$ 时判断其截距是否已经存在即可，且要求 j 列不存在相同的棋子 
class Solution {
    public List<List<String>> solveNQueens(int n) {
        boolean[] col = new boolean[n];
        boolean[] l = new boolean[n * 2 + 1];
        boolean[] r = new boolean[n * 2 + 1];
        List<String> res = new ArrayList<>();
        List<List<String>> ans = new ArrayList<>();
        dfs(0, n, col, l, r, res, ans);
        return ans;
    }

    void dfs(int u, int n, boolean[] col, boolean[] l, boolean[] r, 
            List<String> res, List<List<String>> ans) {
        if (u == n) {
            ans.add(new ArrayList<>(res));
            return ;
        }
        char[] s = new char[n];
        for (int i = 0; i < n; i ++) s[i] = '.';
        for (int i = 0; i < n; i ++) {
            // 判断是否冲突
            if (!col[i] && !l[u - i + n] && !r[u + i]) {
                col[i] = l[u - i + n] = r[u + i] = true;  // u - i + n 防止 u - i < 0 越界
                s[i] = 'Q';
                res.add(new String(s));
                dfs (u + 1, n, col, l, r, res, ans);
                // 恢复现场
                res.remove(res.size() - 1);
                s[i] = '.';
                col[i] = l[u - i + n] = r[u + i] = false;
            }
        }
    }
}

52. N 皇后 II

  • DFS
  • 上一题青春版
  • 只需要维护方案数量即可，不需要记录答案
class Solution {
    private int ans;

    public int totalNQueens(int n) {
        boolean[] col = new boolean[n];
        boolean[] l = new boolean[n * 2 + 1];
        boolean[] r = new boolean[n * 2 + 1];
        return dfs (0, n, col, l, r);
    }

    int dfs(int u, int n, boolean[] col, boolean[] l, boolean[] r) {
        if (u == n) return 1;
        int res = 0;
        for (int i = 0; i < n; i ++) {
            // 判断是否冲突
            if (!col[i] && !l[u - i + n] && !r[u + i]) {
                col[i] = l[u - i + n] = r[u + i] = true;  // u - i + n 防止 u - i < 0 越界
                res += dfs (u + 1, n, col, l, r);
                col[i] = l[u - i + n] = r[u + i] = false;  // 恢复现场
            }
        }
        return res;
    }
}

53. 最大子数组和

  • dp
  • 状态表示：
    • dp[i] 表示以 nums[i] 结尾的数组中，最大的连续子数组的值
  • 状态计算：
    • 若 dp[i] <= 0 说明前面的数组没有继续扩展的需要，以 dp[i] 结尾的最大值为 Math.max(dp[i - 1], nums[i])
    • 否则，最大值为 dp[i - 1] + nums[i]
class Solution {
    public int maxSubArray(int[] nums) {
        int n = nums.length;
        int[] dp = new int[n];
        dp[0] = nums[0];    // 初始化
        int ans = nums[0];  // ans 维护 dp 的最大值结果
        for (int i = 1; i < n; i ++) {
            if (dp[i - 1] > 0) dp[i] = dp[i - 1] + nums[i];
            else dp[i] = Math.max(dp[i - 1], nums[i]);
            ans = Math.max(ans, dp[i]);
        }
        return ans;
    }
}

54. 螺旋矩阵

  • 模拟
  • 本质就是蛇形矩阵
  • 按照旋转的顺时针方向构建偏移量数组
  • 设 l, r 为当前遍历位置的坐标：
    • 若 l < 0 || r < 0 || l >= n || r >= m 说明越界，此时要按照顺时针方向转向
    • 若 vis[l][r] 已经被标记过，说明之前已经走过这个位置，显然也是越界行为，也要转向
  • 遍历的步数为 n * m
class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        int n = matrix.length, m = matrix[0].length;
        boolean[][] vis = new boolean[n][m];    // 作为标记数组判断是否走过该点
        List<Integer> ans = new ArrayList<>();  // 记录答案
        int x = 0, y = 0, d = 0;
        int[] dx = {0, 1, 0, -1}, dy = {1, 0, -1, 0};  // 构建偏移量数组，d = 0 表示向 -> 走的偏移量
        for (int i = 0; i < n * m; i ++) {
            ans.add(matrix[x][y]); vis[x][y] = true;   // 将走过的点标记 
            int l = x + dx[d], r = y + dy[d];          // l 和 r 为下一步要走的点，此时进行判断
            if (l < 0 || r < 0 || r >= m || l >= n || vis[l][r]) {
                d = (d + 1) % 4;               // 得到下一个偏移量
                l = x + dx[d]; r = y + dy[d];  // 重新更新 l, r
            }
            x = l; y = r;  // 更新 x, y
        }
        return ans;
    }
}

55. 跳跃游戏

  • 模拟
  • 45 的青春版
  • 用 idx 记录可以到达的最大位置的下标
  • 每次循环：
    • 若 i > idx 说明当前位置 i 无法到达，直接 false
    • 更新 idx = Math.max(idx, i + nums[i])
    • 若 idx >= nums.length - 1 说明已经可以到达尾部，直接 true
class Solution {
    public boolean canJump(int[] nums) {
        int idx = 0;
        for (int i = 0; i < nums.length; i++) {
            if (i > idx) return false; // 当前位置无法到达
            idx = Math.max(idx, i + nums[i]);
            if (idx >= nums.length - 1) {
                return true; // 已经可以到达最后一个位置
            }
        }
        return false;
    }
}

56. 合并区间

  • 区间合并
  • 板子题
  • 对区间左端点排序，判断前一个区间的右端点和当前区间的左端点关系
  • 若前一个区间的右端点小于等于当前区间左端点，说明可以合并，更新右端点
  • 否则当前区间为新的区间
class Solution {
    public int[][] merge(int[][] intervals) {
        int n = intervals.length;
        Arrays.sort(intervals, (o1, o2) -> o1[0] - o2[0]);  // 按照左端点从小到大排序
        List<int[]> ans = new ArrayList<>();
        int l = intervals[0][0], r = intervals[0][1];
        for (int i = 1; i < n; i ++) {
            // 合并操作
            if (intervals[i][0] <= r) r = Math.max(intervals[i][1], r);
            else {
                ans.add(new int[]{l, r});
                l = intervals[i][0]; r = intervals[i][1];
            }
        }
        ans.add(new int[]{l, r});  // 将最后一组区间加入答案
        return ans.toArray(new int[ans.size()][]);
    }
}

57. 插入区间

  • 思路和上一题一样
  • 把新区间加进来重新排序即可
class Solution {
    public int[][] insert(int[][] intervals, int[] newInterval) {
        int[][] res = new int[intervals.length + 1][2];
        for (int i = 0; i < intervals.length; i ++) res[i] = intervals[i];
        res[intervals.length] = newInterval;
        intervals = res;
        Arrays.sort(intervals, (o1, o2) -> o1[0] - o2[0]);
        List<int[]> ans = new ArrayList<>();
        int l = intervals[0][0], r = intervals[0][1];
        for (int i = 1; i < intervals.length; i ++) {
            // 合并操作
            if (intervals[i][0] <= r) r = Math.max(intervals[i][1], r);
            else {
                ans.add(new int[]{l, r});
                l = intervals[i][0]; r = intervals[i][1];
            }
        }
        ans.add(new int[]{l, r});  // 将最后一组区间加入答案
        return ans.toArray(new int[ans.size()][]);
    }
}

58. 最后一个单词的长度

  • 模拟
  • 找到第一个不是 的位置，然后统计即可
class Solution {
    public int lengthOfLastWord(String s) {
        int cnt = 0;
        char op = 'a';
        int idx = s.length() - 1;
        while (idx >= 0 && s.charAt(idx) == ' ') idx --;
        while (idx >= 0) {
            op = s.charAt(idx);
            if ((op >= 'a' && op <= 'z') || (op >= 'A' && op <= 'Z')) cnt ++;
            else return cnt;
            idx --;
        }
        return cnt;
    }
}

59. 螺旋矩阵 II

  • 54 青春版
  • 甚至还不需要开 vis
class Solution {
    public int[][] generateMatrix(int n) {
        int[] dx = {0, 1, 0, -1}, dy = {1, 0, -1, 0};
        int l = 0, r = 0, d = 0;
        int[][] ans = new int[n][n];
        for (int i = 1; i <= n * n; i ++) {
            ans[l][r] = i;
            int x = l + dx[d], y = r + dy[d];
            if (x < 0 || y < 0 || x >= n || y >= n || ans[x][y] != 0) {
                d = (d + 1) % 4;
                x = l + dx[d]; y = r + dy[d];
            }
            l = x; r = y;
        }
        return ans;
    }
}

60. 排列序列

  • 全排列
class Solution {
    public String getPermutation(int n, int k) {
        char[] nums = new char[n];
        for (int i = 0; i < n; i ++) nums[i] = (char)(i + 1 + '0');
        while (k -- > 1) nextPermutation(nums);
        return String.valueOf(nums);
    }

    public void nextPermutation(char[] nums) {
        int n = nums.length;
        int i = n - 2;
        while (i >= 0 && nums[i] >= nums[i + 1]) i --;
        if (i >= 0) {
            int j = n - 1;
            while (nums[j] <= nums[i]) j --;
            swap(nums, i, j);
        }
        reverse(nums, i + 1, n - 1);
    }

    private void swap(char[] nums, int i, int j) {
        char t = nums[i];
        nums[i] = nums[j];
        nums[j] = t;
    }

    private void reverse(char[] nums, int l, int r) {
        while (l < r) {
            this.swap(nums, l, r);
            l ++; r --;
        }
    }

}
DFSDP二分区间合并单调栈哈希表快速幂排列贪心
暂无评论

发送评论 编辑评论 


				

			

						

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
							
													

					

				

			

			
			

				

					
				

			

				

											

							
							
						

																

							
							
						

																

							
							
						

										
					
											
						

	

		
|´・ω・)ノ
ヾ(≧∇≦*)ゝ
(☆ω☆)
（╯‵□′）╯︵┴─┴
￣﹃￣
(/ω＼)
∠( ᐛ 」∠)＿
(๑•̀ㅁ•́ฅ)
→_→
୧(๑•̀⌄•́๑)૭
٩(ˊᗜˋ*)و
(ノ°ο°)ノ
(´இ皿இ｀)
⌇●﹏●⌇
(ฅ´ω`ฅ)
(╯°A°)╯︵○○○
φ(￣∇￣o)
ヾ(´･ ･｀｡)ノ"
( ง ᵒ̌皿ᵒ̌)ง⁼³₌₃
(ó﹏ò｡)
Σ(っ °Д °;)っ
( ,,´･ω･)ﾉ"(´っω･｀｡)
╮(╯▽╰)╭
o(*////▽////*)q
＞﹏＜
( ๑´•ω•) "(ㆆᴗㆆ)
😂
😀
😅
😊
🙂
🙃
😌
😍
😘
😜
😝
😏
😒
🙄
😳
😡
😔
😫
😱
😭
💩
👻
🙌
🖕
👍
👫
👬
👭
🌚
🌝
🙈
💊
😶
🙏
🍦
🍉
😣
Source: github.com/k4yt3x/flowerhd
	

	

		
颜文字
Emoji
小恐龙
花!
	


									

			

			
			
		

	






上一篇
下一篇 

                    

                    
			        推荐文章
		            

		            

							
Codeforces Round #807 (Div 2.) A·B·C

							
							

							
821. 跳台阶 (递归搜索树 · 一维)

							
							

							
青蛙跳

							
							

							
Codeforces Round #808 (Div 2.) A·B·C

							
							

							
Java 算竞操作

							
							

							
4219. 找倍数