756. 蛇形矩阵 (偏移量应用)

原题链接
描述：输入两个整数 n 和 m，输出一个 n 行 m 列的矩阵，将数字 1 到 n×m 按照回字蛇形填充至矩阵中。

具体矩阵形式可参考样例。

输入格式
输入共一行，包含两个整数 n 和 m。

输出格式
输出满足要求的矩阵。

矩阵占 n 行，每行包含 m 个空格隔开的整数。

数据范围
1≤n,m≤100
输入样例：

3 3

输出样例：

1 2 3
8 9 4
7 6 5

分析：

• 创建一个空的二维数组，用于存放答案
• 遍历数组，进行判断，在相应位置按递增排列

判断方法：
1.可以使用四个if else判断边界

2.记录偏移量进行判断：

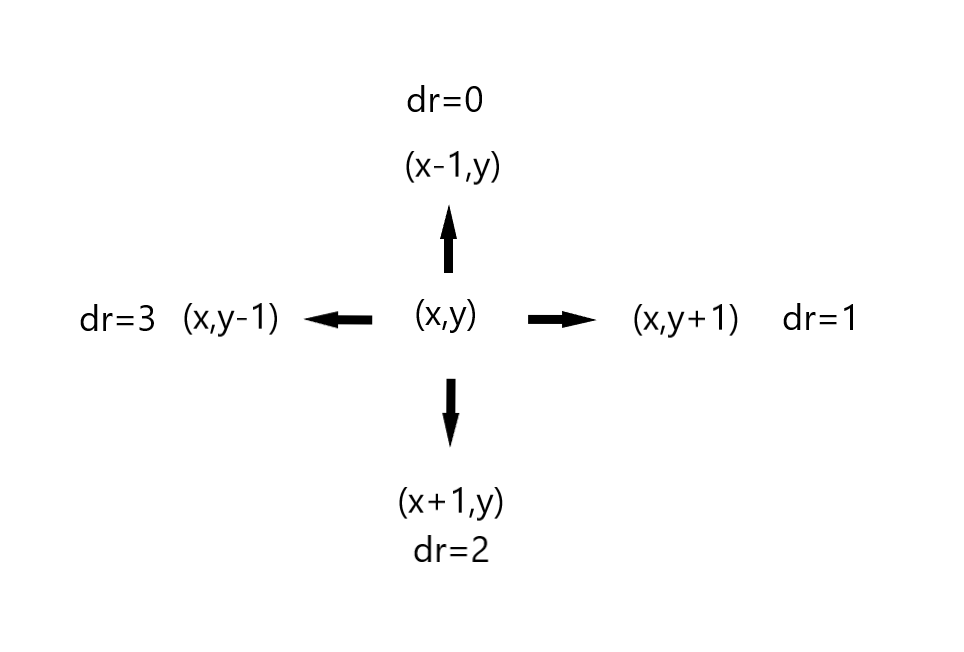
• 设当前位置坐标为(x,y)，上、下、左、右方向分别为dr=0 dr=2 dr=3 dr=1
• 则该位置上、下、左、右的位置所对应的偏移量分别为(x-1,y) (x+1,y) (x,y-1) (x,y+1)
• 将方向与偏移量的对应关系初始化为两个数组便于引用
• 
• 每次执行循环后，判断下一个位置是否到达数组边界，或数组中已经存在元素
• 若满足上述情况，则改变方向

代码

#include <bits/stdc++.h>
using namespace std;

const int maxn=110;

int a[maxn][maxn];  //定义空的二维数组数组
int dx[]={-1,0,1,0},dy[]={0,1,0,-1};  //初始化方向所对应的偏移量的数组

int main()
{
    int n,m;
    cin>>n>>m;
    int dr=1,x=0,y=0;  //初始化开始方向为右，初始化开始的位置
    for(int i=1;i<=n*m;i++){
        a[x][y]=i;  //存入答案
        int h=x+dx[dr],l=y+dy[dr];  //定义临时变量存放(x,y)的下一个位置的坐标
        if(h<0||l<0||h>=n||l>=m||a[h][l]){  //判断
            dr=(dr+1)%4;
            h=x+dx[dr],l=y+dy[dr];
        } 
        x=h,y=l;  //更新(x,y)
    }
    for(int i=0;i<n;i++){  //循环打印输出
        for(int j=0;j<m;j++){
            cout<<a[i][j]<<" ";
        }
        cout<<endl;
    }
    return 0;
}

扩展 AcWing 3208. Z字形扫描

原题链接
描述
在图像编码的算法中，需要将一个给定的方形矩阵进行 Z 字形扫描(Zigzag Scan)。

给定一个 n×n 的矩阵，Z 字形扫描的过程如下图所示：

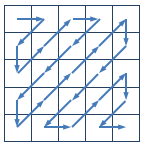
对于下面的 4×4 的矩阵，

1 5 3 9
3 7 5 6
9 4 6 4
7 3 1 3

对其进行 Z 字形扫描后得到长度为 16 的序列：1 5 3 9 7 3 9 5 4 7 3 6 6 4 1 3。

请实现一个 Z 字形扫描的程序，给定一个 n×n 的矩阵，输出对这个矩阵进行 Z 字形扫描的结果。

输入格式

输入的第一行包含一个整数 nn，表示矩阵的大小。

输入的第二行到第 n+1n+1 行每行包含 nn 个正整数，由空格分隔，表示给定的矩阵。

输出格式

输出一行，包含 n×n 个整数，由空格分隔，表示输入的矩阵经过 ZZ 字形扫描后的结果。

数据范围

1≤n≤500,
矩阵元素为不超过 1000 的正整数。

输入样例：

4
1 5 3 9
3 7 5 6
9 4 6 4
7 3 1 3

输出样例：

1 5 3 9 7 3 9 5 4 7 3 6 6 4 1 3

分析

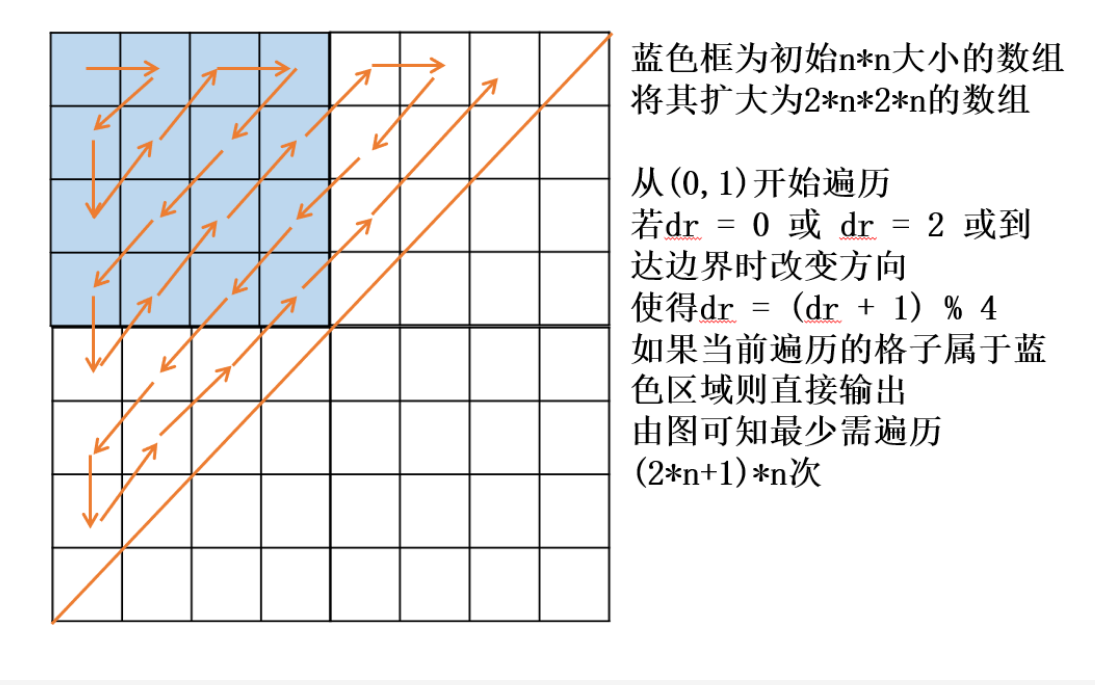
• 该题以Z字形遍历数组，对于奇数和偶数情况下，边界转向复杂
• 扩大原二维数组，使边界转向统一
• 
• 观察旋转方向，设初始方向 dr = 0
• 扩大二维数组，遍历满足在原数组范围内时输出
• 

代码

#include <bits/stdc++.h>
using namespace std;
const int N=505;

int a[2*N][2*N];  //定义时直接扩大

int main(){
    int n;
    scanf("%d",&n);
    for(int i=0;i<n;i++){  //初始化二维数组
        for(int j=0;j<n;j++){
            scanf("%d",&a[i][j]);
        }
    }
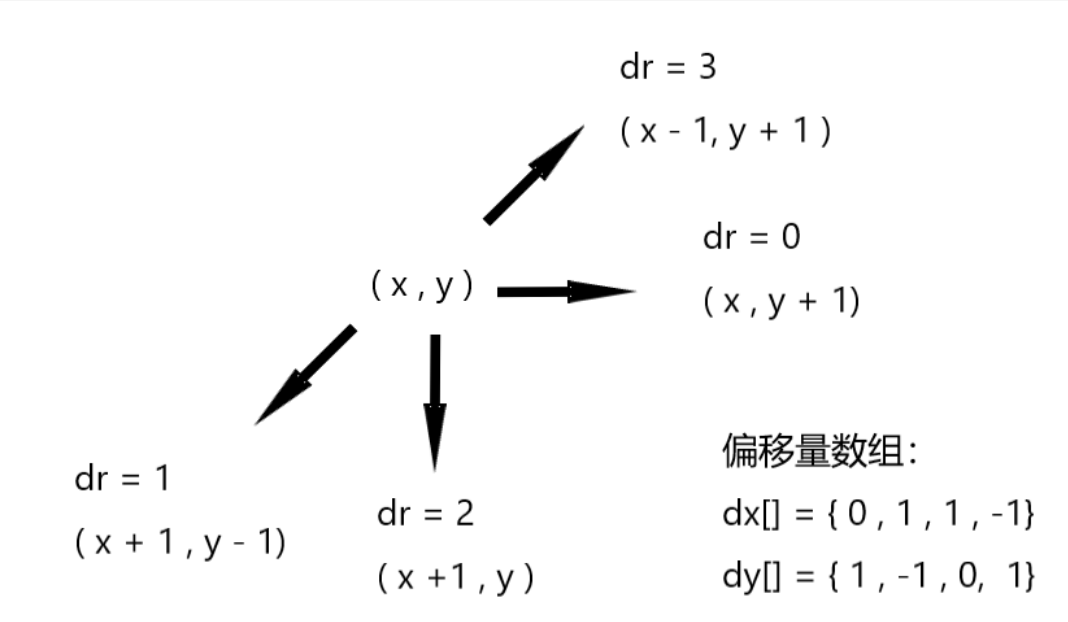
    int dr=0,dx[]={0,1,1,-1},dy[]={1,-1,0,1};  //定义(0,1)的方向dr=0  定义偏移量数组
    printf("%d ",a[0][0]);  //先将(0,0)位置的数输出
    int x=0,y=1;  //初始化位置为(0,1)
    for(int i=0;i<(2*n+1)*n;i++){  //循环遍历扩大后的数组
        if(x<n&&y<n){
            printf("%d ",a[x][y]);  //满足在原始数组范围内输出
        }
        int l=x+dx[dr],r=y+dy[dr];  //临时变量判断下一个要遍历的格子坐标(l,r)
        if(dr==0||dr==2||r<0||l<0||r>=n||l>=n){  //如果dr=0或dr=2或(l,r)出界时改变方向
            dr=(dr+1)%4;
            l=x+dx[dr],r=y+dy[dr];
        }
        x=l,y=r;  //更新(x,y)
    }
    return 0;
}