4.1 质数

概念

• 质数又称素数，一个大于$1$的自然数，除了$1$和它自身外，不能被其他自然数整除的数叫做质数；否则称为合数（规定1既不是质数也不是合数）

---

4.1.1 试除法判定质数

---

思想

• $N<2$不是质数
• 从$i=2$开始枚举，直到$\sqrt{n}$，若$i$能被$N$整除，说明不是质数
• 反之，则为质数

模板

bool is_prime(int n){

    if(n<2) return 0;  //若小于2直接返回false

    for(int i=2;i<=n/i;i++){  //优化为sqrt(n)
        if(n%i==0) return 0;
    }

    return 1;

}

---

例题 866. 试除法判定质数

原题链接

描述

给定 n 个正整数 ai，判定每个数是否是质数。

输入格式
第一行包含整数 n。

接下来 n 行，每行包含一个正整数 ai。

输出格式
共 n 行，其中第 i 行输出第 i 个正整数 ai 是否为质数，是则输出 Yes，否则输出 No。

数据范围
1≤n≤100,
1≤ai≤2^31−1
输入样例：

2
2
6

输出样例：

Yes
No

代码

#include <bits/stdc++.h>
using namespace std;

bool is_prime(int n){

    if(n<2) return 0;

    for(int i=2;i<=n/i;i++){
        if(n%i==0) return 0;
    }

    return 1;

}

int main(){

    int t;

    cin>>t;

    while(t--){

        int x;

        cin>>x;

        if(is_prime(x)) cout<<"Yes"<<endl;
        else cout<<"No"<<endl;

    }

    return 0;

}

---

4.1.2 分解质因数

---

概念

• 每个合数都可以写成几个质数相乘的形式，其中每个质数都是这个合数的因数
• 把一个合数用质因数乘积的形式表示出来，叫做分解质因数
• 如$30=2\times3\times5$ ，分解质因数只针对合数。

思想

• 算术基本定理：任何一个大于$1$的自然数$N$,如果$N$不为质数
• 那么$N$可以唯一分解成有限个质数的乘积$N=p_1^{a_1}\times p_2^{a_2}\dots\times p_i^{a_k}$,且最多只有一个大于$\sqrt{n}$的质因子
• 这里$p_1<p_2<p_3\dots p_i$均为质数，其中指数$a_k$是正整数

模板

map<int,int> primes;  //存储质因子底数和其指数的映射

void get_div(int n){

    primes.clear();  //清空数据

    for(int i=2;i<=n/i;i++){  //从2开始枚举质因子

        if(n%i==0){  //当其为质因子时
            while(n%i==0){
                primes[i]++;  //指数增加
                n/=i;
            }
        }

    }

    if(n>1) primes[n]++;  //剩余的数大于1则为最后的质因子

}

---

例题 867. 分解质因数

原题链接

描述

给定 n 个正整数 ai，将每个数分解质因数，并按照质因数从小到大的顺序输出每个质因数的底数和指数。

输入格式
第一行包含整数 n。

接下来 n 行，每行包含一个正整数 ai。

输出格式
对于每个正整数 ai，按照从小到大的顺序输出其分解质因数后，每个质因数的底数和指数，每个底数和指数占一行。

每个正整数的质因数全部输出完毕后，输出一个空行。

数据范围
1≤n≤100,
2≤ai≤2×109
输入样例：

2
6
8

输出样例：

2 1
3 1

2 3

代码

#include <bits/stdc++.h>
using namespace std;

map<int,int> primes;

void get_div(int n){

    primes.clear();

    for(int i=2;i<=n/i;i++){

        if(n%i==0){
            while(n%i==0){
                primes[i]++;
                n/=i;
            }
        }

    }

    if(n>1) primes[n]++;

}

int main(){

    int n;

    cin>>n;

    while(n--){

        int x;

        cin>>x;

        get_div(x);

        for(auto &p : primes) cout<<p.first<<" "<<p.second<<endl;

        cout<<endl;

    }

    return 0;

}

---

4.1.3 线性筛法求质数

---

思想

• 对于$1\sim N$中的一个合数$n$
• 从小到大枚举筛选出的质数$p$，将$1\sim N$范围内质数$p$的倍数的合数筛掉
• 从而保证了$n$只会被其最小质因子$p_j$筛掉，且一定会在枚举到$p_j\times\frac{n}{p_j}$之前筛掉

模板

int cnt;  //记录质数个数

int primes[N];  //存储当前筛选出的质数

bool vis[N];  //标记是否被筛掉

void get_primes(int n){

    for(int i=2;i<=n;i++){  //外层从2~n迭代

        if(!vis[i]) primes[cnt++]=i;  //没有被筛掉说明是质数，记录到primes[N]中

        for(int j=0;primes[j]<=n/i;j++){  //将1~n范围内质数primes[j]的i倍的合数筛掉
            vis[primes[j]*i]=1;  //用最小质因子primes[j]筛掉合数
            if(i%primes[j]==0) break;
            //i%primes[j]!=0 : 说明primes[j] < i的所有质因子，故primes[j]是primes[j]*i的最小质因子
            //i%primes[j]==0 : 说明从小到大枚举到此时的primes[j]，一定是i的最小质因子
        }

    }

}

---

例题 868. 筛质数

原题链接

描述

给定一个正整数 n，请你求出 1∼n 中质数的个数。

输入格式
共一行，包含整数 n。

输出格式
共一行，包含一个整数，表示 1∼n 中质数的个数。

数据范围
1≤n≤106
输入样例：

8

输出样例：

4

代码

#include <bits/stdc++.h>
using namespace std;

const int N=1e6+3;

int cnt;  //记录质数个数

int primes[N];  //存储当前筛选出的质数

bool vis[N];  //标记是否被筛掉

void get_primes(int n){

    for(int i=2;i<=n;i++){  //外层从2~n迭代

        if(!vis[i]) primes[cnt++]=i;  //没有被筛掉说明是质数，记录到primes[N]中

        for(int j=0;primes[j]<=n/i;j++){  //将1~n范围内质数primes[j]的i倍的合数筛掉
            vis[primes[j]*i]=1;  //用最小质因子primes[j]筛掉合数
            if(i%primes[j]==0) break;
            //i%primes[j]!=0 : 说明primes[j] < i的所有质因子，故primes[j]是primes[j]*i的最小质因子
            //i%primes[j]==0 : 说明从小到大枚举到此时的primes[j]，一定是i的最小质因子
        }

    }

}

int main(){

    int n;

    cin>>n;

    get_primes(n);

    cout<<cnt<<endl;

    return 0;

}

---

4.2 约数

---

概念

• 约数，又称因数。整数$a$除以整数$b(b≠0)$ 除得的商正好是整数而没有余数，我们就说$a$能被$b$整除，或$b$能整除$a$。$a$称为$b$的倍数，$b$称为$a$的约数。

---

4.2.1 试除法求约数

---

思想

• 从$i=1$开始枚举到$\sqrt{N}$
• $i$和$\frac{N}{i}$即为$N$的约数

模板

const int N=1e6+3;

int res[N];  //存储约数

int cnt;  //记录数量

void get_div(int n){

    cnt=0;  //初始化

    for(int i=1;i<=n/i;i++){  //从1开始枚举
        if(n%i==0){
            res[cnt++]=i;  //将i作为约数
            if(i!=n/i) res[cnt++]=n/i;   //将n/i作为约数
        }
    }

    sort(res,res+cnt);  //将约数从小到大排序

}

---

例题 869. 试除法求约数

原题链接

描述

给定 n 个正整数 ai，对于每个整数 ai，请你按照从小到大的顺序输出它的所有约数。

输入格式
第一行包含整数 n。

接下来 n 行，每行包含一个整数 ai。

输出格式
输出共 n 行，其中第 i 行输出第 i 个整数 ai 的所有约数。

数据范围
1≤n≤100,
2≤ai≤2×109
输入样例：

2
6
8

输出样例：

1 2 3 6 
1 2 4 8 

代码

#include <bits/stdc++.h>
using namespace std;

const int N=1e6+3;

int res[N];

int cnt;

void get_div(int n){

    cnt=0;

    for(int i=1;i<=n/i;i++){

        if(n%i==0){

            res[cnt++]=i;
            if(i!=n/i) res[cnt++]=n/i;

        }

    }

    sort(res,res+cnt);

}

int main(){

    int n;

    cin>>n;

    while(n--){

        int x;

        cin>>x;

        get_div(x);

        for(int i=0;i<cnt;i++) cout<<res[i]<<" ";

        cout<<endl;

    }

    return 0;

}

---

4.2.2 约数个数

---

思想

• 算术基本定理：任何一个大于$1$的自然数$N$,如果$N$不为质数

• 那么$N$可以唯一分解成有限个质数的乘积$N=p_1^{a_1}\times p_2^{a_2}\dots\times p_i^{a_k}$,且最多只有一个大于$\sqrt{n}$的质因子

• 这里$p_1<p_2<p_3\dots p_n$均为质数，其中指数$a_i$是正整数

• 设$d$为$N$的任意一个约数，$d=p_1^{b_1}\times p_2^{b_2}\dots\times p_i^{b_j}$，其中$0<b_j<a_k$

• 由算术基本定理可知对于$d$中的$p_i^{b_j}$项，$b_j$取值不同，则$d$不同$(每个数的因式分解是唯一的)$

• 故$N$的约数个数$=$$d$的个数$=$$b_j$的选法总数 \begin{cases} p_1共有0\sim a_1种选法\\ p_2共有0\sim a_2种选法\\ p_3共有0\sim a_3种选法\\ p_i共有0\sim a_k种选法\\ \end{cases}

• 根据乘法原理可知：$N$的约数个数为$(a_1+1)\times(a_2+1)\times(a_3+1)\times\dots\times(a_k+1)$

---

模板例题 870. 约数个数

原题链接

描述

给定 n 个正整数 ai，请你输出这些数的乘积的约数个数，答案对 109+7 取模。

输入格式
第一行包含整数 n。

接下来 n 行，每行包含一个整数 ai。

输出格式
输出一个整数，表示所给正整数的乘积的约数个数，答案需对 109+7 取模。

数据范围
1≤n≤100,
1≤ai≤2×109
输入样例：

3
2
6
8

输出样例：

12

代码

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;

const LL mod=1e9+7;

LL cnt=1;

map<int,int> primes;  //存储质因子底数和其指数的映射

void get_div(int n){

    for(int i=2;i<=n/i;i++){  //从2开始枚举质因子

        if(n%i==0){  //当其为质因子时
            while(n%i==0){
                primes[i]++;  //指数增加
                n/=i;
            }
        }

    }

    if(n>1) primes[n]++;  //剩余的数大于1则为最后的质因子

}

int main(){

    int n;

    cin>>n;

    while(n--){

        int x;

        cin>>x;

        get_div(x);

    }

    for(auto &p : primes) cnt=cnt*(p.second+1)%mod;  //核心：N的约数个数为(a1+1)*(a2+1)*(a3+1)*…*(ai+1)

    cout<<cnt<<endl;

    return 0;

}

---

4.2.3 约数之和

---

思想

• 算术基本定理：任何一个大于$1$的自然数$N$,如果$N$不为质数

• 那么$N$可以唯一分解成有限个质数的乘积$N=p_1^{a_1}\times p_2^{a_2}\dots\times p_i^{a_k}$,且最多只有一个大于$\sqrt{n}$的质因子

• 这里$p_1<p_2<p_3\dots p_i$均为质数，其中指数$a_k$是正整数

• \begin{cases} p_1的约数之和=p_1^{0}+p_1^{1}+\dots+p_1^{a_1}\\ p_2的约数之和=p_2^{0}+p_2^{1}+\dots+p_2^{a_2}\\ p_3的约数之和=p_3^{0}+p_3^{1}+\dots+p_3^{a_3}\\ ~~~~~~~~~~~~~~~~~~~~~\dots\\ p_i的约数之和=p_i^{0}+p_i^{1}+\dots+p_i^{a_k}\\ \end{cases}

• 根据乘法原理可知：$N$的约数之和$=(p_1^{0}+p_1^{1}+\dots+p_1^{a_1})\times(p_2^{0}+p_2^{1}+\dots+p_2^{a_2})\times\dots\times(p_i^{0}+p_i^{1}+\dots+p_i^{a_k})$

---

模板例题 871. 约数之和

原题链接

描述

给定 n 个正整数 ai，请你输出这些数的乘积的约数之和，答案对 109+7 取模。

输入格式
第一行包含整数 n。

接下来 n 行，每行包含一个整数 ai。

输出格式
输出一个整数，表示所给正整数的乘积的约数之和，答案需对 109+7 取模。

数据范围
1≤n≤100,
1≤ai≤2×109
输入样例：

3
2
6
8

输出样例：

252

代码

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;

const LL mod=1e9+7;

LL res=1;

map<int,int> primes;  //存储质因子底数和其指数的映射

void get_div(int n){

    for(int i=2;i<=n/i;i++){  //从2开始枚举质因子

        if(n%i==0){  //当其为质因子时
            while(n%i==0){
                primes[i]++;  //指数增加
                n/=i;
            }
        }

    }

    if(n>1) primes[n]++;  //剩余的数大于1则为最后的质因子

}

int main(){

    int n;

    cin>>n;

    while(n--){

        int x;

        cin>>x;

        get_div(x);

    }

    for(auto &p : primes){

        LL t=1;

        int a=p.first,b=p.second;

        while(b--){
            t=(t*a+1)%mod;  //核心：求出 p0一直加到p的k的次方的和
        }

        res=res*t%mod;

    }

    cout<<res<<endl;

    return 0;

}

---

4.2.4 最大公约数和最小公倍数

---

概念

• 最大公约数指两个或多个整数共有约（因）数中最大的数
• 最小公倍数指两个或多个整数的公倍数里最小的数

思想

• 辗转相除法求最大公约数

  例如：假如需要求 100 和18 两个正整数的最大公约数,用欧几里得算法，是这样进行的：
  100 / 18 = 5 (余 10)
  18 / 10= 1(余8)
  10 / 8 = 1(余2)
  8 / 2 = 4 (余0)
  至此，最大公约数为2
  以除数和余数反复做除法运算，当余数为 0 时，取当前算式除数为最大公约数，所以就得出了 100 和 18 的最大公约数2。

• 求$N$和$M$的最小公倍数$lcm(N,M)$，则先求$N$和$M$的最大公约数$gcd(N,M)$，然后$\frac{N\times M}{gcd(N,M)}$则为最小公倍数。

模板

//最大公约数
int gcd(int a, int b){
    return b ? gcd(b, a % b) : a;
}

//最小公倍数
int lcm(int a,int b){
    return a/gcd(a,b)*b;
}

---

4.3 欧拉函数

---

概念

• $1∼N$中与$N$互质的数的个数被称为欧拉函数，记为 $\phi(N)$,特别的$\phi(1)=1$
• 欧拉函数是一个积性函数，若$m$，$n$互质，则有$\phi(m\times n)=\phi(m)\times\phi(n)$

---

4.3.1 公式法求欧拉函数

---

思想

• 算术基本定理：任何一个大于$1$的自然数$N$,如果$N$不为质数

• 那么$N$可以唯一分解成有限个质数的乘积$N=p_1^{a_1}\times p_2^{a_2}\dots\times p_i^{a_k}$,且最多只有一个大于$\sqrt{n}$的质因子

• 这里$p_1<p_2<p_3\dots p_i$均为质数，其中指数$a_k$是正整数

• 则$\phi(N)=\phi(p_1^{a_1})\times\phi(p_2^{a_2})\times\dots\times\phi(p_n^{a_n})$

• 对于任意一项$\phi(p_i^{a_i})$,与$p_i^{a_i}$不互质的数有$p_i,2\times p_i,3\times p_i,\dots,p_i^{(a_i-1)}\times p_i$共$p_i^{(a_i-1)}$项

• 即$\phi(p_i^{a_i})=p_i^{a_i}-p_i^{(a_i-1)}$

• \begin{aligned} \phi(N)&=\phi(p_1^{a_1})\times\phi(p_2^{a_2})\times\dots\times\phi(p_n^{a_n})\\ &=(p_1^{a_1}-p_1^{(a_1-1)})\times(p_2^{a_2}-p_2^{(a_2-1)})\times\dots\times(p_n^{a_n}-p_n^{(a_n-1)})\\ &=p_1^{a_1}\times p_2^{a_2}\times\dots\times p_n^{a_n}\times(1-\frac{1}{p_1})\times(1-\frac{1}{p_2})\times\dots\times(1-\frac{1}{p_n})\\ &=N\times\prod^{n}_{i=1}{(1-\frac{1}{p_i})} \end{aligned}

模板

typedef long long LL;

LL phi(LL n){

    LL res=n;

    for(int i=2;i<=n/i;i++){

        if(n%i==0){
            res=res/i*(i-1);  //(1-1/i)转换为(i-1)/i
            while(n%i==0) n/=i;
        }

    }

    if(n>1) res=res/n*(n-1);

    return res;

}

---

例题 873. 欧拉函数

原题链接

描述

给定 n 个正整数 ai，请你求出每个数的欧拉函数。

欧拉函数的定义
1∼N 中与 N 互质的数的个数被称为欧拉函数，记为 ϕ(N)。
若在算数基本定理中，N=pa11pa22…pamm，则：
ϕ(N) = N×p1−1p1×p2−1p2×…×pm−1pm

输入格式
第一行包含整数 n。

接下来 n 行，每行包含一个正整数 ai。

输出格式
输出共 n 行，每行输出一个正整数 ai 的欧拉函数。

数据范围
1≤n≤100,
1≤ai≤2×109
输入样例：

3
3
6
8

输出样例：

2
2
4

代码

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;

LL phi(LL n){

    LL res=n;

    for(int i=2;i<=n/i;i++){

        if(n%i==0){
            res=res/i*(i-1);
            while(n%i==0) n/=i;
        }

    }

    if(n>1) res=res/n*(n-1);

    return res;

}

int main(){

    int n;

    cin>>n;

    while(n--){

        int x;

        cin>>x;

        cout<<phi(x)<<endl;

    }

    return 0;

}

---

4.3.2 筛法求欧拉函数

---

思想

• 利用线性筛，在筛选$1\sim N$中的质数时，将$1\sim N$的欧拉函数$\phi(P_i)$求出
• 对于质数$P_i$,其$\phi(P_i)=P\times(1-\frac{1}{P})=P-1$
• 对于合数$P_i$,其\phi(P_i)=N\times\prod^{n}_{i=1}{(1-\frac{1}{p_i})}
• 在线性筛法求质数的模板中利用最小质因子筛掉合数的过程时：
  • 当$i\%primes[j]=0$时，说明$primes[j]$是$i$的一个质因子，且$primes[j]$是$primes[j]\times i$的一个质因子，故$\phi(i)$包含$(1-\frac{1}{primes[j]})$的情况，即$\phi(primes[j]\times i)=primes[j]\times\phi(i)$
  • 当$i\%primes[j]\ne 0$时 ，说明$primes[j]$是$i$的最小质因子，且$primes[j]$不是$primes[j]\times i$的一个质因子，故$\phi(i)$不包含$(1-\frac{1}{primes[j]})$的情况，即$\begin{aligned}\phi(primes[j]\times i)&=primes[j]\times\phi(i)\times(1-\frac{1}{primes[j]})\ &=(primes[j]-1)\times\phi(i)\end{aligned}$

模板

int primes[N];   //存储当前筛选出的质数

bool vis[N];  //标记是否被筛掉

int phi[N]; //记录欧拉函数的值

int cnt;  //记录质数个数

void get_phi(int n){

    phi[1]=1;  //特别的，phi[1]=1

    for(int i=2;i<=n;i++){

        if(!vis[i]){
            primes[cnt++]=i;  //没有被筛掉说明是质数，记录到primes[N]中
            phi[i]=i-1;  //质数的欧拉函数的情况
        }

        for(int j=0;primes[j]<=n/i;j++){  //将1~n范围内质数primes[j]的i倍的合数筛掉

            vis[primes[j]*i]=1;
            if(i%primes[j]==0){  //用最小质因子primes[j]筛掉合数
                phi[primes[j]*i]=primes[j]*phi[i];  //包含(1-1/primes[j])的情况
                break;
            }
            else phi[primes[j]*i]=(primes[j]-1)*phi[i];  //不包含(1-1/primes[j])的情况

        }

    }

}

---

例题 874. 筛法求欧拉函数

原题链接

描述

给定一个正整数 n，求 1∼n 中每个数的欧拉函数之和。

输入格式
共一行，包含一个整数 n。

输出格式
共一行，包含一个整数，表示 1∼n 中每个数的欧拉函数之和。

数据范围
1≤n≤106
输入样例：

6

输出样例：

12

代码

#include <bits/stdc++.h>
using namespace std;

const int N=1e6+3;

typedef long long LL;

int primes[N];

bool vis[N];

int phi[N];

int cnt;

void get_phi(int n){

    phi[1]=1;

    for(int i=2;i<=n;i++){

        if(!vis[i]){
            primes[cnt++]=i;
            phi[i]=i-1;
        }

        for(int j=0;primes[j]<=n/i;j++){

            vis[primes[j]*i]=1;
            if(i%primes[j]==0){
                phi[primes[j]*i]=primes[j]*phi[i];
                break;
            }
            else phi[primes[j]*i]=(primes[j]-1)*phi[i];

        }

    }

}

int main(){

    int n;

    cin>>n;

    get_phi(n);

    LL res=0;

    for(int i=1;i<=n;i++){
        res+=phi[i];
    }

    cout<<res<<endl;

    return 0;

}

---

4.4 快速幂

---

概念

• 快速求出$a^k\mod p$的结果

思想

• 预处理出$a^{2^0},a^{2^1},a^{2^2}\dots a^{2^{log_2^k}}$的结果
• 则使得$k=2^{p_1}+2^{p_2}+\dots+2^{p_i}$
• 即：$a^k=a^{2^{p_1}}\times a^{2^{p_2}}\times\dots\times a^{2^{p_i}}$
• 对于$a^{2^0}\times a^{2^0}=a^{2^{1}},a^{2^{1}}\times a^{2^{1}}=a^{2^{2}}$，即a^{2^{p_i}}=a^{2^{p_{i-1}}}\times a^{2^{p_{i-1}}}
• 综上所述，在操作时记录$a^{p_i}$的值，和累乘的结果
• 将$k$化为二进制表示，按位>>操作，若当前位是$1$，则对当前累乘的结果$\times a^{p_i} \mod p$
• 每次对k进行按位>>操作后，更新a^{p_{i+1}}=a^{p_i}\times a^{p_i}\mod p
• 当二进制下的$k$无法再>>时，累乘结果即为答案

模板

typedef long long LL;

LL qmi(LL a,LL k,LL p){  //计算 a^k % p 的结果

    LL res=1;  //记录累乘结果

    while(k){

        if(k&1) res=res*a%p;  //k&1得到当前位，若为1则累乘a^pi
        a=a*a%p;  //更新a^pi
        k>>=1;  //右移1位
    }

    return res;

}

---

4.4.1 快速幂求逆元

---

概念

• 同余：设$m$为正整数，$a$和$b$是整数，若$m|a-b$，则称$a$模$m$同余于$b$，或$a$与$b$模$m$同余，记作$a\equiv b(mod~m)$
• 若$ab\equiv 1(mod~m)$，则称$b$为$a$的模$m$逆，记作$a^{-1}(mod~m)$或$a^{-1}$

注意

• $a$的模$m$逆存在 $\Leftrightarrow$ $a$与$m$互质

• 当$m$为质数时，用费马小定理求

• 当$m$不为质数时，用扩展欧几里得算法求

思想

• 利用快速幂实现$m$为质数时用费马小定理求逆元

• 费马小定理：设$p$为素数，且$a$与$p$互质，则$a^{p^{-1}}\equiv 1(mod~p)$

• \begin{aligned} a^{p^{-1}}\equiv 1(mod~p) \rightarrow &a\times a^{p^{-2}}\equiv 1(mod~p)\\ &a\times b\equiv 1(mod~p)\\ &即：b=a^{p^{-2}} \end{aligned}

---

模板例题 876. 快速幂求逆元

原题链接

描述

给定 n 组 ai,pi，其中 pi 是质数，求 ai 模 pi 的乘法逆元，若逆元不存在则输出 impossible。

注意：请返回在 0∼p−1 之间的逆元。

乘法逆元的定义
若整数 b，m 互质，并且对于任意的整数 a，如果满足 b|a，则存在一个整数 x，使得 a/b≡a×x(modm)，则称 x 为 b 的模 m 乘法逆元，记为 b−1(modm)。
b 存在乘法逆元的充要条件是 b 与模数 m 互质。当模数 m 为质数时，bm−2 即为 b 的乘法逆元。

输入格式
第一行包含整数 n。

接下来 n 行，每行包含一个数组 ai,pi，数据保证 pi 是质数。

输出格式
输出共 n 行，每组数据输出一个结果，每个结果占一行。

若 ai 模 pi 的乘法逆元存在，则输出一个整数，表示逆元，否则输出 impossible。

数据范围
1≤n≤105,
1≤ai,pi≤2∗109
输入样例：

3
4 3
8 5
6 3

输出样例：

1
2
impossible

代码

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;

LL qmi(LL a,LL k,LL p){

    LL res=1;

    while(k){

        if(k&1) res=res*a%p;
        a=a*a%p;
        k>>=1;

    }

    return res;

}

int main(){

    int n;

    cin>>n;

    while(n--){

        int a,p;

        cin>>a>>p;

        if(a%p==0) cout<<"impossible"<<endl;  //a与p不互质则说明无逆元
        else cout<<qmi(a,p-2,p)<<endl;

    }

    return 0;

}

---

4.5 扩展欧几里得算法

---

思想

• 欧几里得算法：$gcd(a,b)=gcd(b,a\%b)$，特别的$gcd(a,0)=a$

• 裴蜀定理：对于任意正整数$a,b$，一定存在非零的$x,y$，使得$ax+by=gcd(a,b)$

• \begin{cases} b=0时:\begin{cases} gcd(a,b)=a\\ax+by=gcd(a,b)\\ \end{cases}\Rightarrow\begin{cases}x=1\\y=0\end{cases} \\ \\ \\ \\ \\ b\neq0时： \begin{cases} \begin{aligned} ①&设~ax+by=gcd(a,b)=d\\ &\because 由欧几里得算法可知：gcd(a,b)=gcd(b,a\%b)=d\\ &\therefore 由裴蜀定理得：b{x}'+(a\%b){y}'=d\\ 又&\because ax+by=d\\ &\therefore联立 \begin{cases} ax+by=d\\b{x}'+(a\%b){y}'=d\\a\%b=a-\lfloor\frac{a}{b}\rfloor b \end{cases}\Rightarrow\begin{cases}x={y}'\\y={x}'-\lfloor\frac{a}{b}\rfloor{y}'\end{cases}\\ ②&设{a}'=b,{b}'=a\%b\\ &\therefore gcd(b,a\%b)=gcd({a}',{b}')=d\\ &\because gcd({a}',{b}')=gcd({b}',{a}'\%{b}')=d\\ &\therefore {b}'{x}''+{a}'\%{b}'{y}''=d\\ 又&\because b{x}'+(a\%b){y}'=d\\ &\therefore联立\begin{cases} b{x}'+(a\%b){y}'=d\\{b}'{x}''+{a}'\%{b}'{y}''=d\\{a}'\%{b}'={a}'-\lfloor\frac{{a}'}{{b}'}\rfloor{b}' \end{cases}\Rightarrow\begin{cases}{x}'={y}''\\{y}'={x}''-\lfloor\frac{{a}'}{{b}'}\rfloor{y}'' \end{cases}\\ ③&设{a}''={b}',{b}''={a}'\%{b}'\\ &\dots\\ &\dots\\ &直到b=0时，联立解得\begin{cases}{x}^i=1\\{y}^i=0\end{cases}\\ &然后逐步返回每一次联立所得的结果\begin{cases}{x}^{i-1}={y}^{i}\\{y}^{i-1}={x}^{i}-\lfloor\frac{{a}^{i}}{{b}^i}\rfloor{y}^{i} &最后返回得到x和y的值 \end{cases}\\ \end{aligned} \end{cases} \end{cases}

注意

• 当方程符合$ax+by=gcd(a,b)$的形式时，才可以用扩展欧几里得算法求解$(x_0,y_0)$

• 推论：可以进一步求解任意方程$ax+by=n$，得到一个整数解

• \begin{aligned} \begin{cases} &(1)~~判断方程ax+by=n是否有整数解，有解的条件为：gcd(a,b)可以整除n\\ &(2)~~用扩展欧几里得算法求ax+by=gcd(a,b)得到一个解(x_0,y_0)\\ &(3)~~在ax_0+by_0=gcd(a,b)两边同时乘\frac{n}{gcd(a,b)}\Rightarrow\frac{ax_0n}{gcd(a,b)}+\frac{by_0n}{gcd(a,b)}=n\\ &(4)~~对照ax+by=n可知该方程的一个解为({x}',{y}')，其中\begin{cases}{x}'=\frac{x_0n}{gcd(a,b)}\\{y}'=\frac{y_0n}{gcd(a,b)} \end{cases} \end{cases} \end{aligned}

模板

void exgcd(int a,int b,int &x,int &y){

    if(!b){  //若b=0时
        x=1,y=0;
        return ;
    }
    else{  //b!=0时
        exgcd(b,a%b,x,y);  //递归到下一层
        int t=x;  //返回时执行
        x=y;
        y=t-a/b*y;
    }

}

---

例题 877. 扩展欧几里得算法

原题链接

描述

给定 n 对正整数 ai,bi，对于每对数，求出一组 xi,yi，使其满足 ai×xi+bi×yi=gcd(ai,bi)。

输入格式
第一行包含整数 n。

接下来 n 行，每行包含两个整数 ai,bi。

输出格式
输出共 n 行，对于每组 ai,bi，求出一组满足条件的 xi,yi，每组结果占一行。

本题答案不唯一，输出任意满足条件的 xi,yi 均可。

数据范围
1≤n≤105,
1≤ai,bi≤2×109
输入样例：

2
4 6
8 18

输出样例：

-1 1
-2 1

代码

#include <bits/stdc++.h>
using namespace std;

void exgcd(int a,int b,int &x,int &y){

    if(!b){

        x=1,y=0;
        return ;

    }
    else{

        exgcd(b,a%b,x,y);

        int t=x;

        x=y;

        y=t-a/b*y;

    }

}

int main(){

    int n;

    cin>>n;

    while(n--){

        int a,b,x,y;

        cin>>a>>b;

        exgcd(a,b,x,y);

        cout<<x<<" "<<y<<endl;

    }

    return 0;

}

---

4.5.1 解一元线性同余方程

---

概念

• $ax\equiv b(mod~m)$，即$\frac{ax}{m}$与$\frac{b}{m}$的余数相同，且$a,b,m$为整数，求$x$的值
• 该方程即为一元线性同余方程

思想

• 对$ax\equiv b(mod~m)$做等价变形：$ax+my=b$

• \begin{aligned} &\because &ax&\equiv b(mod~m)\\ &\therefore &ax\%m&=k(b\%m),(k\in \Z)\\ &\therefore &ax-\lfloor\frac{ax}{m}\rfloor m&=k(b-\lfloor\frac{b}{m}\rfloor m)\\ &\therefore &ax-kb&=(\lfloor\frac{ax}{m}\rfloor-k\lfloor\frac{b}{m}\rfloor)m\\ &\because &\lfloor\frac{ax}{m}\rfloor,&\lfloor\frac{b}{m}\rfloor,k\in \Z\\ &\therefore &(\lfloor\frac{ax}{m}\rfloor&-k\lfloor\frac{b}{m}\rfloor)\in \Z\\ &&设(\lfloor\frac{ax}{m}\rfloor&-k\lfloor\frac{b}{m}\rfloor)=y,(y\in \Z)\\ &\therefore &ax-kb&=my\Rightarrow ax-my=b\\ 又&\because &y&可以为负数\\ &\therefore &ax\equiv b(mod~&m)\leftrightarrow ax+my=b \end{aligned}

• 由扩展欧几里得算法的推论可知：当且仅当$ gcd(a,m)$可以整除$b$时，$ax+my=b$存在整数解

• 由扩展欧几里得算法可知： \begin{cases} 当gcd(a,m)=b时：\begin{cases}x=x_0\\y=y_0\end{cases}\\ 当gcd(a,m)为b的整数倍时：\begin{cases}{x}'=\frac{x_0b}{gcd(a,m)}\\{y}'=\frac{y_0b}{gcd(a,m)}\end{cases} \end{cases}

---

例题 878. 线性同余方程

原题链接

描述

给定 n 组数据 ai,bi,mi，对于每组数求出一个 xi，使其满足 ai×xi≡bi(modmi)，如果无解则输出 impossible。

输入格式
第一行包含整数 n。

接下来 n 行，每行包含一组数据 ai,bi,mi。

输出格式
输出共 n 行，每组数据输出一个整数表示一个满足条件的 xi，如果无解则输出 impossible。

每组数据结果占一行，结果可能不唯一，输出任意一个满足条件的结果均可。

输出答案必须在 int 范围之内。

数据范围
1≤n≤105,
1≤ai,bi,mi≤2×109

2
2 3 6
4 3 5

输出样例：

输出样例：

impossible
-3

代码

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;

void exgcd(LL a,LL b,LL &x,LL &y){

    if(!b){  //若b=0时
        x=1,y=0;
        return ;
    }
    else{
        exgcd(b,a%b,x,y);
        LL t=x;
        x=y;
        y=t-a/b*y;
    }

}

LL gcd(LL a,LL b){
    return b ? gcd(b,a%b) : a;
}

int main(){

    int n;

    cin>>n;

    while(n--){

        LL a,b,m,x,y;

        cin>>a>>b>>m;

        LL d=gcd(a,m);

        exgcd(a,m,x,y);

        if(b%d) cout<<"impossible"<<endl;
        else cout<<b/d*x%m<<endl;

    }

    return 0;

}

---

4.6 中国剩余定理

---

概念

• 若存在整数$m_1,m_2,m_3\dots m_n$两两互质，则对于任意的整数$a_1,a_2,a_3\dots a_n$，一元线性同余方程组$(S)$有通解

• (S): \begin{cases} x\equiv a_1(mod~m_1)\\ x\equiv a_2(mod~m_2)\\ x\equiv a_3(mod~m_3)\\ \dots\\ x\equiv a_n(mod~m_n)\\ \end{cases}

思想

• 对于$(S)$其中的两个式子进行合并

• \begin{cases} x\equiv a_1(mod~m_1)\\ x\equiv a_2(mod~m_2)\\ \end{cases} \Rightarrow \begin{cases} x=k_1m_1+a_1\\ x=k_2m_2+a_2\\ \end{cases}

• 将等价转换后的两式进行联立，化简得$k_1m_1+k_2(-m_2)=a_2-a_1~①$

• 由扩展欧几里得算法可以得到一组解$({k_1}',{k_2}')$，使得：${k_1}'m_1+{k_2}'(-m_2)=gcd(m_1,-m_2)$

• 若$gcd(m_1,-m_2)$不能整除$a2-a1$，则无解，否则有通解

• 设$gcd(m_1,-m_2)=d,y=\frac{(a_2-a_1)}{d}$

• 由扩展欧几里得算法的推论可知：\begin{cases}k_1={k_1}'y\\k_2={k_2}'y\end{cases}

• 引入通解\begin{cases}k_1={k_1}+k\frac{m_2}{d}\\k_2={k_2}+\frac{m_1}d\end{cases}，$k\in \Z$

• 将通解带入$①$得$({k_1}+k\frac{m_2}{d})m_1+({k_2}+k\frac{m_1}{d})(-m_2)=a_2-a_1$

• 化简得$k_1m_1+k_2(-m_2)=a_2-a_1$和$①$相同，故成立

• 重复上述步骤，不断合并剩余的式子，即可得到最终的通解

---

例题 204. 表达整数的奇怪方式

原题链接

描述

给定 2n 个整数 a1,a2,…,an 和 m1,m2,…,mn，求一个最小的非负整数 x，满足 ∀i∈[1,n],x≡mi(mod ai)。

输入格式
第 1 行包含整数 n。

第 2…n+1 行：每 i+1 行包含两个整数 ai 和 mi，数之间用空格隔开。

输出格式
输出最小非负整数 x，如果 x 不存在，则输出 −1。
如果存在 x，则数据保证 x 一定在 64 位整数范围内。

数据范围
1≤ai≤231−1,
0≤mi<ai
1≤n≤25
输入样例：

2
8 7
11 9

输出样例：

31

代码

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;

void exgcd(LL a,LL b, LL &x,LL &y){

    if(!b){

        x=1,y=0;
        return ;

    }
    else{
        exgcd(b,a%b,x,y);
        LL t=x;
        x=y;
        y=t-a/b*y;
    }

}

LL gcd(LL a,LL b){
    return b ? gcd(b,a%b) : a;
}

int main(){

    int n;

    cin>>n;

    LL x=0,m1,a1;  //第一个方程的系数 备份数据

    cin>>m1>>a1;  //先输入第一个方程

    for(int i=0;i<n-1;i++){  //合并接下来的n-1个方程

        LL m2,a2;

        cin>>m2>>a2;

        LL k1,k2;

        LL d=gcd(m1,m2);

        exgcd(m1,m2,k1,k2);

        if((a2-a1)%d){  //此时无解

            x=-1;
            break;

        }

        k1*=(a2-a1)/d;//特解
        k1=(k1%(m2/d)+m2/d)%(m2/d);  //让特解k1取到最小正整数解

        x=k1*m1+a1;

        LL m=abs(m1/d*m2);
        a1=k1*m1+a1;  

        m1=m;

    }

    if(x!=-1) x=(a1%m1+m1)%m1   //当循环结束时，此时的值应该与最小公倍数取模,以求得最小正整数解

    cout<<x<<endl;

    return 0;

}

---

4.7 高斯消元

---

概念

• 利用初等行（列）变换，对一组线性方程组进行消元，把增广矩阵化为阶梯型矩阵

• \begin{aligned} 已知某线&性方程组：\\\\ &\begin{cases} a_{11}x_1+a_{12}x_2+\dots+a_{1n}x_n=b_1\\ a_{21}x_1+a_{22}x_2+\dots+a_{2n}x_n=b_2\\ \dots\\ a_{n1}x_1+a_{n2}x_2+\dots+a_{nn}x_n=b_n\\ \end{cases}\\\\ 增广矩阵&为：\\\\ &\begin{pmatrix} a_{11}&a_{12}&\dots&a_{1n}&b_1\\ a_{21}&a_{22}&\dots&a_{2n}&b_2\\ \vdots&\vdots&\vdots&\vdots&\vdots\\ a_{n1}&a_{n2}&\dots&a_{nn}&b_n\\ \end{pmatrix}\\\\ 运用初等&行变换：\\\\ &\begin{pmatrix} a_{11}&a_{12}&\dots&a_{1n}&b_1\\ &a_{22}&a_{2(i+1)}&a_{2n}&b_2\\ &&&\vdots&\vdots\\ &&&a_{nn}&b_n\\ \end{pmatrix}\\\\ \end{aligned}\\ 解的情况 \begin{cases} 无解:若在最后化成的上三角形矩阵中,正对角线中某个元素为0,\\但其所在行的最后一列元素不为0时,此时矩阵无解\\\\有无数解:若在最后化成的上三角形矩阵中,\\存在正对角线中某个元素为0,\\且其所在行的最后一列元素也为0时,\\此时矩阵有无穷组解 \\\\有唯一解:若在最后化成的上三角形矩阵中,不存在正对角线中某个元素为0,\\此时矩阵有唯一解\\ \end{cases}

初等行（列）变换

• 某一行乘上一个非零数，矩阵不变
• 某一行乘上一个常数加到另一行上，矩阵不变
• 交换矩阵中某两行的元素，矩阵不变

思想

• 对增广矩阵的每一列$c_i$进行枚举，找到当前的列中绝对值最大的元素所在的行$r_i$
• 将$r_i$行与最上方未确定阶梯型的行进行交换
• 用初等行变换将$r_i$行变为原来的$k$倍，且使得变换后， $r_i$行的第一个数变成$1$
• 继续用初等行变换，将$r_i$行下方的所有的行的$c_i$列的值变为$0$
• 重复上述步骤，直到最终得到阶梯型矩阵，判断解的情况
• 若有解，则从最后一行向上回代，得出方程组的解

模板

const int N=110;

const double eps=1e-8;

int n;

double a[N][N];

int gauss(){

    int c,r;

    for (c=0,r=0;c<n;c++){

        int t=r;

        for(int i=r;i<n;i++){  //筛选出所在列元素最大的行
            if(fabs(a[i][c])>fabs(a[t][c])) t=i;
        }

        if(fabs(a[t][c])<eps) continue;  //正对角线中有元素为0,这时有无穷解和无解

        if(t!=r) for(int i=c;i<=n;i++) swap(a[t][i],a[r][i]);  //若t改变，则交换两行

        for(int i=n;i>=c;i--) a[r][i]/=a[r][c];  //将所在行所在列元素变为1

        for(int i=r+1;i<n;i++){  //将所在行所在列的下方的行的所在列元素变为0
            if(fabs(a[i][c])>eps){
                for(int j=n;j>=c;j--) a[i][j]-=a[r][j]*a[i][c];
            }
        }

        r++;

    }

    if(r<n){  //row<n,即对角线中元素为0的行未被算上
        for(int i=r;i<n;i++){
            if(fabs(a[i][n])>eps) return 2;
        }
        return 1;
    }

    for(int i=n-1;i>=0;i--){  //将非主元位置的A系数矩阵的其他x消去
        for(int j=i+1;j<n;j++) a[i][n]-=a[j][n]*a[i][j];
    }

    return 0;

}

---

4.7.1 高斯消元解线性方程组

---

模板例题 883. 高斯消元解线性方程组

原题链接

描述

输入一个包含 n 个方程 n 个未知数的线性方程组。

方程组中的系数为实数。

求解这个方程组。

下图为一个包含 m 个方程 n 个未知数的线性方程组示例：

\begin{cases} a_{11}x_1+a_{12}x_2+\dots+a_{1n}x_n=b_1\\ a_{21}x_1+a_{22}x_2+\dots+a_{2n}x_n=b_2\\ \dots\\ a_{m1}x_1+a_{m2}x_2+\dots+a_{mn}x_n=b_n\\ \end{cases}\\\\
输入格式
第一行包含整数 n。

接下来 n 行，每行包含 n+1 个实数，表示一个方程的 n 个系数以及等号右侧的常数。

输出格式
如果给定线性方程组存在唯一解，则输出共 n 行，其中第 i 行输出第 i 个未知数的解，结果保留两位小数。

如果给定线性方程组存在无数解，则输出 Infinite group solutions。

如果给定线性方程组无解，则输出 No solution。

数据范围
1≤n≤100,
所有输入系数以及常数均保留两位小数，绝对值均不超过 100。

输入样例：

3
1.00 2.00 -1.00 -6.00
2.00 1.00 -3.00 -9.00
-1.00 -1.00 2.00 7.00

输出样例：

1.00
-2.00
3.00

分析
\begin{aligned} 由样例可&得增广矩阵：\\\\ &\begin{pmatrix} 1&2&-1&-6\\ 2&1&-3&-9\\ -1&-1&2&7\\ \end{pmatrix}\\\\c_1中绝对&值最大元素位于r_2，将r_2与r_1交换：\\\\ &\begin{pmatrix} 2&1&-3&-9\\ 1&2&-1&-6\\ -1&-1&2&7\\ \end{pmatrix}\\\\ 将r_1的第&c_1列元素变为1，需要使得r_1\times \frac{1}{2}:\\\\ &\begin{pmatrix} 1&0.5&-1.5&-4.5\\ 1&2&-1&-6\\ -1&-1&2&7\\ \end{pmatrix}\\\\ 利用初等&行变换将r_1下方的所有的行的c_1列变为0:\\ &即执行r_2-r_1、r_3+r_1\\\\ &\begin{pmatrix} 1&0.5&-1.5&-4.5\\ 0&1.5&0.5&-1.5\\ 0&-0.5&0.5&2.5\\ \end{pmatrix}\\\\ 此时r_1已&确定为阶梯矩阵的行，从r_1下方继续枚举,\\ c_2中绝对&值最大的元素位于r_2，由于r_2上方无未确\\ 定的阶梯&矩阵的行，故不需要交换。\\ 将r_2的第&c_2列元素变为1，需要使得r_2\times \frac{2}{3}:\\\\ &\begin{pmatrix} 1&0.5&-1.5&-4.5\\ 0&1&\frac{1}{3}&-1\\ 0&-0.5&0.5&2.5\\ \end{pmatrix}\\\\ 利用初等&行变换将r_2下方的所有的行的c_2列变为0:\\ &即执行r_3+r_2\times\frac{1}{2}\\\\ &\begin{pmatrix} 1&0.5&-1.5&-4.5\\ 0&1&\frac{1}{3}&-1\\ 0&0&\frac{2}{3}&2\\ \end{pmatrix}\\\\ 此时r_2已&确定为阶梯矩阵的行，从r_2下方继续枚举,\\ r_3为最后&一行，将r_3的第c_3列元素变为1，需要使得r_3\times \frac{3}{2}:\\\\ &\begin{pmatrix} 1&0.5&-1.5&-4.5\\ 0&1&\frac{1}{3}&-1\\ 0&0&1&3\\ \end{pmatrix}\\\\ 判断该上&三角矩阵中不存在正对角线中某个元素为0,此时\\ 矩阵有唯&一解，x_3=3,从r_2进行回代:\\ &即执行r_2-r_3\times\frac{1}{3}\\\\ &\begin{pmatrix} 1&0.5&-1.5&-4.5\\ 0&1&0&-2\\ 0&0&1&3\\ \end{pmatrix}\\\\ 此时可得&x_2=-2,回代r_1:\\ &即执行r_1-r_2\times\frac{1}{2}+r_3\times\frac{3}{2}\\\\ &\begin{pmatrix} 1&0&0&1\\ 0&1&0&-2\\ 0&0&1&3\\ \end{pmatrix}\\\\ 此时可得&x_1=1,综上可得: \begin{cases} x_1=1\\x_2=-2\\x_3=3 \end{cases} \end{aligned}

代码

#include <bits/stdc++.h>
using namespace std;

const int N=110;

const double eps=1e-8;

int n;

double a[N][N];

int gauss(){

    int c,r;

    for (c=0,r=0;c<n;c++){

        int t=r;

        for(int i=r;i<n;i++){  //筛选出所在列元素最大的行
            if(fabs(a[i][c])>fabs(a[t][c])) t=i;
        }

        if(fabs(a[t][c])<eps) continue;  //正对角线中有元素为0,这时有无穷解和无解

        if(t!=r) for(int i=c;i<=n;i++) swap(a[t][i],a[r][i]);  //若t改变，则交换两行

        for(int i=n;i>=c;i--) a[r][i]/=a[r][c];  //将所在行所在列元素变为1

        for(int i=r+1;i<n;i++){  //将所在行所在列的下方的行的所在列元素变为0
            if(fabs(a[i][c])>eps){
                for(int j=n;j>=c;j--) a[i][j]-=a[r][j]*a[i][c];
            }
        }

        r++;

    }

    if(r<n){  //row<n,即对角线中元素为0的行未被算上
        for(int i=r;i<n;i++){
            if(fabs(a[i][n])>eps) return 2;
        }
        return 1;
    }

    for(int i=n-1;i>=0;i--){  //将非主元位置的A系数矩阵的其他x消去
        for(int j=i+1;j<n;j++) a[i][n]-=a[j][n]*a[i][j];
    }

    return 0;

}

int main(){

    cin>>n;

    for(int i=0;i<n;i++){
        for(int j=0;j<=n;j++){
            cin>>a[i][j];
        }
    }

    int t=gauss();

    if(t==2){
        cout<<"No solution"<<endl;
    }
    else if(t==1) cout<<"Infinite group solutions"<<endl;
    else{
        for(int i=0;i<n;i++){
            if(fabs(a[i][n])<eps) a[i][n]=0;
            printf("%.2lf\n",a[i][n]);
        }
    }

    return 0;

}

---

4.7.2 高斯消元解异或线性方程组

---

思想

• 将解线性方程组的计算化为异或运算

模板例题 884. 高斯消元解异或线性方程组

原题链接

描述

输入一个包含 n 个方程 n 个未知数的异或线性方程组。

方程组中的系数和常数为 0 或 1，每个未知数的取值也为 0 或 1。

求解这个方程组。

异或线性方程组示例如下：

M[1][1]x[1] ^ M[1][2]x[2] ^ … ^ M[1][n]x[n] = B[1]
M[2][1]x[1] ^ M[2][2]x[2] ^ … ^ M[2][n]x[n] = B[2]
…
M[n][1]x[1] ^ M[n][2]x[2] ^ … ^ M[n][n]x[n] = B[n]
其中 ^ 表示异或(XOR)，M[i][j] 表示第 i 个式子中 x[j] 的系数，B[i] 是第 i 个方程右端的常数，取值均为 0 或 1。

输入格式
第一行包含整数 n。

接下来 n 行，每行包含 n+1 个整数 0 或 1，表示一个方程的 n 个系数以及等号右侧的常数。

输出格式
如果给定线性方程组存在唯一解，则输出共 n 行，其中第 i 行输出第 i 个未知数的解。

如果给定线性方程组存在多组解，则输出 Multiple sets of solutions。

如果给定线性方程组无解，则输出 No solution。

数据范围
1≤n≤100
输入样例：

3
1 1 0 1
0 1 1 0
1 0 0 1

输出样例：

1
0
0

代码

#include <bits/stdc++.h>
using namespace std;

const int N=110;

int n;

int a[N][N];

int guass(){

    int c,r;

    for (c=0,r=0;c<n;c++){

        int t=r;

        for (int i=r;i<n;i++){
            if (a[i][c]) t = i;
        }

        if(!a[t][c]) continue;

        for (int i=c;i<=n;i++) swap(a[r][i],a[t][i]);

        for (int i=r+1;i<n;i++){
            if (a[i][c]){
                for (int j=n;j>=c;j--) a[i][j]^=a[r][j];
            }
        }

        r++;

    }

    if(r<n){

        for(int i=r;i<n;i++){
            if(a[i][n]) return 2;
        }

        return 1;

    }

    for(int i=n-1;i>=0;i--){
        for(int j=i+1;j<n;j++){
            a[i][n]^=a[i][j]*a[j][n];
        }
    }

    return 0;

}

int main(){

    cin>>n;

    for(int i=0;i<n;i++){
        for(int j=0;j<n+1;j++){
            cin>>a[i][j];
        }
    }

    int t=guass();

    if(t==0){

        for(int i=0;i<n;i++) cout<<a[i][n]<<endl;

    }
    else if(t==1) cout<<"Multiple sets of solutions"<<endl;
    else cout<<"No solution"<<endl;

    return 0;

}

---

4.8 组合数

---

概念

• 从$n$个不同元素中每次取出$m$个不同元素，不管其顺序合成一组，称为从$n$个元素中不重复地选取$m$个元素的一个组合。
• 所有这样的组合的种数称为组合数

公式

• $C_{n}^{m}=\frac{n!}{m!(n-m)!},C_n^0=C_n^n=1$
• $C_n^m=C_n^{n-m}$
• C_n^m=C_{n-1}^m+C_{n-1}^{m-1}
• $C_n^0+C_n^1+C_n^2+\dots+C_n^n=2^n$

---

4.8.1 求组合数 I

---

思想

• C_n^m=C_{n-1}^m+C_{n-1}^{m-1}
• 递推公式求组合数

模板例题 885. 求组合数 I

给定 n 组询问，每组询问给定两个整数 a，b，请你输出 Cbamod(109+7) 的值。

输入格式
第一行包含整数 n。

接下来 n 行，每行包含一组 a 和 b。

输出格式
共 n 行，每行输出一个询问的解。

数据范围
1≤n≤10000,
1≤b≤a≤2000
输入样例：

3
3 1
5 3
2 2

输出样例：

3
10
1

代码

#include <bits/stdc++.h>
using namespace std;

const int N=2010,mod=1e9+7;

int c[N][N];  //组合数

void init(){  //预处理出全部答案

    for(int i=0;i<N;i++){
        for(int j=0;j<=i;j++){
            if(!j) c[i][j]=1;  //如果j = 0，那么把c[i][j]初始化为1
            else c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;  //递推式
        }
    }

}

int main(){

    init();

    int n;

    cin>>n;

    while(n--){

        int a,b;

        cin>>a>>b;

        cout<<c[a][b]<<endl;

    }

    return 0;

}

---

4.8.2 求组合数 II

---

思想

• $C_{n}^{m}=\frac{n!}{m!(n-m)!}=n!\times(m!(n-m)!)^{-1}=n!\times m!^{-1}\times (n-m)!^{-1}$
• 预处理fact[N]和infact[N]，fact[i]存储$i!$，infact[i]存储$i!^{-1}$
• 则$C_n^m=$fact[n]*infact[m]*infact[n-m]
• 预处理时利用快速幂求逆元$\pmod {1e9+7}$

模板例题 886. 求组合数 II

原题链接

描述

给定 n 组询问，每组询问给定两个整数 a，b，请你输出 Cbamod(109+7) 的值。

输入格式
第一行包含整数 n。

接下来 n 行，每行包含一组 a 和 b。

输出格式
共 n 行，每行输出一个询问的解。

数据范围
1≤n≤10000,
1≤b≤a≤105
输入样例：

3
3 1
5 3
2 2

输出样例：

3
10
1

代码

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;

const int N=1e5+3,mod=1e9+7;

LL fact[N],infact[N];

LL qmi(LL a,LL k,LL p){

    int res=1;
    while(k){

        if(k&1) res=res*a%p;
        a=a*a%p;
        k>>=1;

    }

    return res;

}

int main(){

    fact[0]=infact[0]=1;

    for(int i=1;i<N;i++){

        fact[i]=fact[i-1]*i%mod;  //存储i!
        infact[i]=infact[i-1]*qmi(i,mod-2,mod)%mod;  //qmi(i,mod-2,mod)快速幂求逆元

    }

    LL n;

    cin>>n;

    while(n--){

        LL a,b;

        cin>>a>>b;

        cout<<fact[a]*infact[b]%mod*infact[a-b]%mod<<endl;  //计算公式

    }

    return 0;

}

---

4.8.3 求组合数 III

---

思想

• 卢卡斯定理：C_n^m\equiv C_{\frac{n}{p}}^{\frac{m}p}\times C_{n~mod~p}^{m~mod~p}\pmod p

• \begin{aligned} 证明:\\ &n=n_0p^0+n_1p^1+\dots+n_{k-1}p^{k-1}+n_kp^k\\ &m=m_0p^0+m_1p^1+\dots+m_{k-1}p^{k-1}+m_kp^k\\ \\ 则有：\\& \begin{aligned} (1+x)^n&=(1+x)^{n_0p^0+n_1p^1+\dots+n_{k-1}p^{k-1}+n_kp^k}\\ &=(1+x)^{n_0p^0}\times(1+x)^{n_1p^1}\times\dots\times(1+x)^{n_{k-1}p^{k-1}}\times(1+x)^{n_kp^k}\\ &=(1+x^{p^0})^{n_0}\times(1+x^{p^1})^{n_1}\times\dots\times(1+x^{p^{k-1}})^{n_{k-1}}\times(1+x^{p^k})^{n_k}\pmod p \end{aligned}\\ \\ &\because C_n^m在其等式左边即为x^m的系数，右边也为x^m的系数\\ 又&\because m的p进制:x^m=x^{m_0p^0+m_1p^1+\dots+m_{k-1}p^{k-1}+m_kp^k}\\ &\therefore x^{m_kp^k}项在(1+x^{p^k})^{n_k}中是C_{n_k}^{m_k}x^{m_kp^k},x^{m_{k-1}p^{k-1}}项在(1+x^{p^{k-1}})^{n_{k-1}}中是C_{n_{k-1}}^{m_{k-1}}x^{m_{k-1}p^{k-1}}\\ &同理:可得C_n^m=C_{n_0}^{m_0}\times C_{n_1}^{m_1}\times\dots\times C_{n_{k-1}}^{m_{k-1}}\times C_{n_k}^{m_k}\pmod p\\ \\ &\because n,m是p进制数\\ &\therefore n_0=n~mod~p,m_0=m~mod~p\\ &此时使得n,m在p进制下右移一位，即\lfloor \frac{n}{p}\rfloor,\lfloor \frac{m}{p}\rfloor\\ &对于\lfloor \frac{n}{p}\rfloor,\lfloor \frac{m}{p}\rfloor 重复上述步骤:\\ &C_{\lfloor \frac{n}{p}\rfloor}^{\lfloor \frac{m}{p}\rfloor}\equiv C_{n_1}^{m_1}\times C_{n_2}^{m_2}\times\dots\times C_{n_{k-1}}^{m_{k-1}}\times C_{n_k}^{m_k}\pmod p\\\\ &最终得到:C_n^m=C_{\lfloor \frac{n}{p}\rfloor}^{\lfloor \frac{m}{p}\rfloor}\times C_{n~mod~p}^{m~mod~p}\pmod p \end{aligned}

模板例题

原题链接

描述

给定 n 组询问，每组询问给定三个整数 a,b,p，其中 p 是质数，请你输出 Cbamodp 的值。

输入格式
第一行包含整数 n。

接下来 n 行，每行包含一组 a,b,p。

输出格式
共 n 行，每行输出一个询问的解。

数据范围
1≤n≤20,
1≤b≤a≤1018,
1≤p≤105,

输入样例：

3
5 3 7
3 1 5
6 4 13

输出样例：

3
3
2

代码

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;

LL qmi(LL a,LL k,LL p){

    LL res=1;

    while(k){

        if(k&1) res=res*a%p;
        a=a*a%p;
        k>>=1;

    }

    return res;

}

LL C(LL a,LL b,LL p){

    if(b>a) return 0;

    LL res=1;

    for(LL i=1,j=a;i<=b;i++,j--){

        res=res*j%p;
        res=res*qmi(i,p-2,p)%p;

    }

    return res;

}

LL lucas(LL a,LL b,LL p){

    if(a<p&&b<p) return C(a,b,p);
    return C(a%p,b%p,p)*lucas(a/p,b/p,p)%p;

}

int main(){

    int n;

    cin>>n;

    while(n--){

        LL a,b;

        LL p;

        cin>>a>>b>>p;

        cout<<lucas(a,b,p)<<endl;

    }

    return 0;

}

---

4.8.4 求组合数 IV

---

思想

• 利用高精度存储所有的方案数

模板例题 888. 求组合数 IV

原题链接

描述

输入 a,b，求 Cba 的值。

注意结果可能很大，需要使用高精度计算。

输入格式
共一行，包含两个整数 a 和 b。

输出格式
共一行，输出 Cba 的值。

数据范围
1≤b≤a≤5000

5 3

输出样例：

输出样例：

10

代码

#include <bits/stdc++.h>
using namespace std;

const int N=5010;

int primes[N];

int sum[N];

bool vis[N];

int cnt;

void get_primes(int n){

    for(int i=2;i<=n;i++){

        if(!vis[i]) primes[cnt++]=i;

        for(int j=0;primes[j]<=n/i;j++){

            vis[primes[j]*i]=1;
            if(i%primes[j]==0) break;

        }

    }

}

int get(int n,int p){

    int res=0;

    while(n){

        res+=n/p;
        n/=p;

    }

    return res;

}

vector<int> mul(vector<int> a,int b){

    vector<int> c;
    int t=0;

    for(int i=0;i<a.size();i++){

        t+=a[i]*b;
        c.push_back(t%10);
        t/=10;

    }

    while(t){
        c.push_back(t%10);
        t/=10;
    }

    return c;

}

int main(){

    int a,b;

    cin>>a>>b;

    get_primes(a);

    for(int i=0;i<cnt;i++){

        int p=primes[i];
        sum[i]=get(a,p)-get(a-b,p)-get(b,p);

    }

    vector<int> res;
    res.push_back(1);

    for(int i=0;i<cnt;i++){
        for(int j=0;j<sum[i];j++){
            res=mul(res,primes[i]);
        }
    }

    for(int i=res.size()-1;i>=0;i--) cout<<res[i];

    return 0;

}

---

4.9 容斥原理

---

思想

• 

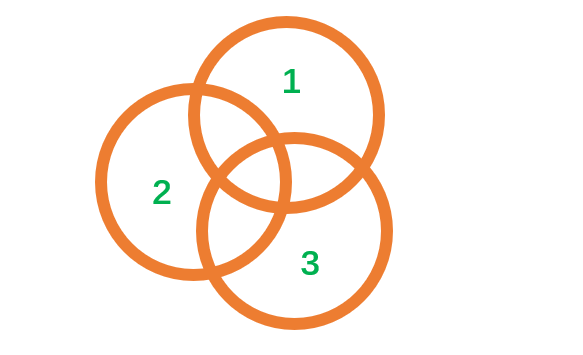
• 求S=S_1\cup S_2\cup S_3的面积：
  \begin{aligned} 由图可知:S=&S_1\cup S_2\cup S_3\\ =&S_1+S_2+S_3\\ &-S_1\cap S_2-S_1\cap S_3-S_2\cap S_3\\ &+S_1\cap S_2\cap S_3 \end{aligned}

• 推广求S=S_1\cup S_2\cup S_3\cap S_4的面积：
  \begin{aligned} S=&S_1\cup S_2\cup S_3\cap S_4\\ =&S_1+S_2+S_3+S_4\\ &-S_1\cap S_2-S_1\cap S_3-S_1\cap S_4-S_2\cap S_3-S_2\cap S_4-S_3\cap S_4\\ &+S_1\cap S_2\cap S_3+S_1\cap S_2\cap S_4+S_1\cap S_3\cap S_4+S_2\cap S_3\cap S_4\\ &-S_1\cap S_2\cap S_3\cap S_4 \end{aligned}

• 若将面积作为集合看待，则容易推出：
  \begin{aligned} &设U中元素有n种不同的属性，而第i种属性称为P_i拥有属性P_i的元素构成集合S_i,那么\\\\ &\begin{aligned} \Bigg|\bigcup_{i=1}^{n}S_i\Bigg|=&\sum_i|S_i|-\sum_{i\lt j}|S_i\cap S_j|+\sum_{i\lt j\lt k}|S_i\cap S_j\cap S_k|-\dots\\ &+(-1)^{m-1}\sum_{a_i\lt a_{i+1}}\Bigg|\bigcap_{i=1}^mS_{a_i}\Bigg|+\dots+(-1)^{n-1}|S_1\cap\dots\cap S_n|\\ \end{aligned}\\\\&即:\\\\&\Bigg|\bigcup_{i=1}^{n}S_i\Bigg|=\sum_{m=1}^n(-1)^{m-1}\sum_{a_i\lt a_{i+1}}\Bigg|\bigcap_{i=1}^mS_{a_i}\Bigg| \end{aligned}

模板例题 890. 能被整除的数

原题链接

给定一个整数 n 和 m 个不同的质数 p1,p2,…,pm。

请你求出 1∼n 中能被 p1,p2,…,pm 中的至少一个数整除的整数有多少个。

输入格式
第一行包含整数 n 和 m。

第二行包含 m 个质数。

输出格式
输出一个整数，表示满足条件的整数的个数。

数据范围
1≤m≤16,
1≤n,pi≤109
输入样例：

10 2
2 3

输出样例：

7

代码

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;

const int N=20;

int p[N];

int main(){

    int n,m;

    cin>>n>>m;

    for(int i=0;i<m;i++) cin>>p[i];

    LL res=0;

    for(int i=1;i<1<<m;i++){  // 1~2^m-1这些数代表2^m-1个不同的项

        LL t=1,s=0;  //s代表当前枚举的项中包含集合的个数 

        for(int j=0;j<m;j++){  //看这个项的第 j 位是否包含，1代表包含，0代表不包含 

            if(i>>j&1){  //选 

                if(t*p[j]>n){   //此时 n/t = 0，直接break即可 
                    t=-1;
                    break;
                }

                t*=p[j];
                s++;

            }

        }

        if(t!=-1){

            if(s%2) res+=n/t;  //加奇数项的个数 
            else res-=n/t;  //减偶数项的个数 

        }

    }

    cout<<res<<endl;

    return 0;

}

---

4.10 博弈论

---

概念

若一个游戏满足：

• 由两名玩家交替行动
• 在游戏进行的任意时刻，可以执行的合法行动与轮到哪位玩家无关
• 不能行动的玩家判负

则称该游戏为一个公平组合游戏

尼姆游戏（NIM）属于公平组合游戏，但常见的棋类游戏，比如围棋就不是公平组合游戏，因为围棋交战双方分别只能落黑子和白子，胜负判定也比较负责，不满足条件2和3

---

4.10.1 Nim 游戏

---

游戏规则

给定n堆石子，两位玩家轮流操作，每次操作可以从任意一堆石子中拿走任意数量的石子（可以拿完，但不能不拿），最后无法进行操作的人视为失败。
问如果两人都采用最优策略，先手是否必胜。

例如：有两堆石子，第一堆有2个，第二堆有3个，先手必胜。

操作步骤

• 先手从第二堆拿走1个，此时第一堆和第二堆数目相同
• 无论后手怎么拿，先手都在另外一堆石子中取走相同数量的石子即可

思想

• 必胜状态：先手进行某一个操作，留给后手是一个必败状态时，对于先手来说是一个必胜状态。即先手可以走到某一个必败状态
• 必败状态：先手无论如何操作，留给后手都是一个必胜状态时，对于先手来说是一个必败状态。即先手走不到任何一个必败状态
• 结论：假设有n堆石子，数目分别是a_1,a_2,\dots,a_n，如果a_1\oplus a_2\oplus\dots\oplus a_n\ne 0，先手必胜；否则先手必败。

证明

• 操作到最后时，每堆石子数都是0，即：$0\oplus 0\oplus\dots\oplus0=0$

• 在操作过程中，如果$a_1\oplus a_2\oplus\dots\oplus a_n=x\ne 0$，那么玩家必然可以通过拿走某一堆若干个石子将异或结果变为$0$
  \begin{aligned} 证明：&\\ &设x的二进制表示中最高一位1在第k位\\ &则a_1,a_2,\dots,a_n中，必然有一个数a_i，它的第k为1\\ &且一定满足:a_i\oplus x\lt a_i\\ &若从第i堆石子中拿走(a_i−a_i\oplus x)个石子\\ &则第i石子还剩a_i−(a_i−a_i\oplus x)==a_i\oplus x个石子\\ &由：a_1\oplus a_2\oplus\dots\oplus a_i \oplus\dots a_n=x\ne 0可知\\ &此时：a_1\oplus a_2\oplus\dots\oplus a_i\oplus x \oplus\dots a_n=x\oplus x=0 \end{aligned}

• 在操作过程中，如果$a_1\oplus a_2\oplus\dots\oplus a_n=x=0$，那么无论玩家怎么拿，必然会导致最终异或结果不为$0$
  \begin{aligned} 反证明：&\\ &假设玩家从第i堆石子拿走若干个，结果仍是0\\ &不妨设拿走后，第i堆还剩下a'个石子，且a'\lt a_i\\ &此时仍有：a_1\oplus a_2\oplus\dots\oplus a'\oplus\dots a_n=0\\ &则有(a_1\oplus a_2\oplus\dots\oplus a'\oplus\dots a_n)=(a_1\oplus a_2\oplus\dots\oplus a_i\oplus\dots a_n)=a'\oplus a_i=0\\ &即：a'=a_i，与原假设a'\lt a_i矛盾\\ &故假设不成立 \end{aligned}

• 综上：若先手面对的局面是$a_1\oplus a_2\oplus\dots\oplus a_n\ne 0$，则先手必胜，反之先手必败

---

模板例题 891. Nim游戏

原题链接

描述

给定 n 堆石子，两位玩家轮流操作，每次操作可以从任意一堆石子中拿走任意数量的石子（可以拿完，但不能不拿），最后无法进行操作的人视为失败。

问如果两人都采用最优策略，先手是否必胜。

输入格式
第一行包含整数 n。

第二行包含 n 个数字，其中第 i 个数字表示第 i 堆石子的数量。

输出格式
如果先手方必胜，则输出 Yes。

否则，输出 No。

数据范围
1≤n≤105,
1≤每堆石子数≤109
输入样例：

2
2 3

输出样例：

Yes

代码

#include <bits/stdc++.h>
using namespace std;

int main(){

    int n;

    cin>>n;

    int res;

    cin>>res;

    for(int i=0;i<n-1;i++){

        int m;

        cin>>m;

        res^=m;

    }

    if(res) cout<<"Yes"<<endl;
    else cout<<"No"<<endl;

    return 0;

}

---

4.10.2 台阶-Nim 游戏

---

原题链接

描述

现在，有一个 n 级台阶的楼梯，每级台阶上都有若干个石子，其中第 i 级台阶上有 ai 个石子(i≥1)。

两位玩家轮流操作，每次操作可以从任意一级台阶上拿若干个石子放到下一级台阶中（不能不拿）。

已经拿到地面上的石子不能再拿，最后无法进行操作的人视为失败。

问如果两人都采用最优策略，先手是否必胜。

输入格式
第一行包含整数 n。

第二行包含 n 个整数，其中第 i 个整数表示第 i 级台阶上的石子数 ai。

输出格式
如果先手方必胜，则输出 Yes。

否则，输出 No。

数据范围
1≤n≤105,
1≤ai≤109
输入样例：

3
2 1 3

输出样例：

Yes

分析

• 在采取最优策略的情况下，一方玩家对于偶数级台阶的操作的影响，可以被另一方玩家做相同操作的结果消去
• 故只考虑奇数级台阶的情况，适用于经典Nim游戏
• 即：对于奇数级台阶，若先手面对的局面是$a_1\oplus a_3\oplus\dots\oplus a_n\ne 0$，则先手必胜，反之先手必败

代码

#include <bits/stdc++.h>
using namespace std;

int main(){

    int n;

    cin>>n;

    int res;

    cin>>res;

    for(int i=2;i<=n;i++){
        int m;
        cin>>m;
        if(i%2) res^=m;
    }

    if(res) cout<<"Yes"<<endl;
    else cout<<"No"<<endl;

    return 0;

}

---

4.10.3 集合-Nim 游戏

---

游戏规则

给定n堆石子以及一个由k个不同正整数构成的数字集合S。

现在有两位玩家轮流操作，每次操作可以从任意一堆石子中拿取石子，每次拿取的石子数量必须包含于集合S，最后无法进行操作的人视为失败。

问如果两人都采用最优策略，先手是否必胜。

核心思想

• Mex运算：设$S$表示一个非负整数集合，定义$Mex(S)$为求出不属于集合$S$的最小自然数运算，例如：$S=\lbrace 0,1,2,4\rbrace$，则$Mes(S)=3$
• $SG$函数：在有向图游戏中，对于每个节点$x$,设从$x$出发共有$k$条有向边，分别到达节点$y_1,y_2\dots y_k$，定义$SG(x)$的后记节点$y_1,y_2\dots y_k$的$SG$函数值构成的集合在执行$Mex$运算的结果，即：$SG(x)=Mex(\lbrace SG(y_1),SG(y_2)\dots SG(y_k)\rbrace)$，特别地，整个有向图游戏$G$的$SG$函数值被定义为有向图游戏起点$s$的$SG$函数值，即 $SG(G)=SG(s)$
• $SG$函数的性质：
  • 定义终点的$SG$函数值为$0$，
  • $SG(i)=k,k\ne 0$，则$i$最大能到达的点的$SG$的范围为$[0,k−1)$
  • 若$SG(i)=0$，说明走不到$0$
• 有向图游戏的和：若一个游戏的每个局面都可以构成一个有向图，则对于每个有向图的$SG(G_1),SG(G_2)\dots SG(G_n)$，对所有图的$SG$进行异或运算，即可得到该有向图游戏的和，且其结果满足Nim游戏

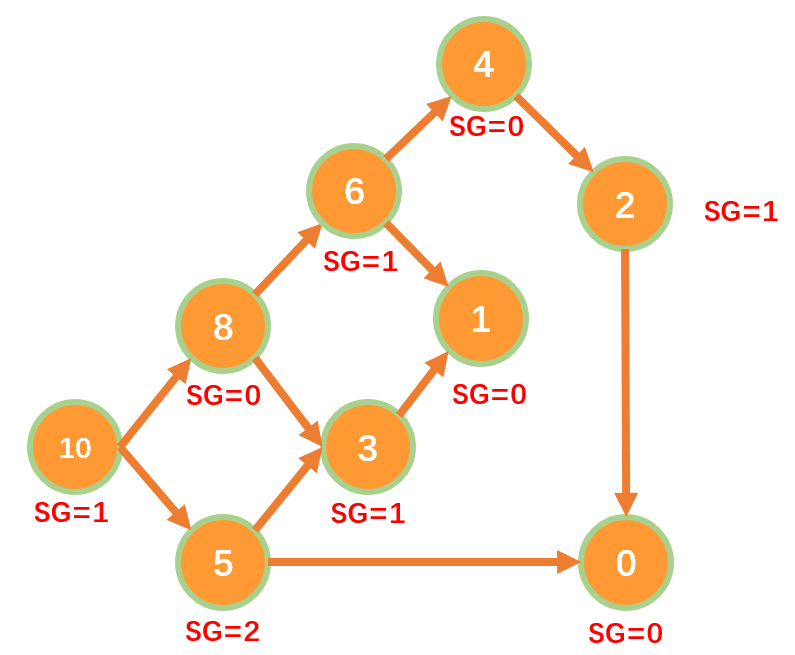
$SG$函数图解

• 根据每一步的不同选择生成路径单一的有向图，每条不同的路径对应不同的局面（方案）
• 定义终点的$SG$函数值为$0$，倒推起点的$SG$函数值
• 设一堆石子有$10$个，每次操作可取的数量为$S=\lbrace 2,5\rbrace$，无法操作即为终点，其$SG$函数如下：
• 

证明有向图游戏的和符合Nim游戏

• 操作到最后时，每一种局面的$SG(G_i)$值都是$0$，即：$0\oplus 0\oplus\dots\oplus0=0$

• 在操作过程中，如果$SG(G_1)\oplus SG(G_2)\oplus\dots\oplus SG(G_n)=x\ne 0$，由$SG$函数的性质可知，玩家必然可以走到某一局面将异或结果变为$0$
  \begin{aligned} 证明：&\\ &设x的二进制表示中最高一位1在第k位\\ &则SG(G_1),SG(G_2),\dots,SG(G_n)中，必然有一个局面SG(G_i)，其值的第k为1\\ &且一定满足:SG(G_i)\oplus x\lt SG(G_i)\\ &若将第i个局面的SG值取到(SG(G_i)\oplus x)\\ &由：SG(G_1)\oplus SG(G_2)\oplus\dots\oplus SG(G_i) \oplus\dots SG(G_n)=x\ne 0可知\\ &此时：SG(G_1)\oplus SG(G_2)\oplus\dots\oplus SG(G_i)\oplus x \oplus\dots SG(G_n)=x\oplus x=0 \end{aligned}

• 在操作过程中，如果$SG(G_1)\oplus SG(G_2)\oplus\dots\oplus SG(G_n)=x=0$，那么无论玩家如何更改局面，必然会导致最终异或结果不为$0$
  \begin{aligned} 反证明：&\\ &假设玩家改变第i个局面的SG值，结果仍是0\\ &不妨设SG(G_i)改变后的值为SG(G_i)'，且SG(G_i)'\lt SG(G_i)\\ &此时仍有：SG(G_1)\oplus SG(G_2)\oplus\dots\oplus SG(G_i)'\oplus\dots SG(G_n)=0\\ &则有(SG(G_1)\oplus SG(G_2)\oplus\dots\oplus SG(G_i)'\oplus\dots SG(G_n))\\&=(SG(G_1)\oplus SG(G_2)\oplus\dots\oplus SG(G_i)\oplus\dots SG(G_n))=SG(G_i)'\oplus SG(G_i)=0\\ &即：SG(G_i)'=SG(G_i)，与原假设SG(G_i)'\lt SG(G_i)矛盾\\ &故假设不成立 \end{aligned}

• 综上：若先手面对的局面是$SG(G_1)\oplus SG(G_2)\oplus\dots\oplus SG(G_n)=x\ne 0$，则先手必胜，反之先手必败，符合Nim游戏

模板例题 893. 集合-Nim游戏

原题链接

描述

给定 n 堆石子以及一个由 k 个不同正整数构成的数字集合 S。

现在有两位玩家轮流操作，每次操作可以从任意一堆石子中拿取石子，每次拿取的石子数量必须包含于集合 S，最后无法进行操作的人视为失败。

问如果两人都采用最优策略，先手是否必胜。

输入格式
第一行包含整数 k，表示数字集合 S 中数字的个数。

第二行包含 k 个整数，其中第 i 个整数表示数字集合 S 中的第 i 个数 si。

第三行包含整数 n。

第四行包含 n 个整数，其中第 i 个整数表示第 i 堆石子的数量 hi。

输出格式
如果先手方必胜，则输出 Yes。

否则，输出 No。

数据范围
1≤n,k≤100,
1≤si,hi≤10000
输入样例：

2
2 5
3
2 4 7

输出样例：

Yes

代码

#include <bits/stdc++.h>
using namespace std;

const int N=1e6+3;

int n,m;

int s[N],f[N];  //s存储的是可供选择的集合,f存储的是所有可能出现过的情况的sg值

int sg(int x){

    if(f[x]!=-1) return f[x];  //如果存储过了,直接返回

    set<int> vis;   //vis代表的是当前存在的数的集合

    for(int i=0;i<m;i++){

        int sum=s[i];
        if(x>=sum) vis.insert(sg(x-sum));  //先得到到终点的sg值后,再从后往前倒推出所有数的sg值

    }

    for(int i=0;;i++){
        if(!vis.count(i)) return f[x]=i;  //Mex操作

}

int main(){

    cin>>m;

    for(int i=0;i<m;i++) cin>>s[i];

    cin>>n;

    memset(f,-1,sizeof f); 

    int res=0;

    for(int i=0;i<n;i++){

        int x;

        cin>>x;

        res^=sg(x);  //Nim游戏

    }

    if(res) cout<<"Yes"<<endl;
    else cout<<"No"<<endl;

    return 0;

}

---

4.10.4 拆分-Nim 游戏

---

原题链接

描述

给定 n 堆石子，两位玩家轮流操作，每次操作可以取走其中的一堆石子，然后放入两堆规模更小的石子（新堆规模可以为 0，且两个新堆的石子总数可以大于取走的那堆石子数），最后无法进行操作的人视为失败。

问如果两人都采用最优策略，先手是否必胜。

输入格式
第一行包含整数 n。

第二行包含 n 个整数，其中第 i 个整数表示第 i 堆石子的数量 ai。

输出格式
如果先手方必胜，则输出 Yes。

否则，输出 No。

数据范围
1≤n,ai≤100

输出样例：

2
2 3

输出样例：

Yes

分析

• 相比于集合-Nim，这里的每一堆可以变成小于原来那堆的任意大小的两堆，即a[i]可以拆分成(b[i],b[j])
• 为了避免重复，规定b[i]>=b[j],即：a[i]>b[i]>=b[j]
• 相当于一个局面拆分成了两个局面，由$SG$函数理论，多个独立局面的$SG$值，等于这些局面$SG$值的异或和。因
• 此需要存储的状态就是sg(b[i])^sg(b[j])

代码

#include <bits/stdc++.h>
using namespace std;

const int N=1e6+3;

int n;

int f[N];

set<int> vis;

int sg(int x){

    if(f[x]!=-1) return f[x];

    for(int i=0;i<x;i++){
        for(int j=0;j<=i;j++){  //规定j不大于i，避免重复
            vis.insert(sg(i)^sg(j));  //相当于一个局面拆分成了两个局面
        }
    }

    for(int i=0;;i++){
        if(!vis.count(i)) return f[x]=i;
    }

}

int main(){

    cin>>n;

    memset(f,-1,sizeof f);

    int res=0;

    for(int i=0;i<n;i++){

        int x;

        cin>>x;

        res^=sg(x);

    }

    if(res) cout<<"Yes"<<endl;
    else cout<<"No"<<endl;

    return 0;

}