本文最后更新于 587 天前,其中的信息可能已经有所发展或是发生改变。
1. 邻接矩阵
思想:
- 利用二维数组
g[N][N]存储所有的点到点的权值。 - 其中
N为点的数量,g[i][j]表示点i到点j的权值。
时间复杂度:$\mathcal{O}(n^2)$
空间复杂度:$\mathcal{O}(n^2)$
应用:
- 只在点数不多的稠密图使用。
- 大部分情况下点的数量 $n = 10^3$,边的数量 $m = 10^6$。
示例:
- 现有
n个点共m条边,以及每条边的起始点和终点及权值。 - 这些点和边共同构成一个有向图。
- 存储这些信息并输出。
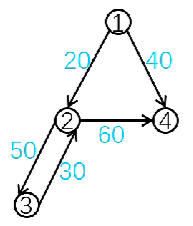
输入:
4 5
1 2 20
1 4 40
2 3 50
2 4 60
3 2 30代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 1010; //图的大小
int n, m;
int g[N][N];
bool vis[N]; //标记是否走过
void dfs(int u){ //深度优先遍历
vis[u] = 1; //标记当前点已经遍历过
for(int i = 1; i <= n; i ++){ //遍历n个点
if(g[u][i] != 0){
cout << u << ' ' << i << ' ' << g[u][i] << endl;
if(vis[i]) continue; //当前的边的终点已经走过则跳过
dfs(i);
}
}
}
void solve(){
cin >> n >> m;
for(int i = 0; i < m; i ++){
int a, b, c; cin >> a >> b >> c;
g[a][b] = c;
// g[b][a] = c; //如果是无向图加一条边
}
dfs(1); //从1号点开始遍历
}
int main(){
solve();
return 0;
}输出:
1 2 20
2 3 50
3 2 30
2 4 60
1 4 402. 边集数组
思想:
- 利用结构体数组
e[N]存储边的信息。 - 其中
e[i]包含第i条边的{起始点u, 终点v, 边权w}。
时间复杂度:$\mathcal{O}(nm)$
空间复杂度:$\mathcal{O}(m)$
应用:
- 在
Kruskal算法中,需要将边按照边权排序,直接存边。
示例:
- 现有
n个点共m条边,以及每条边的起始点和终点及权值。 - 这些点和边共同构成一个有向图。
- 存储这些信息并输出。
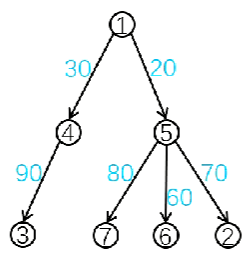
输入:
7 6
4 3 90
1 4 30
5 7 80
5 6 60
1 5 20
5 2 70代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 1010; //图的大小
int n, m;
struct edge{
int u, v, w;
}e[N];
bool vis[N]; //标记是否走过
void dfs(int u){ //深度优先遍历
vis[u] = 1; //标记当前点已经遍历过
for(int i = 1; i <= m; i ++){ //遍历m条边
if(u == e[i].u){ //找到当前的边的起始点
cout << e[i].u << ' ' << e[i].v << ' ' << e[i].w << endl;
if(vis[e[i].v]) continue; //当前的边的终点已经走过则跳过
dfs(e[i].v);
}
}
}
void solve(){
cin >> n >> m;
for(int i = 1; i <= m; i ++){
int a, b, c; cin >> a >> b >> c;
e[i] = {a, b, c};
// e[i] = {b, a, c}; //如果是无向图加一条边
}
dfs(1); //从1号点开始遍历
}
int main(){
solve();
return 0;
}输出:
1 4 30
4 3 90
1 5 20
5 7 80
5 6 60
5 2 70 3. 邻接表
思想:
- 利用出边数组
e[N][N]存储边的信息。 - 其中
e[u][i]表示点u的所有出边,其出边包含{终点v, 边权w}。
时间复杂度:$\mathcal{O}(n+m)$
空间复杂度:$\mathcal{O}(n+m)$
应用:
- 可以应用于各种图,但是不能处理反向的边(网络流)。
示例:
- 现有
n个点共m条边,以及每条边的起始点和终点及权值。 - 这些点和边共同构成一个有向图。
- 存储这些信息并输出。

输入:
7 6
4 3 90
1 4 30
5 7 80
5 6 60
1 5 20
5 2 70代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 1010; //图的大小
int n, m;
struct edge{
int v, w;
};
vector<edge> e[N]; //边集
void dfs(int u, int fa){ //深度优先遍历, fa记录当前点的父节点
for(auto p : e[u]){ //遍历所有的出边
if(fa == p.v) continue; //若该出边的终点是父节点,说明已经走过
cout << u << ' ' << p.v << ' ' << p.w << endl;
dfs(p.v, u);
}
}
void solve(){
cin >> n >> m;
for(int i = 1; i <= m; i ++){
int a, b, c; cin >> a >> b >> c;
e[a].push_back({b, c});
// e[b].push_back({a, c}); //如果是无向图加一条边
}
dfs(1, 0); //从1号点开始遍历
}
int main(){
solve();
return 0;
}输出:
1 4 30
4 3 90
1 5 20
5 7 80
5 6 60
5 2 70 4. 链式邻接表
思想:
- 利用边集数组
e[N]存储所有的边的信息,表头数组h[N][N]存储点的所有出边的编号。 - 其中
e[j]存储第j条边的{起始u, 终点v, 边权w},h[u][i]存储u点的第i条边的编号。
时间复杂度:$\mathcal{O}(n+m)$
空间复杂度:$\mathcal{O}(n+m)$
应用:
- 可以应用于各种图,也能处理反向的边。
示例:
- 现有
n个点共m条边,以及每条边的起始点和终点及权值。 - 这些点和边共同构成一个无向图。
- 存储这些信息并输出。
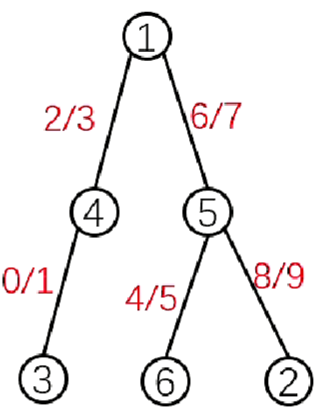
输入:
6 5
4 3 90
1 4 30
5 6 60
1 5 20
5 2 70代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 1010; //图的大小
int n, m;
struct edge{
int u, v, w;
};
vector<edge> e; //边集
vector<int> h[N]; //点的所有出边
void add(int a, int b, int c){
e.push_back({a, b, c});
h[a].push_back(e.size() - 1);
}
void dfs(int u, int fa){ //深度优先遍历, fa记录当前点的父节点
for(int i = 0; i < h[u].size(); i ++){
int j = h[u][i];
if(fa == e[j].v) continue;
cout << u << ' ' << e[j].v << ' ' << e[j].w << endl;
dfs(e[j].v, u);
}
}
void solve(){
cin >> n >> m;
for(int i = 1; i <= m; i ++){
int a, b, c; cin >> a >> b >> c;
add(a, b, c);
add(b, a, c); //如果是无向图加一条边
}
dfs(1, 0); //从1号点开始遍历
}
int main(){
solve();
return 0;
}输出:
1 4 30
4 3 90
1 5 20
5 6 60
5 2 705. 链式前向星
思想:
- 一个表头悬挂多个链表。
- 利用边集数组
e[N]存储所有的出边的信息,表头数组h[N]存储点的第一条出边的编号。 - 其中
e[i]存储第i条边的{终点v, 边权w, 下一条边ne},h[u]存储u点的第一条出边的编号。
时间复杂度:$\mathcal{O}(n+m)$
空间复杂度:$\mathcal{O}(n+m)$
应用:
- 可以应用于各种图,也能处理反向的边。
示例:
- 现有
n个点共m条边,以及每条边的起始点和终点及权值。 - 这些点和边共同构成一个无向图。
- 存储这些信息并输出。

输入:
6 5
4 3 90
1 4 30
5 6 60
1 5 20
5 2 70代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 3; //图的大小
int n, m;
struct edge{
int v, w, ne;
}e[N]; //边集
int idx, h[N]; //点的第一条出边,idx为下标编号
void add(int a, int b, int c){
e[idx] = {b, c, h[a]};
h[a] = idx ++;
}
void dfs(int u, int fa){ //深度优先遍历, fa记录当前点的父节点
for(int i = h[u]; ~ i; i = e[i].ne){
if(fa == e[i].v) continue;
cout << u << ' ' << e[i].v << ' ' << e[i].w << endl;
dfs(e[i].v, u);
}
}
void solve(){
cin >> n >> m;
memset(h, -1, sizeof h); //初始化第一条出边为-1
for(int i = 1; i <= m; i ++){
int a, b, c; cin >> a >> b >> c;
add(a, b, c);
add(b, a, c); //如果是无向图加一条边
}
dfs(1, 0); //从1号点开始遍历
}
int main(){
solve();
return 0;
}输出:
1 5 20
5 2 70
5 6 60
1 4 30
4 3 90总结
- 链式邻接表和链式前向星可以解决绝大部分的图论问题。
- 推荐使用链式前向星,建图方式简便,空间压缩紧密,查找效率高。