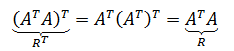1. 基本概念

---

1.1 行列式

---

二阶行列式：

$\left|\begin{matrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{matrix}\right| = a_{11}\times a_{12} - a_{21}\times a_{22}$

• 对于 $a_{ij}$：$i$ 表示行标，$j$ 表示列标。
• 对角线 $a_{11}a_{22}$ 为主对角线；$a_{12}a_{21}$ 为次对角线

三阶行列式：

$\left|\begin{matrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33} \end{matrix}\right| = \begin{aligned}&a_{11}\times a_{22}\times a_{33} + a_{21}\times a_{32}\times a_{33} + a_{12}\times a_{23}\times a_{31}\\&-a_{13}\times a_{22}\times a_{31} - a_{23}\times a_{32}\times a_{11} - a_{12}\times a_{21}\times a_{33}\end{aligned}$

---

1.2 线性方程组

---

$n$ 元非齐次线性方程组：

• 设有 $n$ 个未知数 $m$ 个方程的线性方程组，其中 $a_{ij}$ 是第 $i$ 个方程第 $j$ 个未知数的系数，$b_i$ 是第 $i$ 个方程的常数项，且 $b_i$ 不全为 $0$。

$\begin{cases} a_{11}x_1+a_{12}x_2+\dots+a_{1n}x_n=b_1\\\\ a_{21}x_1+a_{22}x_2+\dots+a_{2n}x_n=b_2\\\\ \dots\\\\ a_{n1}x_1+a_{n2}x_2+\dots+a_{nn}x_n=b_n\\ \end{cases}\\$

$n$ 元齐次线性方程组：

• 设有 $n$ 个未知数 $m$ 个方程的线性方程组，其中 $a_{ij}$ 是第 $i$ 个方程第 $j$ 个未知数的系数，$b_i$ 是第 $i$ 个方程的常数项，且 $b_i = 0$。

$\begin{cases} a_{11}x_1+a_{12}x_2+\dots+a_{1n}x_n=0\\\\ a_{21}x_1+a_{22}x_2+\dots+a_{2n}x_n=0\\\\ \dots\\\\ a_{n1}x_1+a_{n2}x_2+\dots+a_{nn}x_n=0\\ \end{cases}\\$

线性方程组：

• $n$ 元线性方程组简称线性方程组或方程组。

---

1.3 矩阵

---

1.3.1 矩阵的定义

---

二阶矩阵：

$\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}$

三阶矩阵：

$\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33} \end{bmatrix}$

$m\times n$ 矩阵：

• 由 $m\times n$ 个数 $a_{ij}(i = 1, 2, \dots, m, j = 1, 2, \dots,n)$ 排列成的 $m$ 行 $n$ 列的数表。

$A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1 n} \\ a_{21} & a_{22} & \cdots & a_{2 n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m 1} & a_{m 2} & \cdots & a_{m n} \end{bmatrix}$

与线性方程组相关的矩阵：

对于非齐次线性方程组：
$\begin{cases} a_{11}x_1+a_{12}x_2+\dots+a_{1n}x_n=b_1\\\\ a_{21}x_1+a_{22}x_2+\dots+a_{2n}x_n=b_2\\\\ \dots\\\\ a_{n1}x_1+a_{n2}x_2+\dots+a_{nn}x_n=b_n\\ \end{cases}\\$
有如下矩阵：
$A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1 n} \\ a_{21} & a_{22} & \cdots & a_{2 n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m 1} & a_{m 2} & \cdots & a_{m n} \end{bmatrix}, X = \begin{bmatrix}x_1\\x_2\\\vdots\\x_n\end{bmatrix}, b = \begin{bmatrix}b_1\\b_2\\\vdots\\b_n\end{bmatrix}, B = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1 n} &b_{1}\\ a_{21} & a_{22} & \cdots & a_{2 n} &b_{2}\\ \vdots & \vdots & \ddots & \vdots &\vdots\\ a_{m 1} & a_{m 2} & \cdots & a_{m n}&b_{m}\\ \end{bmatrix}$
其中：

• $A$ 为系数矩阵。
• $X$ 为未知数矩阵。
• $b$ 为常数项矩阵。
• $B$ 为增广矩阵。

---

1.3.2 矩阵的计算

---

加减：

• 两个矩阵相加或相减，需要满足两个矩阵的列数和行数一致。

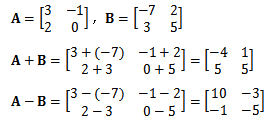
• 满足交换律： $A + B = B + A$

乘法：

• 两个矩阵 $A$ 和 $B$ 相乘，需要满足 $A$ 的列数等于 $B$ 的行数。

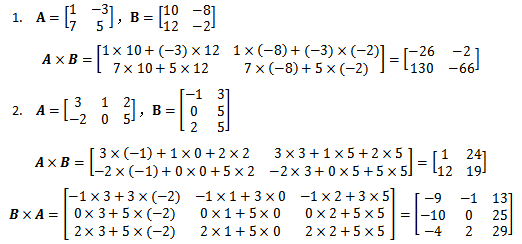
• 矩阵乘法不满足交换律：$AB\ne BA$，但仍然满足结合律和分配律：

---

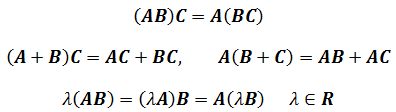
1.3.3 零矩阵和单位矩阵

---

零矩阵：

• 元素都是 $0$ 的矩阵称为零矩阵，记作 $O$。
• 不同型的零矩阵是不同的。

单位矩阵：

• 单位矩阵是一个 $n\times n$ 矩阵，从左到右的对角线（主对角线）上的元素是 $1$，其余元素都为 $0$。

下面是三个单位矩阵：

• 若矩阵 $A$ 为 $n\times n$ 的方阵，$E$ 为单位矩阵，则：$AE=A,EA=A$

---

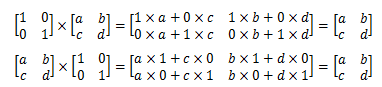
1.3.4 逆矩阵和奇异矩阵

---

逆矩阵：

• 矩阵 $A$ 的逆矩阵记作 $A^{-1}$。
• $AA^{-1} = E$，其中 $E$ 为单位矩阵。

奇异矩阵：

• 当一个矩阵没有逆矩阵的时候，称该矩阵为奇异矩阵。
• 当且仅当一个矩阵的行列式为零时，该矩阵是奇异矩阵。

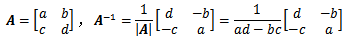
当 $a\times d-b\times c=0$ 时 $A$ 没有定义，$A^{-1}$不存在，则 $A$ 是奇异矩阵。

如 ：$A=\begin{bmatrix}1&1\\2&2\end{bmatrix}$ 是奇异矩阵。

---

1.3.5 矩阵转置

---

• 将矩阵 $A$ 的行换成同序数的列得到的新的矩阵，叫做 $A$ 的转置矩阵，记作： $A^T$。

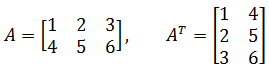
• 转置运算公式：

---

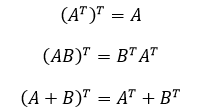
1.3.6 对称矩阵

• 如果一个矩阵转置后等于原矩阵，那么这个矩阵称为对称矩阵。

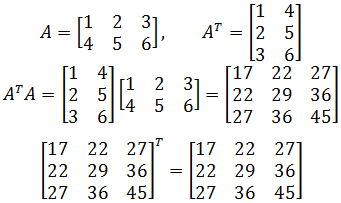
• 由定义可知，对称矩阵一定是方阵。

• 对称矩阵很常见，实际上，一个矩阵转置和这个矩阵的乘积就是一个对称矩阵：

  

• 两个对称矩阵相加，仍然得到对称矩阵：

---

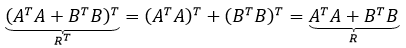
2. 方程组的解释

---

2.1 二元方程组及其矩阵

---

设方程组有 $2$ 个未知数，一共有 $2$ 个方程：

• 则有方程组 $\begin{cases}2x&-y&=0\\-x&+2y&=3\end{cases}$
• 写作矩阵形式有 $\begin{bmatrix}2&-1\\-1&2\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}0\\3\end{bmatrix}$

通常我们把第一个矩阵称为系数矩阵 $A$，将第二个矩阵称为向量 $x$，将第三个矩阵称为向量 $b$，于是线性方程组可以表示为 $Ax=b$。

---

行图像：

• 即直角坐标系中的图像。

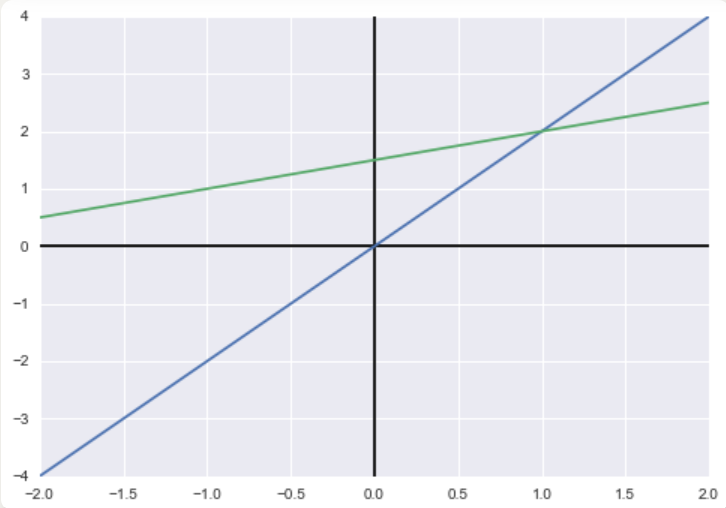
解释：

• 上图是直角坐标系中方程组中的两直线相交的情况。
• 接下来我们按列观察方程组：
  • $x\begin{bmatrix}2\\-1\end{bmatrix}+y\begin{bmatrix}-1\\2\end{bmatrix}=\begin{bmatrix}0\\3\end{bmatrix}$
• 我们把第一个向量称作 $col_1$，第二个向量称作 $col_2$，分别表示第一列的向量和第二列的向量。
• 要使得式子成立需要第一个向量加上两倍的第二个向量，即：
  • $1\times col_1 + 2\times col_2 = 1\begin{bmatrix}2\\-1\end{bmatrix}+2\begin{bmatrix}-1\\2\end{bmatrix}=\begin{bmatrix}0\\3\end{bmatrix}$
• 这和我们方程组的解 $x = 1,y = 2$ 是对应的。

---

列图像：

• 即在二维平面上画出上面的列向量。

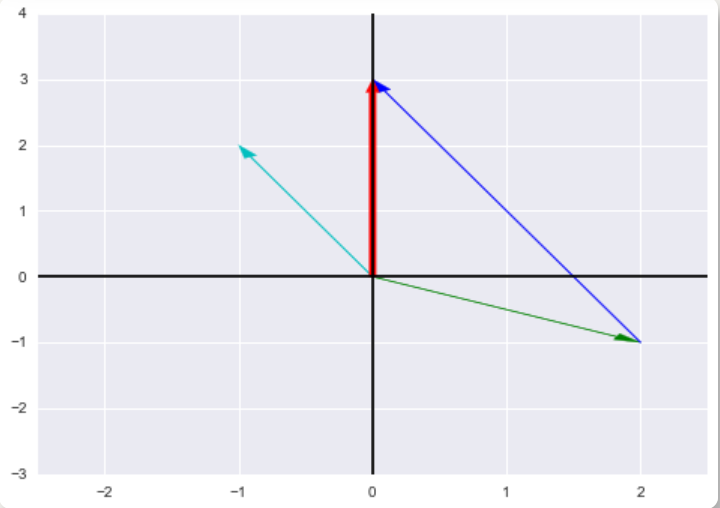
解释：

• 绿向量 $col_1$与蓝向量（两倍的绿向量 $col_2$）合成红向量 $b$。
• 接下来我们继续观察方程组：
  • $x\begin{bmatrix}2\\-1\end{bmatrix}+y\begin{bmatrix}-1\\2\end{bmatrix}=\begin{bmatrix}0\\3\end{bmatrix}$
• 显然地，$col_1$ 和 $col_2$ 通过某种线性组合得到了向量 $b$，即：
  • $1\times col_1 + 2\times col_2 = 1\begin{bmatrix}2\\-1\end{bmatrix}+2\begin{bmatrix}-1\\2\end{bmatrix}=\begin{bmatrix}0\\3\end{bmatrix}$
• 那么推广来看， $col_1$ 和 $col_2$ 通过所有的线性组合所得到的向量 $b_i$ 将能够铺满整个平面。

---

2.2 三元方程组及其矩阵

---

设方程组有 $3$ 个未知数，一共有 $3$ 个方程：

• 则有方程组 $\begin{cases}2x&-y&&=0\\-x&+2y&-z&=-1\\&-3y&+4z&=4\end{cases}$
• 写作矩阵形式有 $A=\begin{bmatrix}2&-1&0\\-1&2&-1\\0&-3&4\end{bmatrix},\\ b=\begin{bmatrix}0\\-1\\4\end{bmatrix}$

---

行图像的解释：

• 在三维直角坐标系中，每一个方程将确定一个平面。
• 接下来我们按列观察方程组：
  • $x\begin{bmatrix}2\\-1\\0\end{bmatrix}+y\begin{bmatrix}-1\\2\\-3\end{bmatrix}+z\begin{bmatrix}0\\-1\\4\end{bmatrix}=\begin{bmatrix}0\\-1\\4\end{bmatrix}$
• 该例子中的三个平面会相交于一点 $(0,0,1)$，这个点就是方程组的解，且带入 $x = 0,y = 0,z = 1$ 也可以使得上述式子成立。

---

列图像的解释：

• 观察列图像的向量 $col_1,col_2,col3$ 的组合。
• 继续观察方程组：
  • $x\begin{bmatrix}2\\-1\\0\end{bmatrix}+y\begin{bmatrix}-1\\2\\-3\end{bmatrix}+z\begin{bmatrix}0\\-1\\4\end{bmatrix}=\begin{bmatrix}0\\-1\\4\end{bmatrix}$
• 显然地，$col_1,col_2,col_3$ 也可以通过某种线性组合得到向量 $b$，即：
  • $0\times col_1 + 0\times col_2 + 1\times col_3= 0\begin{bmatrix}2\\-1\\0\end{bmatrix}+0\begin{bmatrix}-1\\2\\-3\end{bmatrix}+1\begin{bmatrix}0\\-1\\4\end{bmatrix}=\begin{bmatrix}0\\-1\\4\end{bmatrix}$
• 那么推广来看，我们需要考虑，对于任意的 $b$，是否都能求解 $Ax=b$？ 用列向量线性组合的观点阐述：$col_1,col_2,col_3$ 通过所有的线性组合所得到的向量 $b_i$ ，是否能够铺满整个空间？
  • 对上面这个例子，答案是肯定的。
  • 如果三个向量在同一个平面上，则无法铺满整个空间。

推广的解释：

• 当三个向量在同一个平面上时，那么他们的线性组合也一定都在这个平面上。
• 例如：$col_3=col_1+col_2$ 不管怎么组合，这三个向量的结果都逃不出其所在的平面。
• 因此当 $b$ 在平面内，方程组有解，而当 $b$ 不在平面内，这三个列向量就无法构造出 $b$。
• 在后面的课程中，我们会了解到这种情形称为奇异、矩阵不可逆。

---

2.3 更高的的维度

---

我们推广到九维空间，每个方程有九个未知数，共九个方程。

显然地，此时已经无法从坐标图像中描述问题了，但是我们依然可以从求九维列向量线性组合的角度解决问题，仍然是上面的问题。我们是否总能通过所有的线性组合所得到的向量 $b_i$，来铺满整个九维空间？

当然这仍取决于这九个向量，如果我们取一些并不相互独立的向量，则答案是否定的，比如取了九列但其实只相当于八列，有一列毫无贡献（这一列是前面列的某种线性组合），则会有一部分$b$ 无法求得。

---

2.4 关于 Ax = b 的计算

---

对于任意的线性方程组，我们都可以将其化为矩阵的形式，得到系数矩阵 $A$，向量 $x$ 和向量 $b$，接下来讲解其计算。

对于 $Ax = b$ 是一种乘法运算：

例1：

设 $A=\begin{bmatrix}2&5\\1&3\end{bmatrix},x=\begin{bmatrix}1\\2\end{bmatrix}$，求 $b$。

• 使用列向量线性组合的方式，一次计算一列，即把 $Ax$ 看做 $A$ 列向量的线性组合：

解：
$\begin{aligned} \begin{bmatrix}2&5\\1&3\end{bmatrix}\begin{bmatrix}1\\2\end{bmatrix} &= 1\begin{bmatrix}2\\1\end{bmatrix}+2\begin{bmatrix}5\\3\end{bmatrix}\\\\ &= \begin{bmatrix}1\times 2 + 2\times 5\\1\times 1 + 2\times 3\end{bmatrix}\\\\ &= \begin{bmatrix}12\\7\end{bmatrix} \end{aligned}$

---

例2：

设 $A=\begin{bmatrix}2&-1&0\\-1&2&1\\0&3&4\end{bmatrix},x=\begin{bmatrix}0\\0\\1\end{bmatrix}$，求 $b$。

解：
$\begin{aligned} \begin{bmatrix}2&-1&0\\-1&2&1\\0&3&4\end{bmatrix}\begin{bmatrix}0\\0\\1\end{bmatrix} ~~&=~~ \begin{aligned} 0\begin{bmatrix}2\\-1\\0\end{bmatrix}+0\begin{bmatrix}-1\\2\\-3\end{bmatrix}+1\begin{bmatrix}0\\-1\\4\end{bmatrix} \end{aligned}\\\\ &= \begin{bmatrix} 0\times 2 + 0\times -1 + 1\times 0\\ 0\times -1 + 0\times 2 + 1\times -1\\ 0\times 0 + 0\times -3 + 1\times 4\\ \end{bmatrix}\\\\ &= \begin{bmatrix} 1\\ -1\\ 4 \end{bmatrix} \end{aligned}$

---

3. 矩阵消元

---

这个方法最早由高斯提出，我们以前解方程组的时候都会使用，现在来看如何使用矩阵实现消元法。

---

3.1 消元法

---

有三元方程组 $\begin{cases}x&+2y&+z&=2\\3x&+8y&+z&=12\\&4y&+z&=2\end{cases}$，对应的矩阵形式 $Ax=b$ 为 $\begin{bmatrix}1&2&1\\3&8&1\\0&4&1\end{bmatrix}\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}2\\12\\2\end{bmatrix}$。

按照我们以前做消元法的思路：

• 第一步，我们希望在第二个方程中消去$x$项，来操作系数矩阵 $A=\begin{bmatrix}\underline{1}&2&1\\3&8&1\\0&4&1\end{bmatrix}$，下划线的元素为第一步的主元（pivot）：$\begin{bmatrix}\underline{1}&2&1\\3&8&1\\0&4&1\end{bmatrix}\xrightarrow{row_2-3row_1}\begin{bmatrix}\underline{1}&2&1\\0&2&-2\\0&4&1\end{bmatrix}$
  • 这里我们先不管 $b$ 向量，等做完 $A$ 的消元可以再做 $b$ 的消元。（这是MATLAB等工具经常使用的算法。）
• 第二步，我们希望在第三个方程中消去 $y$ 项，现在第二行第一个非零元素成为了第二个主元：$\begin{bmatrix}\underline{1}&2&1\\0&\underline{2}&-2\\0&4&1\end{bmatrix}\xrightarrow{row_3-2row_2}\begin{bmatrix}\underline{1}&2&1\\0&\underline{2}&-2\\0&0&\underline{5}\end{bmatrix}$
  • 注意到第三行消元过后仅剩一个非零元素，所以它就成为第三个主元。做到这里就算消元完成了。

再来讨论一下消元失效的情形：

• 首先，主元不能为零；
• 其次，如果在消元时遇到主元位置为零，则需要交换行，使主元不为零。
• 如果我们把第三个方程 $z$ 前的系数改成 $-4$，会导致第二步消元时最后一行全部为零，则第三个主元就不存在了，至此消元不能继续进行了，这就是下一讲中涉及的不可逆情况。
• 接下来就该回代（back substitution）了，这时我们在 $A$ 矩阵后面加上 $b$ 向量写成增广矩阵（augmented matrix）的形式：$\left[\begin{array}{c|c}A&b\end{array}\right]=\left[\begin{array}{ccc|c}1&2&1&2\\3&8&1&12\\0&4&1&2\end{array}\right]\to\left[\begin{array}{ccc|c}1&2&1&2\\0&2&-2&6\\0&4&1&2\end{array}\right]\to\left[\begin{array}{ccc|c}1&2&1&2\\0&2&-2&6\\0&0&5&-10\end{array}\right]$
  • 不难看出，$z$ 的解已经出现了。
• 此时方程组变为$\begin{cases}x&+2y&+z&=2\\&2y&-2z&=6\\&&5z&=-10\end{cases}$，从第三个方程求出 $z=-2$，代入第二个方程求出 $y=1$，再代入第一个方程求出 $x=2$。

---

3.2 消元矩阵

---

$2.4$ 讲我们学习了矩阵乘以向量的方法，现在有三个列向量的矩阵乘以另一个向量，按列的线性组合可以写作 $\Bigg[v_1\ v_2\ v_3\Bigg]\begin{bmatrix}3\\4\\5\end{bmatrix}=3v_1+4v_2+5v_3$。

但现在我们希望用矩阵乘法表示行操作，则有$\begin{bmatrix}1&2&7\end{bmatrix}\begin{bmatrix}&row_1&\\&row_2&\\&row_3&\end{bmatrix}=1row_1+2row_2+7row_3$。

易看出这里是一个行向量从左边乘以矩阵，这个行向量按行操作矩阵的行向量，并将其合成为一个矩阵行向量的线性组合。

介绍到这里，我们就可以将消元法所做的行操作写成向量乘以矩阵的形式了。

• 消元法第一步操作为将第二行改成 $row_2-3row_1$，其余两行不变，则有$\begin{bmatrix}1&0&0\\-3&1&0\\0&0&1\end{bmatrix}\begin{bmatrix}1&2&1\\3&8&1\\0&4&1\end{bmatrix}=\begin{bmatrix}1&2&1\\0&2&-2\\0&4&1\end{bmatrix}$
  • 对于第二行的计算 $\begin{aligned}&-3\times\begin{bmatrix}1&2&1\end{bmatrix} + 1\times\begin{bmatrix}3&8&1\end{bmatrix} + 0\times\begin{bmatrix}0&4&1\end{bmatrix} \\&= \begin{bmatrix} -3 + 3 + 0&-3\times 2 + 1\times 8 + 0&-3\times 1 + 1\times 1 + 0\end{bmatrix} \\&= \begin{bmatrix}0&2&-2\end{bmatrix}\end{aligned}$
  • 另外，如果三行都不变，消元矩阵就是单位矩阵 $I=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}$，$I$ 之于矩阵运算相当于 $1$ 之于四则运算。
  • 这个消元矩阵我们记作 $E_{21}$，即将第二行第一个元素变为零。
• 接下来就是求 $E_{32}$ 消元矩阵了，即将第三行第二个元素变为零，则$\begin{bmatrix}1&0&0\\0&1&0\\0&-2&1\end{bmatrix}\begin{bmatrix}1&2&1\\0&2&-2\\0&4&1\end{bmatrix}=\begin{bmatrix}1&2&1\\0&2&-2\\0&0&5\end{bmatrix}$。这就是消元所用的两个初等矩阵（elementary matrix）。
• 最后，我们将这两步综合起来，即 $E_{32}(E_{21}A)=U$，也就是说如果我们想从 $A$ 矩阵直接得到 $U$ 矩阵的话，只需要 $(E_{32}E_{21})A$ 即可。
  • 注意，矩阵乘法虽然不能随意变动相乘次序，但是可以变动括号位置，也就是满足结合律（associative law），而结合律在矩阵运算中非常重要，很多定理的证明都需要巧妙的使用结合律。

补充：

• 既然提到了消元用的初等矩阵，那我们再介绍一种用于置换两行的矩阵：置换矩阵（permutation matrix）。
• 例如：

$\begin{bmatrix}0&1\\1&0\end{bmatrix}\begin{bmatrix}a&b\\c&d\end{bmatrix}=\begin{bmatrix}c&d\\a&b\end{bmatrix}$，置换矩阵将原矩阵的两行做了互换。

• 顺便提一下，如果我们希望交换两列，则有$\begin{bmatrix}a&b\\c&d\end{bmatrix}\begin{bmatrix}0&1\\1&0\end{bmatrix}=\begin{bmatrix}b&a\\d&c\end{bmatrix}$。

我们现在能够将 $A$ 通过行变换写成 $U$，那么如何从 $U$ 再变回 $A$，也就是求消元的逆运算。

对某些“坏”矩阵，并没有逆，而本讲的例子都是“好”矩阵。

---

3.3 逆

---

现在，我们以 $E_{21}$ 为例，$\Bigg[\quad ?\quad \Bigg]\begin{bmatrix}1&0&0\\-3&1&0\\0&0&1\end{bmatrix}=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}$，什么矩阵可以取消这次行变换？

这次变换是从第二行中减去三倍的第一行，那么其逆变换就是给第二行加上三倍的第一行，所以逆矩阵就是$\begin{bmatrix}1&0&0\\3&1&0\\0&0&1\end{bmatrix}$。

我们把矩阵$E$的逆记作 $E^{-1}$，所以有 $E^{-1}E=I$。

---

4. 乘法和逆矩阵

---

4.1 矩阵乘法

---

4.1.1 行列内积

---

有 $m\times n$ 矩阵 $A$ 和 $n\times p$ 矩阵 $B$（$A$ 的总列数必须与 $B$ 的总行数相等），两矩阵相乘有 $AB=C$，$C$ 是一个 $m\times p$ 矩阵，对于 $C$ 矩阵中的第 $i$ 行第 $j$ 列元素 $c_{ij}$，有：

$c_{ij}=row_i\cdot column_j=\sum_{k=i}^na_{ik}b_{kj}$

其中 $a{ik}$是$A$矩阵的第$i$行第$k$列元素，$b{kj}$是$B$矩阵的第$k$行第$j$ 列元素。

可以看出 $c_{ij}$ 其实是 $A$ 矩阵第 $i$ 行点乘 $B$ 矩阵第 $j$ 列 $\begin{bmatrix}&\vdots&\\&row_i&\\&\vdots&\end{bmatrix}\begin{bmatrix}&&\\\cdots&column_j&\cdots\\&&\end{bmatrix}=\begin{bmatrix}&\vdots&\\\cdots&c_{ij}&\cdots\\&\vdots&\end{bmatrix}$

例：

设 $A=\begin{bmatrix}1&3\\2&4\\5&6\end{bmatrix},\ B=\begin{bmatrix}7&8&9\\10&11&12\end{bmatrix}$，求 $C$。

解：
$\begin{aligned} \begin{bmatrix}1&3\\2&4\\5&6\end{bmatrix}\begin{bmatrix}7&8&9\\10&11&12\end{bmatrix} ~~&=~~ \begin{bmatrix} 1\times 7+3\times 10 & 1\times 8 + 3\times 11 & 1\times9 + 3\times12\\ 2\times 7+4\times 10 & 2\times 8 + 4\times 11 & 2\times9 + 4\times12\\ 5\times 7+6\times 10 & 5\times 8 + 6\times 11 & 5\times9 +6\times12\\ \end{bmatrix}\\\\ &= \begin{bmatrix} 37&41&45\\ 54&60&66\\ 95&106&117 \end{bmatrix} \end{aligned}\begin{aligned} \end{aligned}$

---

4.1.2 整列相乘

---

上一讲我们知道了如何计算矩阵乘以向量，而整列相乘就是使用这种线性组合的思想：

$\begin{bmatrix}&&\\A_{col1}&A_{col2}&\cdots&A_{coln}\\&&\end{bmatrix}\begin{bmatrix}\cdots&b_{1j}&\cdots\\\cdots&b_{2j}&\cdots\\\cdots&\vdots&\cdots\\\cdots&b_{nj}&\cdots\\\end{bmatrix}=\begin{bmatrix}&&\\\cdots&\left(b_{1j}A_{col1}+b_{2j}A_{col2}+\cdots+b_{nj}A_{coln}\right)&\cdots\\&&\end{bmatrix}$

上面的运算为$B$的第$j$个列向量右乘矩阵 $A$，求得的结果就是 $C$ 矩阵的第 $j$ 列，即 $C$ 的第 $j$ 列是 $A$ 的列向量以 $B$ 的第 $j$ 列作为系数所求得的线性组合，$C_j=b_{1j}A_{col1}+b_{2j}A_{col2}+\cdots+b_{nj}A_{coln}$。

例：

设 $A=\begin{bmatrix}1&3\\2&4\\5&6\end{bmatrix},\ B=\begin{bmatrix}7&8&9\\10&11&12\end{bmatrix}$，求 $C$。

解：
$\begin{aligned} \begin{bmatrix}1&3\\2&4\\5&6\end{bmatrix}\begin{bmatrix}7&8&9\\10&11&12\end{bmatrix} ~~&=~~ \begin{aligned} \begin{bmatrix} 7\begin{bmatrix}1\\2\\5\end{bmatrix} + 10\begin{bmatrix}3\\4\\6\end{bmatrix}& 8\begin{bmatrix}1\\2\\5\end{bmatrix} + 11\begin{bmatrix}3\\4\\6\end{bmatrix}& 9\begin{bmatrix}1\\2\\5\end{bmatrix} + 12\begin{bmatrix}3\\4\\6\end{bmatrix} \end{bmatrix} \end{aligned}\\\\ &= \begin{bmatrix} 7\times 1+10\times 3 & 8\times 1 + 11\times 3 & 9\times 1 + 12\times 3\\ 7\times 2+10\times 4 & 8\times 2 + 11\times 4 & 9\times 2 + 12\times 4\\ 7\times 5+10\times 6 & 8\times 5 + 11\times 6 & 9\times 5 + 12\times 6\\ \end{bmatrix}\\\\ &= \begin{bmatrix} 37&41&45\\ 54&60&66\\ 95&106&117 \end{bmatrix} \end{aligned}\begin{aligned} \end{aligned}$

---

4.1.3 整行相乘

---

同样的，也是利用行向量线性组合的思想：

$\begin{bmatrix}\vdots&\vdots&\vdots&\vdots\\a_{i1}&a_{i2}&\cdots&a_{in}\\\vdots&\vdots&\vdots&\vdots\end{bmatrix}\begin{bmatrix}&B_{row1}&\\&B_{row2}&\\&\vdots&\\&B_{rown}&\end{bmatrix}=\begin{bmatrix}\vdots\\\left(a_{i1}B_{row1}+a_{i2}B_{row2}+\cdots+a_{in}B_{rown}\right)\\\vdots\end{bmatrix}$

上面的运算为$A$的第$i$个行向量左乘矩阵$B$，求得的结果就是$C$矩阵的第$i$行，即$C$的第$i$行是$B$的行向量以$A$的第$i$行作为系数所求的的线性组合，$C_i=a_{i1}B_{row1}+a_{i2}B_{row2}+\cdots+a_{in}B_{rown}$。

例：

设 $A=\begin{bmatrix}1&3\\2&4\\5&6\end{bmatrix},\ B=\begin{bmatrix}7&8&9\\10&11&12\end{bmatrix}$，求 $C$。

解：
$\begin{aligned} \begin{bmatrix}1&3\\2&4\\5&6\end{bmatrix}\begin{bmatrix}7&8&9\\10&11&12\end{bmatrix} ~~&=~~ \begin{aligned} \begin{bmatrix} 1\begin{bmatrix}7&8&9\end{bmatrix}+3\begin{bmatrix}10&11&12\end{bmatrix}\\ 2\begin{bmatrix}7&8&9\end{bmatrix}+4\begin{bmatrix}10&11&12\end{bmatrix}\\ 5\begin{bmatrix}7&8&9\end{bmatrix}+6\begin{bmatrix}10&11&12\end{bmatrix} \end{bmatrix} \end{aligned}\\\\ &= \begin{bmatrix} 1\times 7+3\times 10 & 1\times 8 + 3\times 11 & 1\times9 + 3\times12\\ 2\times 7+4\times 10 & 2\times 8 + 4\times 11 & 2\times9 + 4\times12\\ 5\times 7+6\times 10 & 5\times 8 + 6\times 11 & 5\times9 +6\times12\\ \end{bmatrix}\\\\ &= \begin{bmatrix} 37&41&45\\ 54&60&66\\ 95&106&117 \end{bmatrix} \end{aligned}$

---

4.1.4 列乘以行

---

用$A$矩阵的列乘以$B$矩阵的行，得到的矩阵相加即可：

$\begin{bmatrix}&&\\A_{col1}&A_{col2}&\cdots&A_{coln}\\&&\end{bmatrix}\begin{bmatrix}&B_{row1}&\\&B_{row2}&\\&\vdots&\\&B_{rown}&\end{bmatrix}=A_{col1}B_{row1}+A_{col2}B_{row2}+\cdots+A_{coln}B_{rown}$

注意，$A{coli}B{rowi}$是一个$m\times 1$向量乘以一个$1\times p$向量，其结果是一个$m\times p$矩阵，而所有的$m\times p$矩阵之和就是计算结果。

例：

设 $A=\begin{bmatrix}1&3\\2&4\\5&6\end{bmatrix},\ B=\begin{bmatrix}7&8&9\\10&11&12\end{bmatrix}$，求 $C$。

解：
$\begin{aligned} \begin{bmatrix}1&3\\2&4\\5&6\end{bmatrix}\begin{bmatrix}7&8&9\\10&11&12\end{bmatrix} ~~&=~~ \begin{aligned} \begin{bmatrix}1\\2\\3\end{bmatrix}\begin{bmatrix}7&8&9\end{bmatrix} + \begin{bmatrix}3\\4\\6\end{bmatrix}\begin{bmatrix}10&11&12\end{bmatrix} \end{aligned}\\\\ &= \begin{bmatrix} 1\times 7 & 1\times 8 & 1\times9\\ 2\times 7 & 2\times 8 & 2\times9\\ 5\times 7 & 5\times 8 & 5\times9 \end{bmatrix}+ \begin{bmatrix} 3\times 10 & 3\times 11 & 3\times12\\ 4\times 10 & 4\times 11 & 4\times12\\ 6\times 10 & 6\times 11 & 6\times12\\ \end{bmatrix}\\\\ &= \begin{bmatrix} 7 & 8 & 9\\ 14 & 16 & 18\\ 35 & 40 & 45 \end{bmatrix}+ \begin{bmatrix} 30 & 33 & 36\\ 40 & 44 & 48\\ 60 & 66 & 72\\ \end{bmatrix}\\\\ &= \begin{bmatrix} 37&41&45\\ 54&60&66\\ 95&106&117 \end{bmatrix} \end{aligned}$

---

4.1.5 分块乘法

---

$\left[\begin{array}{c|c}A_1&A_2\\\hline A_3&A_4\end{array}\right]\left[\begin{array}{c|c}B_1&B_2\\\hline B_3&B_4\end{array}\right]=\left[\begin{array}{c|c}A_1B_1+A_2B_3&A_1B_2+A_2B_4\\\hline A_3B_1+A_4B_3&A_3B_2+A_4B_4\end{array}\right]$

在分块合适的情况下，可以简化运算。

---

4.2 逆（方阵）

---

4.2.1 概念

---

• 首先，并不是所有的方阵都有逆；而如果逆存在，则有 $A^{-1}A=I=AA^{-1}$。
• 对于方阵，左逆和右逆是相等的，但是对于非方阵（长方形矩阵），其左逆不等于右逆。
• 对于这些有逆的矩阵，我们称其为可逆的或非奇异的。

---

4.2.2 可逆的判断

---

我们先来看看奇异矩阵（不可逆的）：$A=\begin{bmatrix}1&2\\3&6\end{bmatrix}$，在后面将要学习的行列式中，会发现这个矩阵的行列式为 $0$。

• 观察这个方阵，我们如果用另一个矩阵乘 $A$，则得到的结果矩阵中的每一列应该都是 $\begin{bmatrix}1\\2\end{bmatrix}$ 的倍数，所以我们不可能从 $AB$ 的乘积中得到单位矩阵 $I$。
• 另一种判定方法，如果存在非零向量 $x$，使得 $Ax=0$，则矩阵 $A$ 不可逆。

我们来用上面的矩阵为例：$\begin{bmatrix}1&2\\3&6\end{bmatrix}\begin{bmatrix}3\\-1\end{bmatrix}=\begin{bmatrix}0\\0\end{bmatrix}$。

• 证明：如果对于非零的 $x$ 仍有 $Ax=0$，而 $A$ 有逆 $A^{-1}$，则 $A^{-1}Ax=0$，即 $x=0$，与题设矛盾，得证。

现在来看看什么矩阵有逆，设 $A=\begin{bmatrix}1&3\\2&7\end{bmatrix}$，我们来求 $A^{-1}$。$\begin{bmatrix}1&3\\2&7\end{bmatrix}\begin{bmatrix}a&b\\c&d\end{bmatrix}=\begin{bmatrix}1&0\\0&1\end{bmatrix}$，使用列向量线性组合的思想，我们可以说 $A$ 乘以 $A^{-1}$ 的第 $j$ 列，能够得到 $I$ 的第 $j$ 列，这时我们会得到一个关于列的方程组。

---

4.2.3 逆矩阵的求法

---

接下来介绍（Gauss-Jordan）方法，该方法可以一次处理所有的方程：

• 这个方程组为$\begin{cases}\begin{bmatrix}1&3\\2&7\end{bmatrix}\begin{bmatrix}a\\b\end{bmatrix}=\begin{bmatrix}1\\0\end{bmatrix}\\\\\begin{bmatrix}1&3\\2&7\end{bmatrix}\begin{bmatrix}c\\d\end{bmatrix}=\begin{bmatrix}0\\1\end{bmatrix}\end{cases}$，我们想要同时解这两个方程；

• 构造这样一个矩阵$\left[\begin{array}{cc|cc}1&3&1&0\\2&7&0&1\end{array}\right]$，接下来用消元法将左侧变为单位矩阵；

• $\left[\begin{array}{cc|cc}1&3&1&0\\2&7&0&1\end{array}\right]\xrightarrow{row_2-2row_1}\left[\begin{array}{cc|cc}1&3&1&0\\0&1&-2&1\end{array}\right]\xrightarrow{row_1-3row_2}\left[\begin{array}{cc|cc}1&0&7&-3\\0&1&-2&1\end{array}\right]$

• 于是，我们就将矩阵从$\left[\begin{array}{c|c}A&I\end{array}\right]$ 变为 $\left[\begin{array}{c|c}I&A^{-1}\end{array}\right]$

该方法的本质是使用消元矩阵 $E$，对 $A$ 进行操作，$E\left[\begin{array}{c|c}A&I\end{array}\right]$，利用一步步消元有 $EA=I$，进而得到 $\left[\begin{array}{c|c}I&E\end{array}\right]$，其实这个消元矩阵 $E$ 就是 $A^{-1}$，而 $I$ 只是负责记录消元的每一步操作，待消元完成，逆矩阵就自然出现了。