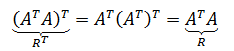1. 基本概念
1.1 行列式
二阶行列式:
\[\left|\begin{matrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{matrix}\right| = a_{11}\times a_{12} - a_{21}\times a_{22}\]- 对于 $a_{ij}$:$i$ 表示行标,$j$ 表示列标。
- 对角线 \[a_{11}a_{22}\] 为主对角线;\[a_{12}a_{21}\] 为次对角线
三阶行列式:
\[\left|\begin{matrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33} \end{matrix}\right| = \begin{aligned}&a_{11}\times a_{22}\times a_{33} + a_{21}\times a_{32}\times a_{33} + a_{12}\times a_{23}\times a_{31}\\&-a_{13}\times a_{22}\times a_{31} - a_{23}\times a_{32}\times a_{11} - a_{12}\times a_{21}\times a_{33}\end{aligned}\]1.2 线性方程组
$n$ 元非齐次线性方程组:
- 设有 $n$ 个未知数 $m$ 个方程的线性方程组,其中 $a_{ij}$ 是第 $i$ 个方程第 $j$ 个未知数的系数,$b_i$ 是第 $i$ 个方程的常数项,且 $b_i$ 不全为 $0$。
\begin{cases}
a_{11}x_1+a_{12}x_2+\dots+a_{1n}x_n=b_1\\\\
a_{21}x_1+a_{22}x_2+\dots+a_{2n}x_n=b_2\\\\
\dots\\\\
a_{n1}x_1+a_{n2}x_2+\dots+a_{nn}x_n=b_n\\
\end{cases}\\
\]
$n$ 元齐次线性方程组:
- 设有 $n$ 个未知数 $m$ 个方程的线性方程组,其中 $a_{ij}$ 是第 $i$ 个方程第 $j$ 个未知数的系数,$b_i$ 是第 $i$ 个方程的常数项,且 $b_i = 0$。
\begin{cases}
a_{11}x_1+a_{12}x_2+\dots+a_{1n}x_n=0\\\\
a_{21}x_1+a_{22}x_2+\dots+a_{2n}x_n=0\\\\
\dots\\\\
a_{n1}x_1+a_{n2}x_2+\dots+a_{nn}x_n=0\\
\end{cases}\\
\]
线性方程组:
- $n$ 元线性方程组简称线性方程组或方程组。
1.3 矩阵
1.3.1 矩阵的定义
二阶矩阵:
\[\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}\]三阶矩阵:
\[\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33} \end{bmatrix} \]$m\times n$ 矩阵:
- 由 $m\times n$ 个数 $a_{ij}(i = 1, 2, \dots, m, j = 1, 2, \dots,n)$ 排列成的 $m$ 行 $n$ 列的数表。
A =
\begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1 n} \\
a_{21} & a_{22} & \cdots & a_{2 n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m 1} & a_{m 2} & \cdots & a_{m n}
\end{bmatrix}
\]
与线性方程组相关的矩阵:
对于非齐次线性方程组:
\[
\begin{cases}
a_{11}x_1+a_{12}x_2+\dots+a_{1n}x_n=b_1\\\\
a_{21}x_1+a_{22}x_2+\dots+a_{2n}x_n=b_2\\\\
\dots\\\\
a_{n1}x_1+a_{n2}x_2+\dots+a_{nn}x_n=b_n\\
\end{cases}\\
\]
有如下矩阵:
\[
A = \begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1 n} \\
a_{21} & a_{22} & \cdots & a_{2 n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m 1} & a_{m 2} & \cdots & a_{m n}
\end{bmatrix},
X = \begin{bmatrix}x_1\\x_2\\\vdots\\x_n\end{bmatrix},
b = \begin{bmatrix}b_1\\b_2\\\vdots\\b_n\end{bmatrix},
B = \begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1 n} &b_{1}\\
a_{21} & a_{22} & \cdots & a_{2 n} &b_{2}\\
\vdots & \vdots & \ddots & \vdots &\vdots\\
a_{m 1} & a_{m 2} & \cdots & a_{m n}&b_{m}\\
\end{bmatrix}
\]
其中:
- $A$ 为系数矩阵。
- $X$ 为未知数矩阵。
- $b$ 为常数项矩阵。
- $B$ 为增广矩阵。
1.3.2 矩阵的计算
加减:
- 两个矩阵相加或相减,需要满足两个矩阵的列数和行数一致。
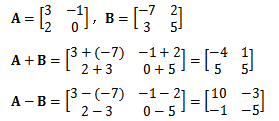
- 满足交换律: $A + B = B + A$
乘法:
- 两个矩阵 $A$ 和 $B$ 相乘,需要满足 $A$ 的列数等于 $B$ 的行数。
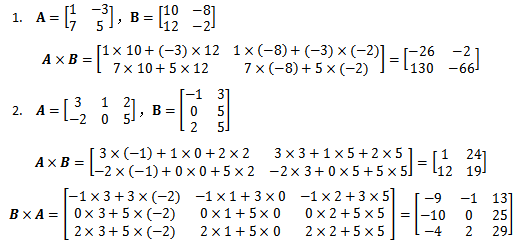
- 矩阵乘法不满足交换律:$AB\ne BA $,但仍然满足结合律和分配律:
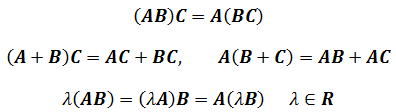
1.3.3 零矩阵和单位矩阵
零矩阵:
- 元素都是 $0$ 的矩阵称为零矩阵,记作 $O$。
- 不同型的零矩阵是不同的。
单位矩阵:
- 单位矩阵是一个 $n\times n$ 矩阵,从左到右的对角线(主对角线)上的元素是 $1$,其余元素都为 $0$。
下面是三个单位矩阵:

- 若矩阵 $A$ 为 $n\times n$ 的方阵,$E$ 为单位矩阵,则:$AE=A,EA=A$
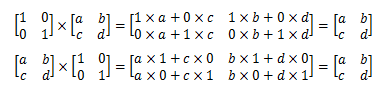
1.3.4 逆矩阵和奇异矩阵
逆矩阵:
- 矩阵 $A$ 的逆矩阵记作 $A^{-1}$。
- $AA^{-1} = E$,其中 $E$ 为单位矩阵。

奇异矩阵:
- 当一个矩阵没有逆矩阵的时候,称该矩阵为奇异矩阵。
- 当且仅当一个矩阵的行列式为零时,该矩阵是奇异矩阵。
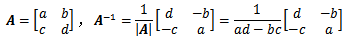
当 $a\times d-b\times c=0$ 时 $A$ 没有定义,$A^{-1}$不存在,则 $A$ 是奇异矩阵。
如 :\[A=\begin{bmatrix}1&1\\2&2\end{bmatrix}\] 是奇异矩阵。
1.3.5 矩阵转置
- 将矩阵 $A$ 的行换成同序数的列得到的新的矩阵,叫做 $A$ 的转置矩阵,记作: $A^T$。
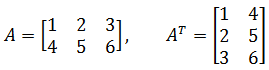
- 转置运算公式:
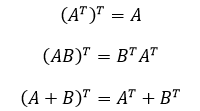
1.3.6 对称矩阵
- 如果一个矩阵转置后等于原矩阵,那么这个矩阵称为对称矩阵。
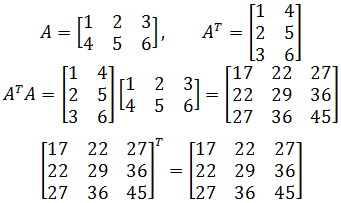
-
由定义可知,对称矩阵一定是方阵。
-
对称矩阵很常见,实际上,一个矩阵转置和这个矩阵的乘积就是一个对称矩阵:
-
两个对称矩阵相加,仍然得到对称矩阵:
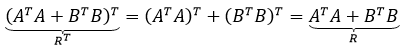
2. 方程组的解释
2.1 二元方程组及其矩阵
设方程组有 $2$ 个未知数,一共有 $2$ 个方程:
- 则有方程组 \[\begin{cases}2x&-y&=0\\-x&+2y&=3\end{cases}\]
- 写作矩阵形式有 \[\begin{bmatrix}2&-1\\-1&2\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}0\\3\end{bmatrix}\]
通常我们把第一个矩阵称为系数矩阵 $A$,将第二个矩阵称为向量 $x$,将第三个矩阵称为向量 $b$,于是线性方程组可以表示为 $Ax=b$。
行图像:
- 即直角坐标系中的图像。
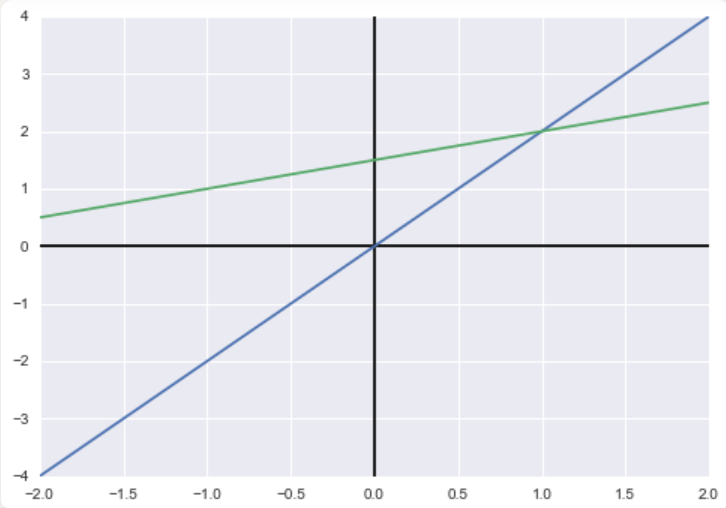
解释:
- 上图是直角坐标系中方程组中的两直线相交的情况。
- 接下来我们按列观察方程组:
- \[x\begin{bmatrix}2\\-1\end{bmatrix}+y\begin{bmatrix}-1\\2\end{bmatrix}=\begin{bmatrix}0\\3\end{bmatrix}\]
- 我们把第一个向量称作 $col_1$,第二个向量称作 $col_2$,分别表示第一列的向量和第二列的向量。
- 要使得式子成立需要第一个向量加上两倍的第二个向量,即:
- \[1\times col_1 + 2\times col_2 = 1\begin{bmatrix}2\\-1\end{bmatrix}+2\begin{bmatrix}-1\\2\end{bmatrix}=\begin{bmatrix}0\\3\end{bmatrix}\]
- 这和我们方程组的解 $x = 1,y = 2$ 是对应的。
列图像:
- 即在二维平面上画出上面的列向量。
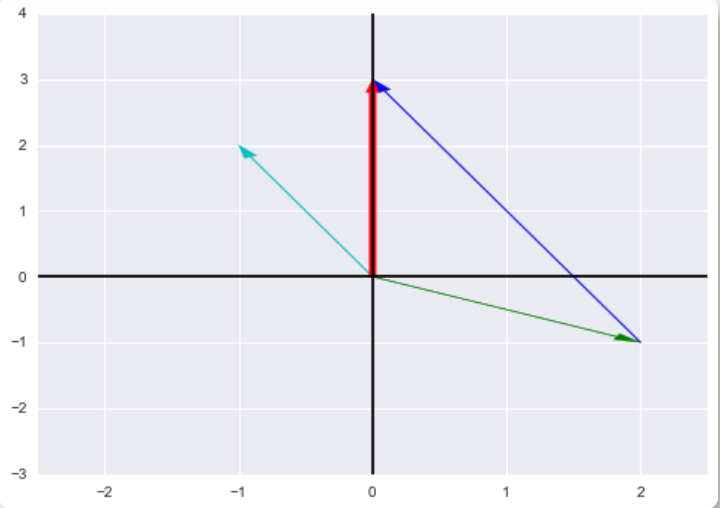
解释:
- 绿向量 $col_1$与蓝向量(两倍的绿向量 $col_2$)合成红向量 $b$。
- 接下来我们继续观察方程组:
- \[x\begin{bmatrix}2\\-1\end{bmatrix}+y\begin{bmatrix}-1\\2\end{bmatrix}=\begin{bmatrix}0\\3\end{bmatrix}\]
- 显然地,$col_1$ 和 $col_2$ 通过某种线性组合得到了向量 $b$,即:
- \[1\times col_1 + 2\times col_2 = 1\begin{bmatrix}2\\-1\end{bmatrix}+2\begin{bmatrix}-1\\2\end{bmatrix}=\begin{bmatrix}0\\3\end{bmatrix}\]
- 那么推广来看, $col_1$ 和 $col_2$ 通过所有的线性组合所得到的向量 $b_i$ 将能够铺满整个平面。
2.2 三元方程组及其矩阵
设方程组有 $3$ 个未知数,一共有 $3$ 个方程:
- 则有方程组 \[\begin{cases}2x&-y&&=0\\-x&+2y&-z&=-1\\&-3y&+4z&=4\end{cases}\]
- 写作矩阵形式有 \[A=\begin{bmatrix}2&-1&0\\-1&2&-1\\0&-3&4\end{bmatrix},\\ b=\begin{bmatrix}0\\-1\\4\end{bmatrix}\]
行图像的解释:
- 在三维直角坐标系中,每一个方程将确定一个平面。
- 接下来我们按列观察方程组:
- \[x\begin{bmatrix}2\\-1\\0\end{bmatrix}+y\begin{bmatrix}-1\\2\\-3\end{bmatrix}+z\begin{bmatrix}0\\-1\\4\end{bmatrix}=\begin{bmatrix}0\\-1\\4\end{bmatrix}\]
- 该例子中的三个平面会相交于一点 $(0,0,1)$,这个点就是方程组的解,且带入 $x = 0,y = 0,z = 1$ 也可以使得上述式子成立。
列图像的解释:
- 观察列图像的向量 $col_1,col_2,col3$ 的组合。
- 继续观察方程组:
- \[x\begin{bmatrix}2\\-1\\0\end{bmatrix}+y\begin{bmatrix}-1\\2\\-3\end{bmatrix}+z\begin{bmatrix}0\\-1\\4\end{bmatrix}=\begin{bmatrix}0\\-1\\4\end{bmatrix}\]
- 显然地,$col_1,col_2,col_3$ 也可以通过某种线性组合得到向量 $b$,即:
- \[0\times col_1 + 0\times col_2 + 1\times col_3= 0\begin{bmatrix}2\\-1\\0\end{bmatrix}+0\begin{bmatrix}-1\\2\\-3\end{bmatrix}+1\begin{bmatrix}0\\-1\\4\end{bmatrix}=\begin{bmatrix}0\\-1\\4\end{bmatrix}\]
- 那么推广来看,我们需要考虑,对于任意的 $b$,是否都能求解 $Ax=b$? 用列向量线性组合的观点阐述:$col_1,col_2,col_3$ 通过所有的线性组合所得到的向量 $b_i$ ,是否能够铺满整个空间?
- 对上面这个例子,答案是肯定的。
- 如果三个向量在同一个平面上,则无法铺满整个空间。
推广的解释:
- 当三个向量在同一个平面上时,那么他们的线性组合也一定都在这个平面上。
- 例如:$col_3=col_1+col_2$ 不管怎么组合,这三个向量的结果都逃不出其所在的平面。
- 因此当 $b$ 在平面内,方程组有解,而当 $b$ 不在平面内,这三个列向量就无法构造出 $b$。
- 在后面的课程中,我们会了解到这种情形称为奇异、矩阵不可逆。
2.3 更高的的维度
我们推广到九维空间,每个方程有九个未知数,共九个方程。
显然地,此时已经无法从坐标图像中描述问题了,但是我们依然可以从求九维列向量线性组合的角度解决问题,仍然是上面的问题。我们是否总能通过所有的线性组合所得到的向量 $b_i$,来铺满整个九维空间?
当然这仍取决于这九个向量,如果我们取一些并不相互独立的向量,则答案是否定的,比如取了九列但其实只相当于八列,有一列毫无贡献(这一列是前面列的某种线性组合),则会有一部分$b$ 无法求得。
2.4 关于 Ax = b 的计算
对于任意的线性方程组,我们都可以将其化为矩阵的形式,得到系数矩阵 $A$,向量 $x$ 和向量 $b$,接下来讲解其计算。
对于 $Ax = b$ 是一种乘法运算:
例1:
设 \[A=\begin{bmatrix}2&5\\1&3\end{bmatrix},x=\begin{bmatrix}1\\2\end{bmatrix}\],求 $b$。
- 使用列向量线性组合的方式,一次计算一列,即把 $Ax$ 看做 $A$ 列向量的线性组合:
解:
\[
\begin{aligned}
\begin{bmatrix}2&5\\1&3\end{bmatrix}\begin{bmatrix}1\\2\end{bmatrix}
&=
1\begin{bmatrix}2\\1\end{bmatrix}+2\begin{bmatrix}5\\3\end{bmatrix}\\\\
&=
\begin{bmatrix}1\times 2 + 2\times 5\\1\times 1 + 2\times 3\end{bmatrix}\\\\
&=
\begin{bmatrix}12\\7\end{bmatrix}
\end{aligned}
\]
例2:
设 \[A=\begin{bmatrix}2&-1&0\\-1&2&1\\0&3&4\end{bmatrix},x=\begin{bmatrix}0\\0\\1\end{bmatrix}\],求 $b$。
解:
\[
\begin{aligned}
\begin{bmatrix}2&-1&0\\-1&2&1\\0&3&4\end{bmatrix}\begin{bmatrix}0\\0\\1\end{bmatrix}
~~&=~~
\begin{aligned}
0\begin{bmatrix}2\\-1\\0\end{bmatrix}+0\begin{bmatrix}-1\\2\\-3\end{bmatrix}+1\begin{bmatrix}0\\-1\\4\end{bmatrix}
\end{aligned}\\\\
&=
\begin{bmatrix}
0\times 2 + 0\times -1 + 1\times 0\\
0\times -1 + 0\times 2 + 1\times -1\\
0\times 0 + 0\times -3 + 1\times 4\\
\end{bmatrix}\\\\
&=
\begin{bmatrix}
1\\
-1\\
4
\end{bmatrix}
\end{aligned}
\]
3. 矩阵消元
这个方法最早由高斯提出,我们以前解方程组的时候都会使用,现在来看如何使用矩阵实现消元法。
3.1 消元法
有三元方程组 \[\begin{cases}x&+2y&+z&=2\\3x&+8y&+z&=12\\&4y&+z&=2\end{cases}\],对应的矩阵形式 $Ax=b$ 为 \[\begin{bmatrix}1&2&1\\3&8&1\\0&4&1\end{bmatrix}\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}2\\12\\2\end{bmatrix}\]。
按照我们以前做消元法的思路:
- 第一步,我们希望在第二个方程中消去$x$项,来操作系数矩阵 \[A=\begin{bmatrix}\underline{1}&2&1\\3&8&1\\0&4&1\end{bmatrix}\],下划线的元素为第一步的主元(pivot):\[\begin{bmatrix}\underline{1}&2&1\\3&8&1\\0&4&1\end{bmatrix}\xrightarrow{row_2-3row_1}\begin{bmatrix}\underline{1}&2&1\\0&2&-2\\0&4&1\end{bmatrix}\]
- 这里我们先不管 $b$ 向量,等做完 $A$ 的消元可以再做 $b$ 的消元。(这是
MATLAB等工具经常使用的算法。)
- 这里我们先不管 $b$ 向量,等做完 $A$ 的消元可以再做 $b$ 的消元。(这是
- 第二步,我们希望在第三个方程中消去 $y$ 项,现在第二行第一个非零元素成为了第二个主元:\[\begin{bmatrix}\underline{1}&2&1\\0&\underline{2}&-2\\0&4&1\end{bmatrix}\xrightarrow{row_3-2row_2}\begin{bmatrix}\underline{1}&2&1\\0&\underline{2}&-2\\0&0&\underline{5}\end{bmatrix}\]
- 注意到第三行消元过后仅剩一个非零元素,所以它就成为第三个主元。做到这里就算消元完成了。
再来讨论一下消元失效的情形:
- 首先,主元不能为零;
- 其次,如果在消元时遇到主元位置为零,则需要交换行,使主元不为零。
- 如果我们把第三个方程 $z$ 前的系数改成 $-4$,会导致第二步消元时最后一行全部为零,则第三个主元就不存在了,至此消元不能继续进行了,这就是下一讲中涉及的不可逆情况。
- 接下来就该回代(back substitution)了,这时我们在 $A$ 矩阵后面加上 $b$ 向量写成增广矩阵(augmented matrix)的形式:\[\left[\begin{array}{c|c}A&b\end{array}\right]=\left[\begin{array}{ccc|c}1&2&1&2\\3&8&1&12\\0&4&1&2\end{array}\right]\to\left[\begin{array}{ccc|c}1&2&1&2\\0&2&-2&6\\0&4&1&2\end{array}\right]\to\left[\begin{array}{ccc|c}1&2&1&2\\0&2&-2&6\\0&0&5&-10\end{array}\right]\]
- 不难看出,$z$ 的解已经出现了。
- 此时方程组变为\[\begin{cases}x&+2y&+z&=2\\&2y&-2z&=6\\&&5z&=-10\end{cases}\],从第三个方程求出 $z=-2$,代入第二个方程求出 $y=1$,再代入第一个方程求出 $x=2$。
3.2 消元矩阵
$2.4$ 讲我们学习了矩阵乘以向量的方法,现在有三个列向量的矩阵乘以另一个向量,按列的线性组合可以写作 \[\Bigg[v_1\ v_2\ v_3\Bigg]\begin{bmatrix}3\\4\\5\end{bmatrix}=3v_1+4v_2+5v_3\]。
但现在我们希望用矩阵乘法表示行操作,则有\[\begin{bmatrix}1&2&7\end{bmatrix}\begin{bmatrix}&row_1&\\&row_2&\\&row_3&\end{bmatrix}=1row_1+2row_2+7row_3\]。
易看出这里是一个行向量从左边乘以矩阵,这个行向量按行操作矩阵的行向量,并将其合成为一个矩阵行向量的线性组合。
介绍到这里,我们就可以将消元法所做的行操作写成向量乘以矩阵的形式了。
- 消元法第一步操作为将第二行改成 $row_2-3row_1$,其余两行不变,则有\[\begin{bmatrix}1&0&0\\-3&1&0\\0&0&1\end{bmatrix}\begin{bmatrix}1&2&1\\3&8&1\\0&4&1\end{bmatrix}=\begin{bmatrix}1&2&1\\0&2&-2\\0&4&1\end{bmatrix}\]
- 对于第二行的计算 \[\begin{aligned}&-3\times\begin{bmatrix}1&2&1\end{bmatrix} + 1\times\begin{bmatrix}3&8&1\end{bmatrix} + 0\times\begin{bmatrix}0&4&1\end{bmatrix} \\&= \begin{bmatrix} -3 + 3 + 0&-3\times 2 + 1\times 8 + 0&-3\times 1 + 1\times 1 + 0\end{bmatrix} \\&= \begin{bmatrix}0&2&-2\end{bmatrix}\end{aligned}\]
- 另外,如果三行都不变,消元矩阵就是单位矩阵 \[I=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}\],$I$ 之于矩阵运算相当于 $1$ 之于四则运算。
- 这个消元矩阵我们记作 $E_{21}$,即将第二行第一个元素变为零。
- 接下来就是求 $E_{32}$ 消元矩阵了,即将第三行第二个元素变为零,则\[\begin{bmatrix}1&0&0\\0&1&0\\0&-2&1\end{bmatrix}\begin{bmatrix}1&2&1\\0&2&-2\\0&4&1\end{bmatrix}=\begin{bmatrix}1&2&1\\0&2&-2\\0&0&5\end{bmatrix}\]。这就是消元所用的两个初等矩阵(elementary matrix)。
- 最后,我们将这两步综合起来,即 \[E_{32}(E_{21}A)=U\],也就是说如果我们想从 $A$ 矩阵直接得到 $U$ 矩阵的话,只需要 \[(E_{32}E_{21})A\] 即可。
- 注意,矩阵乘法虽然不能随意变动相乘次序,但是可以变动括号位置,也就是满足结合律(associative law),而结合律在矩阵运算中非常重要,很多定理的证明都需要巧妙的使用结合律。
补充:
- 既然提到了消元用的初等矩阵,那我们再介绍一种用于置换两行的矩阵:置换矩阵(permutation matrix)。
- 例如:
\[\begin{bmatrix}0&1\\1&0\end{bmatrix}\begin{bmatrix}a&b\\c&d\end{bmatrix}=\begin{bmatrix}c&d\\a&b\end{bmatrix}\],置换矩阵将原矩阵的两行做了互换。
- 顺便提一下,如果我们希望交换两列,则有\[\begin{bmatrix}a&b\\c&d\end{bmatrix}\begin{bmatrix}0&1\\1&0\end{bmatrix}=\begin{bmatrix}b&a\\d&c\end{bmatrix}\]。
我们现在能够将 $A$ 通过行变换写成 $U$,那么如何从 $U$ 再变回 $A$,也就是求消元的逆运算。
对某些“坏”矩阵,并没有逆,而本讲的例子都是“好”矩阵。
3.3 逆
现在,我们以 $E_{21}$ 为例,\[\Bigg[\quad ?\quad \Bigg]\begin{bmatrix}1&0&0\\-3&1&0\\0&0&1\end{bmatrix}=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}\],什么矩阵可以取消这次行变换?
这次变换是从第二行中减去三倍的第一行,那么其逆变换就是给第二行加上三倍的第一行,所以逆矩阵就是\[\begin{bmatrix}1&0&0\\3&1&0\\0&0&1\end{bmatrix}\]。
我们把矩阵$E$的逆记作 $E^{-1}$,所以有 $E^{-1}E=I$。
4. 乘法和逆矩阵
4.1 矩阵乘法
4.1.1 行列内积
有 $m\times n$ 矩阵 $A$ 和 $n\times p$ 矩阵 $B$($A$ 的总列数必须与 $B$ 的总行数相等),两矩阵相乘有 $AB=C$,$C$ 是一个 $m\times p$ 矩阵,对于 $C$ 矩阵中的第 $i$ 行第 $j$ 列元素 $c_{ij}$,有:
\[c_{ij}=row_i\cdot column_j=\sum_{k=i}^na_{ik}b_{kj}\]其中 $a{ik}$ 是 $A$ 矩阵的第 $i$ 行第 $k$ 列元素,$b{kj}$ 是 $B$ 矩阵的第 $k$ 行第 $j$ 列元素。
可以看出 $c_{ij}$ 其实是 $A$ 矩阵第 $i$ 行点乘 $B$ 矩阵第 $j$ 列 \[\begin{bmatrix}&\vdots&\\&row_i&\\&\vdots&\end{bmatrix}\begin{bmatrix}&&\\\cdots&column_j&\cdots\\&&\end{bmatrix}=\begin{bmatrix}&\vdots&\\\cdots&c_{ij}&\cdots\\&\vdots&\end{bmatrix}\]
例:
设 \[A=\begin{bmatrix}1&3\\2&4\\5&6\end{bmatrix},\ B=\begin{bmatrix}7&8&9\\10&11&12\end{bmatrix}\],求 $C$。
解:
\[
\begin{aligned}
\begin{bmatrix}1&3\\2&4\\5&6\end{bmatrix}\begin{bmatrix}7&8&9\\10&11&12\end{bmatrix}
~~&=~~
\begin{bmatrix}
1\times 7+3\times 10 & 1\times 8 + 3\times 11 & 1\times9 + 3\times12\\
2\times 7+4\times 10 & 2\times 8 + 4\times 11 & 2\times9 + 4\times12\\
5\times 7+6\times 10 & 5\times 8 + 6\times 11 & 5\times9 +6\times12\\
\end{bmatrix}\\\\
&=
\begin{bmatrix}
37&41&45\\
54&60&66\\
95&106&117
\end{bmatrix}
\end{aligned}\begin{aligned}
\end{aligned}
\]
4.1.2 整列相乘
上一讲我们知道了如何计算矩阵乘以向量,而整列相乘就是使用这种线性组合的思想:
\[\begin{bmatrix}&&\\A_{col1}&A_{col2}&\cdots&A_{coln}\\&&\end{bmatrix}\begin{bmatrix}\cdots&b_{1j}&\cdots\\\cdots&b_{2j}&\cdots\\\cdots&\vdots&\cdots\\\cdots&b_{nj}&\cdots\\\end{bmatrix}=\begin{bmatrix}&&\\\cdots&\left(b_{1j}A_{col1}+b_{2j}A_{col2}+\cdots+b_{nj}A_{coln}\right)&\cdots\\&&\end{bmatrix}\]上面的运算为$B$的第$j$个列向量右乘矩阵 $A$,求得的结果就是 $C$ 矩阵的第 $j$ 列,即 $C$ 的第 $j$ 列是 $A$ 的列向量以 $B$ 的第 $j$ 列作为系数所求得的线性组合,\[C_j=b_{1j}A_{col1}+b_{2j}A_{col2}+\cdots+b_{nj}A_{coln}\]。
例:
设 \[A=\begin{bmatrix}1&3\\2&4\\5&6\end{bmatrix},\ B=\begin{bmatrix}7&8&9\\10&11&12\end{bmatrix}\],求 $C$。
解:
\[
\begin{aligned}
\begin{bmatrix}1&3\\2&4\\5&6\end{bmatrix}\begin{bmatrix}7&8&9\\10&11&12\end{bmatrix}
~~&=~~
\begin{aligned}
\begin{bmatrix}
7\begin{bmatrix}1\\2\\5\end{bmatrix} + 10\begin{bmatrix}3\\4\\6\end{bmatrix}&
8\begin{bmatrix}1\\2\\5\end{bmatrix} + 11\begin{bmatrix}3\\4\\6\end{bmatrix}&
9\begin{bmatrix}1\\2\\5\end{bmatrix} + 12\begin{bmatrix}3\\4\\6\end{bmatrix}
\end{bmatrix}
\end{aligned}\\\\
&=
\begin{bmatrix}
7\times 1+10\times 3 & 8\times 1 + 11\times 3 & 9\times 1 + 12\times 3\\
7\times 2+10\times 4 & 8\times 2 + 11\times 4 & 9\times 2 + 12\times 4\\
7\times 5+10\times 6 & 8\times 5 + 11\times 6 & 9\times 5 + 12\times 6\\
\end{bmatrix}\\\\
&=
\begin{bmatrix}
37&41&45\\
54&60&66\\
95&106&117
\end{bmatrix}
\end{aligned}\begin{aligned}
\end{aligned}
\]
4.1.3 整行相乘
同样的,也是利用行向量线性组合的思想:
\[\begin{bmatrix}\vdots&\vdots&\vdots&\vdots\\a_{i1}&a_{i2}&\cdots&a_{in}\\\vdots&\vdots&\vdots&\vdots\end{bmatrix}\begin{bmatrix}&B_{row1}&\\&B_{row2}&\\&\vdots&\\&B_{rown}&\end{bmatrix}=\begin{bmatrix}\vdots\\\left(a_{i1}B_{row1}+a_{i2}B_{row2}+\cdots+a_{in}B_{rown}\right)\\\vdots\end{bmatrix}\]上面的运算为$A$的第$i$个行向量左乘矩阵$B$,求得的结果就是$C$矩阵的第$i$行,即$C$的第$i$行是$B$的行向量以$A$的第$i$行作为系数所求的的线性组合,\[C_i=a_{i1}B_{row1}+a_{i2}B_{row2}+\cdots+a_{in}B_{rown}\]。
例:
设 \[A=\begin{bmatrix}1&3\\2&4\\5&6\end{bmatrix},\ B=\begin{bmatrix}7&8&9\\10&11&12\end{bmatrix}\],求 $C$。
解:
\[
\begin{aligned}
\begin{bmatrix}1&3\\2&4\\5&6\end{bmatrix}\begin{bmatrix}7&8&9\\10&11&12\end{bmatrix}
~~&=~~
\begin{aligned}
\begin{bmatrix}
1\begin{bmatrix}7&8&9\end{bmatrix}+3\begin{bmatrix}10&11&12\end{bmatrix}\\
2\begin{bmatrix}7&8&9\end{bmatrix}+4\begin{bmatrix}10&11&12\end{bmatrix}\\
5\begin{bmatrix}7&8&9\end{bmatrix}+6\begin{bmatrix}10&11&12\end{bmatrix}
\end{bmatrix}
\end{aligned}\\\\
&=
\begin{bmatrix}
1\times 7+3\times 10 & 1\times 8 + 3\times 11 & 1\times9 + 3\times12\\
2\times 7+4\times 10 & 2\times 8 + 4\times 11 & 2\times9 + 4\times12\\
5\times 7+6\times 10 & 5\times 8 + 6\times 11 & 5\times9 +6\times12\\
\end{bmatrix}\\\\
&=
\begin{bmatrix}
37&41&45\\
54&60&66\\
95&106&117
\end{bmatrix}
\end{aligned}
\]
4.1.4 列乘以行
用$A$矩阵的列乘以$B$矩阵的行,得到的矩阵相加即可:
\[\begin{bmatrix}&&\\A_{col1}&A_{col2}&\cdots&A_{coln}\\&&\end{bmatrix}\begin{bmatrix}&B_{row1}&\\&B_{row2}&\\&\vdots&\\&B_{rown}&\end{bmatrix}=A_{col1}B_{row1}+A_{col2}B_{row2}+\cdots+A_{coln}B_{rown}\]注意,$A{coli}B{rowi}$是一个$m\times 1$向量乘以一个$1\times p$向量,其结果是一个$m\times p$矩阵,而所有的$m\times p$矩阵之和就是计算结果。
例:
设 \[A=\begin{bmatrix}1&3\\2&4\\5&6\end{bmatrix},\ B=\begin{bmatrix}7&8&9\\10&11&12\end{bmatrix}\],求 $C$。
解:
\[
\begin{aligned}
\begin{bmatrix}1&3\\2&4\\5&6\end{bmatrix}\begin{bmatrix}7&8&9\\10&11&12\end{bmatrix}
~~&=~~
\begin{aligned}
\begin{bmatrix}1\\2\\3\end{bmatrix}\begin{bmatrix}7&8&9\end{bmatrix} +
\begin{bmatrix}3\\4\\6\end{bmatrix}\begin{bmatrix}10&11&12\end{bmatrix}
\end{aligned}\\\\
&=
\begin{bmatrix}
1\times 7 & 1\times 8 & 1\times9\\
2\times 7 & 2\times 8 & 2\times9\\
5\times 7 & 5\times 8 & 5\times9
\end{bmatrix}+
\begin{bmatrix}
3\times 10 & 3\times 11 & 3\times12\\
4\times 10 & 4\times 11 & 4\times12\\
6\times 10 & 6\times 11 & 6\times12\\
\end{bmatrix}\\\\
&=
\begin{bmatrix}
7 & 8 & 9\\
14 & 16 & 18\\
35 & 40 & 45
\end{bmatrix}+
\begin{bmatrix}
30 & 33 & 36\\
40 & 44 & 48\\
60 & 66 & 72\\
\end{bmatrix}\\\\
&=
\begin{bmatrix}
37&41&45\\
54&60&66\\
95&106&117
\end{bmatrix}
\end{aligned}
\]
4.1.5 分块乘法
\[\left[\begin{array}{c|c}A_1&A_2\\\hline A_3&A_4\end{array}\right]\left[\begin{array}{c|c}B_1&B_2\\\hline B_3&B_4\end{array}\right]=\left[\begin{array}{c|c}A_1B_1+A_2B_3&A_1B_2+A_2B_4\\\hline A_3B_1+A_4B_3&A_3B_2+A_4B_4\end{array}\right]\]
在分块合适的情况下,可以简化运算。
4.2 逆(方阵)
4.2.1 概念
- 首先,并不是所有的方阵都有逆;而如果逆存在,则有 $A^{-1}A=I=AA^{-1}$。
- 对于方阵,左逆和右逆是相等的,但是对于非方阵(长方形矩阵),其左逆不等于右逆。
- 对于这些有逆的矩阵,我们称其为可逆的或非奇异的。
4.2.2 可逆的判断
我们先来看看奇异矩阵(不可逆的):\[A=\begin{bmatrix}1&2\\3&6\end{bmatrix}\],在后面将要学习的行列式中,会发现这个矩阵的行列式为 $0$。
- 观察这个方阵,我们如果用另一个矩阵乘 $A$,则得到的结果矩阵中的每一列应该都是 \[\begin{bmatrix}1\\2\end{bmatrix}\] 的倍数,所以我们不可能从 $AB$ 的乘积中得到单位矩阵 $I$。
- 另一种判定方法,如果存在非零向量 $x$,使得 $Ax=0$,则矩阵 $A$ 不可逆。
我们来用上面的矩阵为例:\[\begin{bmatrix}1&2\\3&6\end{bmatrix}\begin{bmatrix}3\\-1\end{bmatrix}=\begin{bmatrix}0\\0\end{bmatrix}\]。
- 证明:如果对于非零的 $x$ 仍有 $Ax=0$,而 $A$ 有逆 $A^{-1}$,则 $A^{-1}Ax=0$,即 $x=0$,与题设矛盾,得证。
现在来看看什么矩阵有逆,设 \[A=\begin{bmatrix}1&3\\2&7\end{bmatrix}\],我们来求 $A^{-1}$。\[\begin{bmatrix}1&3\\2&7\end{bmatrix}\begin{bmatrix}a&b\\c&d\end{bmatrix}=\begin{bmatrix}1&0\\0&1\end{bmatrix}\],使用列向量线性组合的思想,我们可以说 $A$ 乘以 $A^{-1}$ 的第 $j$ 列,能够得到 $I$ 的第 $j$ 列,这时我们会得到一个关于列的方程组。
4.2.3 逆矩阵的求法
接下来介绍(Gauss-Jordan)方法,该方法可以一次处理所有的方程:
-
这个方程组为\[\begin{cases}\begin{bmatrix}1&3\\2&7\end{bmatrix}\begin{bmatrix}a\\b\end{bmatrix}=\begin{bmatrix}1\\0\end{bmatrix}\\\\\begin{bmatrix}1&3\\2&7\end{bmatrix}\begin{bmatrix}c\\d\end{bmatrix}=\begin{bmatrix}0\\1\end{bmatrix}\end{cases}\],我们想要同时解这两个方程;
-
构造这样一个矩阵\[\left[\begin{array}{cc|cc}1&3&1&0\\2&7&0&1\end{array}\right]\],接下来用消元法将左侧变为单位矩阵;
- \[\left[\begin{array}{cc|cc}1&3&1&0\\2&7&0&1\end{array}\right]\xrightarrow{row_2-2row_1}\left[\begin{array}{cc|cc}1&3&1&0\\0&1&-2&1\end{array}\right]\xrightarrow{row_1-3row_2}\left[\begin{array}{cc|cc}1&0&7&-3\\0&1&-2&1\end{array}\right]\]
-
于是,我们就将矩阵从\[\left[\begin{array}{c|c}A&I\end{array}\right]\] 变为 \[\left[\begin{array}{c|c}I&A^{-1}\end{array}\right]\]
该方法的本质是使用消元矩阵 $E$,对 $A$ 进行操作,\[E\left[\begin{array}{c|c}A&I\end{array}\right]\],利用一步步消元有 $EA=I$,进而得到 \[\left[\begin{array}{c|c}I&E\end{array}\right]\],其实这个消元矩阵 $E$ 就是 $A^{-1}$,而 $I$ 只是负责记录消元的每一步操作,待消元完成,逆矩阵就自然出现了。