1.1快速排序
思想:
- 先取一个中间的任意值
x,将需要排序的序列划分为左右两个区间 - 以递增为例,使得左区间的数都满足
q[i]<=x右区间的数都满足q[i]>=x - 然后对左右两个区间分别排序最终得到递增序列
模板
int q[N]; //q[N]为需要排序的序列,需初始化为全局变量
void quick_sort(int q[],int l,int r){ //调用方法quick_sort(q,0,n-1) 其中n-1为末尾下标,即末边界
if(l>=r) return ; //若满足条件直接返回
int x=q[l+r>>1],i=l-1,j=r+1; //i,j为移动的两个指针
while(i<j){
do i++; while(q[i]<x); //i先移动,若q[i]<x则停止
do j--; while(q[j]>x); //j再移动,若q[j]>x则停止
if(i<j) swap(q[i],q[j]); //若两个指针未相遇,则交换两个值
}
quick_sort(q,l,j);
quick_sort(q,j+1,r); //递归处理区间
}
例题 785. 快速排序
描述
给定你一个长度为 n 的整数数列。
请你使用快速排序对这个数列按照从小到大进行排序。
并将排好序的数列按顺序输出。
输入格式
输入共两行,第一行包含整数 n。
第二行包含 n 个整数(所有整数均在 1∼109范围内),表示整个数列。
输出格式
输出共一行,包含 nn 个整数,表示排好序的数列。
数据范围
1≤n≤100000
输入样例:
5
3 1 2 4 5输出样例:
1 2 3 4 5代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int a[N];
void quick_sort(int q[],int l,int r){
if(l>=r) return ;
int x=q[l+r>>1],i=l-1,j=r+1;
while(i<j){
do i++; while(q[i]<x);
do j--; while(q[j]>x);
if(i<j) swap(q[i],q[j]);
}
quick_sort(q,l,j);
quick_sort(q,j+1,r);
}
int main(){
int n;
cin>>n;
for(int i=0;i<n;i++){
cin>>a[i];
}
quick_sort(a,0,n-1);
for(int i=0;i<n;i++){
cout<<a[i]<<" ";
}
return 0;
}1.2归并排序
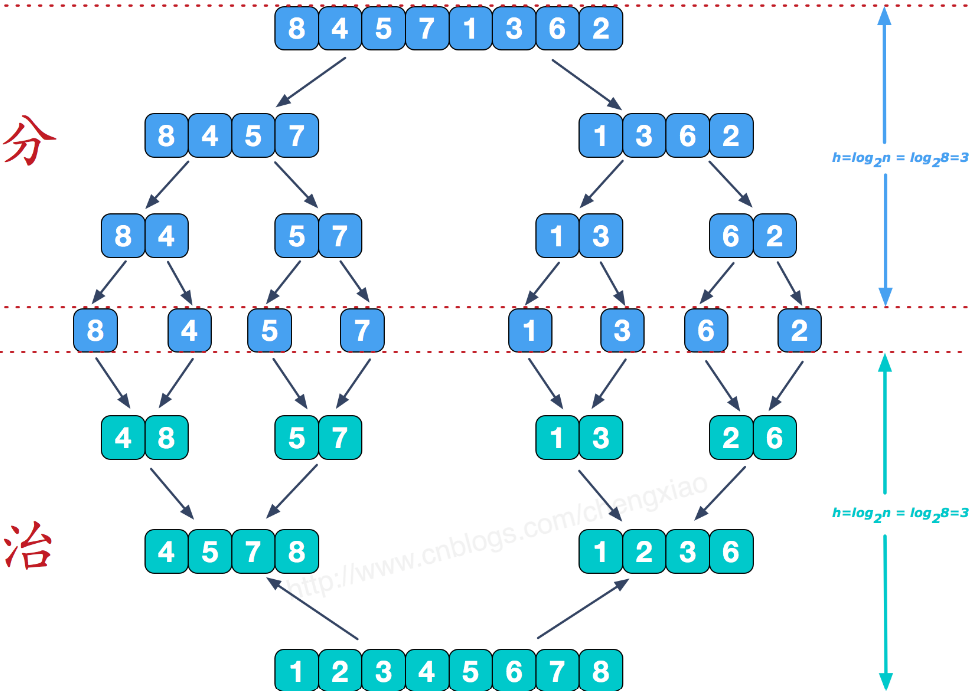
思想:——分治
- 先取需要排序的序列中点位置,将序列分为左右两个区间
- 递归对左右两个区间分别排序
- 开辟一个新空间,利用两个指针将两个序列的数存入
模板
int q[N],t[N]; //归并排序需要额外开辟一个新数组,用于存储答案
void merge_sort(int q[],int l,int r){ //调用方法merge_sort(q,0,n-1) 其中n-1为末尾下标,即末边界
if(l==r) return ;
int mid=l+r>>1; //取中间下标mid作为分界
merge_sort(q,l,mid); //递归排序左右两个区间
merge_sort(q,mid+1,r);
int k=0,i=l,j=mid+1;
while(i<=mid&&j<=r){ //归并过程
if(q[i]<=q[j]) t[k++]=q[i++];
else t[k++]=q[j++];
}
while(i<=mid) t[k++]=q[i++]; //若有剩下的进行扫尾
while(j<=r) t[k++]=q[j++];
for(int i=l,j=0;i<=r;i++,j++){ //更新答案
q[i]=t[j];
}
}
例题 788. 逆序对的数量
描述
给定一个长度为 n 的整数数列,请你计算数列中的逆序对的数量。
逆序对的定义如下:对于数列的第 i 个和第 j 个元素,如果满足 i<j 且 a[i]>a[j],则其为一个逆序对;否则不是。
输入格式
第一行包含整数 n,表示数列的长度。
第二行包含 n 个整数,表示整个数列。
输出格式
输出一个整数,表示逆序对的个数。
数据范围
1≤n≤100000,
数列中的元素的取值范围 [1,109]。
输入样例:
6
2 3 4 5 6 1输出样例:
5分析
- 判断逆序对数量,即在归并过程中利用
i和j两个指针判断 - 如果
q[i]>q[j],则之后的q[i]均大于q[j] - 即跟
q[i]组成逆序对的数量为mid-i+1
代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int a[N],t[N];
long long ans=0;
void merge_sort(int q[],int l,int r){
if(l==r) return ;
int mid=l+r>>1;
merge_sort(q,l,mid);
merge_sort(q,mid+1,r);
int k=0,i=l,j=mid+1;
while(i<=mid&&j<=r){
if(q[i]<=q[j]) t[k++]=q[i++];
else{
t[k++]=q[j++];
ans+=mid-i+1;
}
}
while(i<=mid) t[k++]=q[i++];
while(j<=r) t[k++]=q[j++];
for(int i=l,j=0;i<=r;i++,j++){
q[i]=t[j];
}
}
int main(){
int n;
cin>>n;
for(int i=0;i<n;i++){
cin>>a[i];
}
merge_sort(a,0,n-1);
cout<<ans;
return 0;
}1.3 二分
1.3.1 整数二分
思想
- 对于一个有序区间,要求二分的边界点使得左右区间分别满足某种性质
- 即对于
A点左边的区间和B点右边的区间满足某种性质,A和B可重合,也可只在其满足的性质区间内。
模板
bool check(int x){
//检查x是否满足某种性质,可写可不写,在判断时直接替换
}
//当需要二分的区间为红色区间,所求分界点为A时调用bsearch_1
int bsearch_1(int l,int r){ //l和r为边界
while(l<r){
int mid=l+r+1>>1; //mid下取整,若不补上+1,当l=r-1时,mid=l,若此时恰好check(mid)为true时会死循环
if(check(mid)) l=mid; //若为true则说明实际边界在mid右边,故更新左边界为mid
else r=midr-1; //否则实际边界在mid左边,且不包含mid
}
return l;
}
//当需要二分的区间为绿色区间,所求分界点为B时调用bsearch_2
int bsearch_2(int l,int r){
while(l<r){
inr mid=l+r>>1;
if(check(mid)) r=mid; //若为true则说明实际边界在mid左边,故更新右边界为mid
else l=mid+1; //否则实际边界在mid右边,且不包含mid
}
return l;
}例题 789. 数的范围
描述
给定一个按照升序排列的长度为 n 的整数数组,以及 q 个查询。
对于每个查询,返回一个元素 k 的起始位置和终止位置(位置从 0 开始计数)。
如果数组中不存在该元素,则返回 -1 -1。
输入格式
第一行包含整数 n 和 q,表示数组长度和询问个数。
第二行包含 n 个整数(均在 1∼10000 范围内),表示完整数组。
接下来 q 行,每行包含一个整数 k,表示一个询问元素。
输出格式
共 q 行,每行包含两个整数,表示所求元素的起始位置和终止位置。
如果数组中不存在该元素,则返回 -1 -1。
数据范围
1≤n≤100000
1≤q≤10000
1≤k≤10000
输入样例:
6 3
1 2 2 3 3 4
3
4
5输出样例:
3 4
5 5
-1 -1
代码
#include <bits/stdc++.h>
using namespace std;
int k,a[100010];
int bsearch_1(int l,int r){
while(l<r){
int mid=l+r+1>>1;
if(a[mid]<=k) l=mid;
else r=mid-1;
}
return l;
}
int bsearch_2(int l,int r){
while(l<r){
int mid=l+r>>1;
if(a[mid]>=k) r=mid;
else l=mid+1;
}
return l;
}
int main(){
int n,q;
cin>>n>>q;
for(int i=0;i<n;i++){
cin>>a[i];
}
while(q--){
cin>>k;
if(a[bsearch_1(0,n-1)]==k&&a[bsearch_2(0,n-1)]==k){
cout<<bsearch_2(0,n-1)<<" "<<bsearch_1(0,n-1)<<endl;
}
else cout<<"-1 -1"<<endl;
}
return 0;
}1.3.2 浮点数二分
模板
bool check(int x){
//检查x是否满足某种性质,可写可不写,在判断时直接替换
}
double bsearch_3(double l,double r){ //l和r为需要二分的区间
const double rep=1e-10; //区间精度
while(r-l>rep){
double mid=(l+r)/2;
if(check(mid)) r=mid; //根据题意更新区间
else l=mid; //根据题意更新区间
}
return l;
}例题 790. 数的三次方根
描述
给定一个浮点数 n,求它的三次方根。
输入格式
共一行,包含一个浮点数 n。
输出格式
共一行,包含一个浮点数,表示问题的解。
注意,结果保留 6 位小数。
数据范围
−10000≤n≤10000输入样例:
输入样例:
1000.00输出样例:
10.000000代码
#include <bits/stdc++.h>
using namespace std;
double n;
double bsearch_3(double l,double r){
const double rep=1e-10;
while(r-l>rep){
double mid=(l+r)/2;
if(pow(mid,3)>=n) r=mid;
else l=mid;
}
return l;
}
int main(){
cin>>n;
printf("%.6lf",bsearch_3(-10000,10000));
return 0;
}1.4 高精度
思想
- 先预处理读入的数据
- 利用
vector容器来模拟高精度运算过程
预处理
#include <bits/stdc++.h>
using namespace std;
vector<int> A,B; //用于存放两个大整数
vector<int> fx(vector<int> &A,vector<int> &B){ //定义运算函数
//模拟运算过程
}
int main(){
string a,b;
cin>>a>>b; //读入两个大整数
for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0'); //倒序存储大整数的每一位到A
for(int i=b.size()-1;i>=0;i--) B.push_back(b[i]-'0');
vector<int> C=fx(A,B); //调用运算函数
for(int i=C.size()-1;i>=0;i--) cout<<C[i]; //输出结果
return 0;
}1.4.1 高精度加法
模板
vector<int> add(vector<int> &A,vector<int> &B){
if(A.size()<B.size()) return add(B,A); //判断A和B的长度
int k=0; //定义进位,初始化为0
vector<int> C; //存储答案
for(int i=0;i<A.size();i++){ //遍历模拟
k+=A[i]; //进位加A本位
if(i<B.size()) k+=B[i]; //如果B未遍历完,则加上B本位
C.push_back(k%10); //存入答案
k/=10; //更新进位
}
if(k) C.push_back(k); //如果最后进位非零,则补上进位
return C;
}例题 791. 高精度加法
描述
给定两个正整数(不含前导 0),计算它们的和。
输入格式
共两行,每行包含一个整数。
输出格式
共一行,包含所求的和。
数据范围
1≤整数长度≤100000
输入样例:
12
23输出样例:
35代码
#include <bits/stdc++.h>
using namespace std;
vector<int> A,B;
vector<int> add(vector<int> &A, vector<int> &B){
if(A.size()<B.size()) return add(B,A);
int k=0;
vector<int> C;
for(int i=0;i<A.size();i++){
k+=A[i];
if(i<B.size()) k+=B[i];
C.push_back(k%10);
k/=10;
}
if(k) C.push_back(k);
return C;
}
int main(){
string a,b;
cin>>a>>b;
for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
for(int i=b.size()-1;i>=0;i--) B.push_back(b[i]-'0');
vector<int> C=add(A,B);
for(int i=C.size()-1;i>=0;i--) cout<<C[i];
return 0;
}1.4.2 高精度减法
- 在进行减法运算时,要考虑两个数的大小
模板
bool cmp(vector<int> &A,vector<int> &B){ //比较两个数大小
if(A.size()!=B.size()) return A.size()>B.size(); //当A和B长度不相等时,A>B返回true
else{
for(int i=A.size()-1;i>=0;i--){
if(A[i]!=B[i]) return A[i]>B[i]; //当从最高位开始遍历到不相等的数时,A[i]>B[i]返回true
}
}
return 1; //若遍历结束未返回,说明相等,返回true 若返回false,后续处理麻烦
}
vector<int> sub(vector<int> &A,vector<int> &B){
int k=0; //定义借位,初始化为0
vector<int> C; //存储答案
for(int i=0;i<A.size();i++){
int t=A[i]-k; //A本位减借位
if(i<B.size()) t-=B[i]; //如果B未遍历完,减B本位
if(t<0) t+=10,k=1; //若答案t<0,则t+10,且借位k更新为1
else k=0; //否则借位k更新为0
C.push_back(t%10); //存入答案
}
while(C.size()>1&&C.back()==0) C.pop_back(); //去除前导0
return C;
}例题 792. 高精度减法
描述
给定两个正整数(不含前导 0),计算它们的差,计算结果可能为负数。
输入格式
共两行,每行包含一个整数。
输出格式
共一行,包含所求的差。
数据范围
1≤整数长度≤105
输入样例:
32
11输出样例:
21代码
#include <bits/stdc++.h>
using namespace std;
vector<int> A,B;
bool cmp(vector<int> &A,vector<int> &B){
if(A.size()!=B.size()) return A.size()>B.size();
else{
for(int i=A.size()-1;i>=0;i--){
if(A[i]!=B[i]) return A[i]>B[i];
}
}
return 1;
}
vector<int> sub(vector<int> &A,vector<int> &B){
int k=0;
vector<int> C;
for(int i=0;i<A.size();i++){
int t=A[i]-k;
if(i<B.size()) t-=B[i];
if(t<0) t+=10,k=1;
else k=0;
C.push_back(t%10);
}
while(C.size()>1&&C.back()==0) C.pop_back();
return C;
}
int main(){
string a,b;
cin>>a>>b;
for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
for(int i=b.size()-1;i>=0;i--) B.push_back(b[i]-'0');
vector<int> C;
if(cmp(A,B)) C=sub(A,B); //当A>=B时,答案为0或正值
else C=sub(B,A),cout<<"-"; //当A<B时,答案为负值
for(int i=C.size()-1;i>=0;i--) cout<<C[i];
return 0;
}1.4.3 高精度乘法
- 一般为一个大整数乘以
A一个小整数b
模板
vector<int> mul(vector<int> &A,int b){
int k=0; //定义进位,初始化为0
vector<int> C; //存储答案
for(int i=0;i<A.size();i++){
k+=A[i]*b; //进位加A本位乘以b
C.push_back(k%10); //存入答案
k/=10; //更新进位
}
if(k) C.push_back(k); //如果最后进位非零,则补上进位
while(C.size()>1&&C.back()==0) C.pop_back(); //去除前导0
return C;
}例题 793. 高精度乘法
描述
给定两个非负整数(不含前导 0) A 和 B,请你计算 A×B 的值。
输入格式
共两行,第一行包含整数 A,第二行包含整数 B。
输出格式
共一行,包含 A×B 的值。
数据范围
1≤A的长度≤100000,
0≤B≤10000
输入样例:
2
3输出样例:
6代码
#include <bits/stdc++.h>
using namespace std;
vector<int> A;
vector<int> mul(vector<int> &A,int b){
int k=0;
vector<int> C;
for(int i=0;i<A.size();i++){
k+=A[i]*b;
C.push_back(k%10);
k/=10;
}
if(k) C.push_back(k);
while(C.size()>1&&C.back()==0) C.pop_back();
return C;
}
int main(){
string a;
int b;
cin>>a>>b;
for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
vector<int> C=mul(A,b);
for(int i=C.size()-1;i>=0;i--) cout<<C[i];
return 0;
}1.4.4 高精度除法
- 一般为一个大整数除以
A一个小整数b,求商和余数 - 进行除法运算时从最高位开始运算,但为保持一致性,仍倒序存储
A
模板
vector<int> div(vector<int> &A,int b,int &r){
vector<int> C; //存储答案
r=0; //初始化余数为0
for(int i=A.size()-1;i>=0;i--){ //从最高位开始遍历
int k=r*10+A[i]; //定义除数k为余数r*10加A本位
C.push_back(k/b); //存入答案
r=k%b; //更新余数
}
reverse(C.begin(),C.end()); //由于答案从最高位开始存入,故需翻转
while(C.size()>1&&C.back()==0) C.pop_back(); //去除前导0
return C;
}例题 794. 高精度除法
描述
给定两个非负整数(不含前导 0) A,B,请你计算 A/B 的商和余数。
输入格式
共两行,第一行包含整数 A,第二行包含整数 B。
输出格式
共两行,第一行输出所求的商,第二行输出所求余数。
数据范围
1≤A的长度≤100000,
1≤B≤10000,
B 一定不为 0
输入样例:
7
2输出样例:
3
1代码
#include <bits/stdc++.h>
using namespace std;
vector<int> A;
vector<int> div(vector<int> &A,int b,int &r){
vector<int> C;
r=0;
for(int i=A.size()-1;i>=0;i--){
int k=r*10+A[i];
C.push_back(k/b);
r=k%b;
}
reverse(C.begin(),C.end());
while(C.size()>1&&C.back()==0) C.pop_back();
return C;
}
int main(){
string a;
int b,r;
cin>>a>>b;
for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
vector<int> C=div(A,b,r);
for(int i=C.size()-1;i>=0;i--) cout<<C[i];
cout<<endl<<r;
return 0;
}1.5 前缀和与差分
1.5.1 一维前缀和与一位差分
思想
- 对于一个数组
a[N]和一个数组b[N],满足b[i] = a[0] + a[1] + a[2] +...+ a[i] - 则称
b[N]为a[N]的一维前缀和数组,称a[N]为b[N]的一维差分数组 - 一维前缀和与一维差分互为逆运算
模板
//给定含有n个元素的差分数组a[N],构造前缀和数组b[N]
for(int i=1;i<=n;i++){
b[i]=b[i-1]+a[i];
}
//给定含有n个元素的前缀和数组b[N],构造差分数组a[N]
for(int i=1;i>=n;i++){
a[i]=b[i]-b[i-1];
}应用及原理
- 对于一个数组,给定边界
l和r,可以构造其一维前缀和数组快速求出其区间内元素的
//给定一个数组a[N],构造其前缀和数组为b[N],查询l到r区间的元素和
b[r] = a[0] + a[1] + ... + a[l-1] + a[l] + a[l+1] + ... + a[r-1] + a[r] ;
b[l-1] = a[0] + a[1] + ... + a[l-1] ;
b[r] - b[l-1] = a[l] + a[l+1] + ... + a[r-1] + a[r] ;- 对于一个数组,给定边界
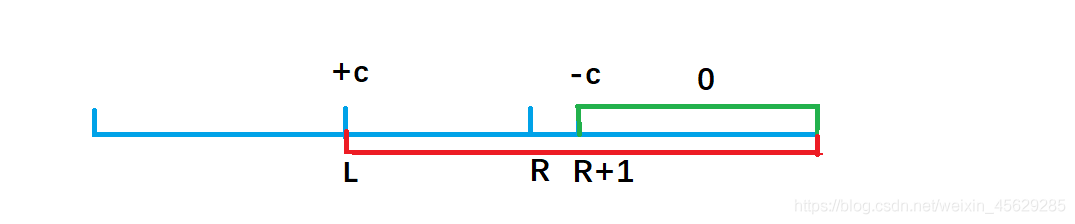
l和r,要求其区间的所有元素加或减一个常数c,通过构造该数组的差分数组来快速完成操作
//给定一个数组a[N],构造其差分数组为b[N],现使得a[N]中l到r区间的所有元素加上c,求操作后的a[N]数组
b[l]+=c; //通过前缀和运算,a数组变成 a[l] + c + a[l+1] + c + ... + a[n] + c
b[r+1]-=c; //通过前缀和运算,a数组变成 a[r+1] - c + a[r+2] - c + ... + a[n] - c
for(int i=1;i<=n;i++){
a[i]=a[i-1]+b[i]; //得到操作后的数组a[N]
}
例题 795. 前缀和
描述
输入一个长度为 n 的整数序列。
接下来再输入 m 个询问,每个询问输入一对 l,r。
对于每个询问,输出原序列中从第 l 个数到第 r 个数的和。
输入格式
第一行包含两个整数 n 和 m。
第二行包含 n 个整数,表示整数数列。
接下来 m 行,每行包含两个整数 l 和 r,表示一个询问的区间范围。
输出格式
共 m 行,每行输出一个询问的结果。
数据范围
1≤l≤r≤n,
1≤n,m≤100000,
−1000≤数列中元素的值≤1000
输入样例:
5 3
2 1 3 6 4
1 2
1 3
2 4输出样例:
3
6
10代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int a[N],b[N];
int main(){
int n,q;
scanf("%d%d",&n,&q);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
b[i]=b[i-1]+a[i];
}
while(q--){
int l,r;
scanf("%d%d",&l,&r);
printf("%d\n",b[r]-b[l-1]);
}
return 0;
}例题 797. 差分
描述
输入一个长度为 n 的整数序列。
接下来输入 m 个操作,每个操作包含三个整数 l,r,c,表示将序列中 [l,r] 之间的每个数加上 c。
请你输出进行完所有操作后的序列。
输入格式
第一行包含两个整数 n 和 m。
第二行包含 n 个整数,表示整数序列。
接下来 m 行,每行包含三个整数 l,r,c,表示一个操作。
输出格式
共一行,包含 n 个整数,表示最终序列。
数据范围
1≤n,m≤100000,
1≤l≤r≤n,
−1000≤c≤1000,
−1000≤整数序列中元素的值≤1000
输入样例:
6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1输出样例:
3 4 5 3 4 2代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int a[N],b[N];
int main(){
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
b[i]=a[i]-a[i-1];
}
while(m--){
int l,r,c;
scanf("%d%d%d",&l,&r,&c);
b[l]+=c;
b[r+1]-=c;
}
for(int i=1;i<=n;i++){
a[i]=a[i-1]+b[i];
printf("%d ",a[i]);
}
return 0;
}1.5.2 二维前缀和与二维差分
思想
-
对于一个二维矩阵
a[N][N]和一个二维矩阵b[N][N],满足b[i][j]为以a[1][1]为左上角到以a[i][j]为右下角的矩阵中所有元素的和,即b[i][j] = a[1][1] + a[1][2] + ... + a[i][j-1] + a[i][j] -
则称
b[N][N]为a[N][N]的二维前缀和数组,称a[N][N]为b[N][N]的二维差分数组 -
二维前缀和与二维差分互为逆运算
模板
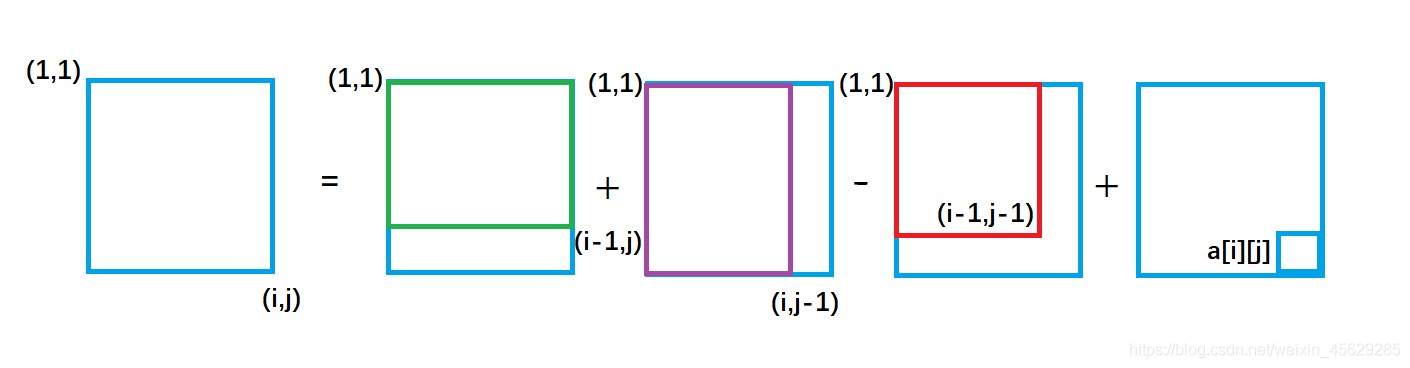
//给定含有n行m列的二维数组a[N][N],构造其二维前缀和数组b[N][N]
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
b[i][j]=a[i][j]+b[i-1][j]+b[i][j-1]-b[i-1][j-1];
}
}
//给定含有n行m列的二维数组b[N][N],构造其二维差分数组a[N][N]
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
a[i][j]=b[i][j]-b[i-1][j]-b[i][j-1]+a[i-1][j-1];
}
}应用及原理
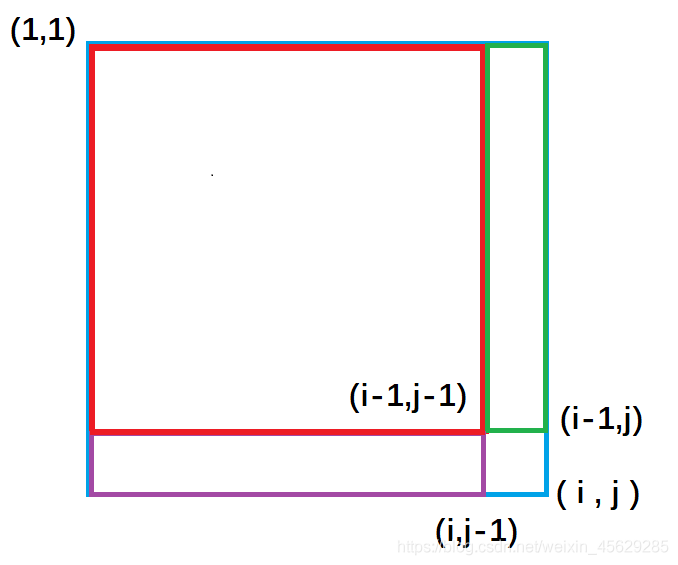
- 对于一个二维数组,给定
(x1,y1)和(x2,y2),求以(x1,y1)为左上角到以(x2,y2)为右下角的子矩阵中所有元素的和
/* 给定一个二维数组a[N][N],构造其二维前缀和数组为b[N][N],给定坐标(x1,y1)和(x2,y2),求以(x1,y1)为左上角到以(x2,y2)为右下角的子矩阵中所有元素的和 */
long long sum=0;
sum = b[x2][y2] - b[x1 - 1][y2] - b[x2][y1 - 1] + b[x1 - 1][y1 - 1];
- 对于一个二维数组,给定
(x1,y1)和(x2,y2),对以(x1,y1)为左上角到以(x2,y2)为右下角的子矩阵中的所有元素加或减一个常数c,可通过构造该二维数组的二维差分数组来快速完成操作
/*给定一个二维数组a[N][N],构造其二维差分数组为b[N][N],给定坐标(x1,y1)和(x2,y2),对以(x1,y1)为左上角到以(x2,y2)为右下角的子矩阵中所有元素加或减一个常数c,求操作后的数组a[N][N] */
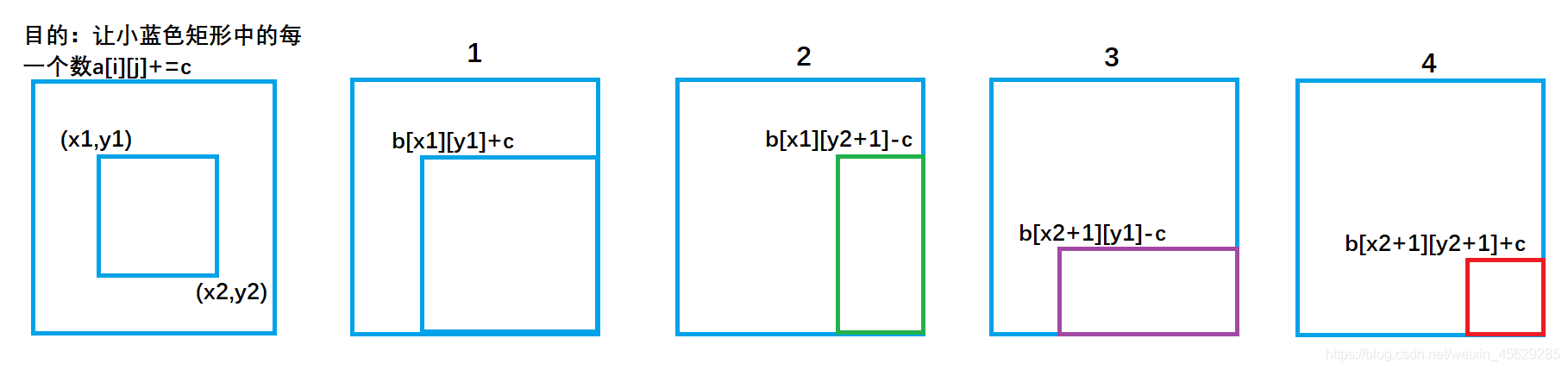
b[x1][y1]+=c;
b[x1][y2+1]-=c;
b[x2+1][y1]-=c;
b[x2+1][y2+1]+=c
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
a[i][j]=b[i][j]+b[i-1][j]+b[i][j-1]-b[i-1][j-1]; //得到操作后的数组a[N][N]
}
}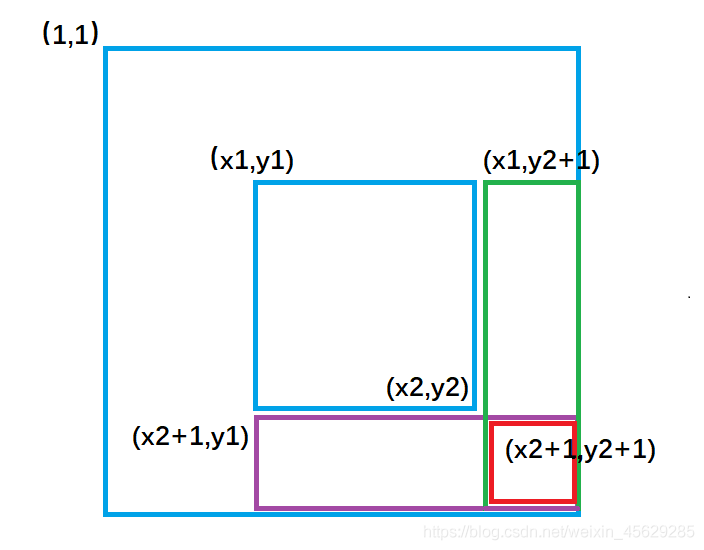
b[x1][y1]+=c 对应图1 ,让整个a数组中蓝色矩形面积的元素都加上了c。
b[x1][y2+1]-=c 对应图2 ,让整个a数组中绿色矩形面积的元素再减去c,使其内元素不发生改变。
b[x2+1][y1]-=c 对应图3 ,让整个a数组中紫色矩形面积的元素再减去c,使其内元素不发生改变。
b[x2+1][y2+1]+=c 对应图4,,让整个a数组中红色矩形面积的元素再加上c,红色内的相当于被减了两次,再加上一次c,才能使其恢复。
例题 796. 子矩阵的和
描述
输入一个 n 行 m 列的整数矩阵,再输入 q 个询问,每个询问包含四个整数 x1,y1,x2,y2,表示一个子矩阵的左上角坐标和右下角坐标。
对于每个询问输出子矩阵中所有数的和。
输入格式
第一行包含三个整数 n,m,q。
接下来 n 行,每行包含 m 个整数,表示整数矩阵。
接下来 q 行,每行包含四个整数 x1,y1,x2,y2,表示一组询问。
输出格式
共 q 行,每行输出一个询问的结果。
数据范围
1≤n,m≤1000,
1≤q≤200000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤矩阵内元素的值≤1000
输入样例:
3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4输出样例:
17
27
21代码
#include <bits/stdc++.h>
using namespace std;
const int N=1010;
int a[N][N],b[N][N];
int main(){
int n,m,q;
scanf("%d%d%d",&n,&m,&q);
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
scanf("%d",&a[i][j]);
b[i][j]=a[i][j]+b[i-1][j]+b[i][j-1]-b[i-1][j-1];
}
}
while(q--){
int x1,y1,x2,y2;
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
printf("%d\n",b[x2][y2]-b[x1-1][y2]-b[x2][y1-1]+b[x1-1][y1-1]);
}
return 0;
}例题 798. 差分矩阵
描述
输入一个 n 行 m 列的整数矩阵,再输入 q 个操作,每个操作包含五个整数 x1,y1,x2,y2,c,其中 (x1,y1) 和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。
每个操作都要将选中的子矩阵中的每个元素的值加上 c。
请你将进行完所有操作后的矩阵输出。
输入格式
第一行包含整数 n,m,q。
接下来 n 行,每行包含 m 个整数,表示整数矩阵。
接下来 q 行,每行包含 5 个整数 x1,y1,x2,y2,c,表示一个操作。
输出格式
共 n 行,每行 m 个整数,表示所有操作进行完毕后的最终矩阵。
数据范围
1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000
输入样例:
3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1输出样例:
2 3 4 1
4 3 4 1
2 2 2 2代码
#include <bits/stdc++.h>
using namespace std;
const int N=1010;
int a[N][N],b[N][N];
int main(){
int n,m,q;
scanf("%d%d%d",&n,&m,&q);
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
scanf("%d",&a[i][j]);
b[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1];
}
}
while(q--){
int x1,y1,x2,y2,c;
scanf("%d%d%d%d%d",&x1,&y1,&x2,&y2,&c);
b[x1][y1]+=c;
b[x1][y2+1]-=c;
b[x2+1][y1]-=c;
b[x2+1][y2+1]+=c;
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
a[i][j]=b[i][j]+a[i-1][j]+a[i][j-1]-a[i-1][j-1];
printf("%d ",a[i][j]);
}
puts("");
}
return 0;
}1.6 双指针算法
思想
-
将
O(n^2)的朴素算法优化到O(n) -
优化方法可以先朴素求解,然后找到两个指针的单调关系进行优化
模板
//常用模板
for(int i=0,j=0;i<n;i++){
while(check(i,j)) j++;
//题目逻辑
}
//对于一个序列,用两个指针维护一段区间
//对于两个序列,维护某种次序,比如归并排序中合并两个有序序列的操作例题 799. 最长连续不重复子序列
描述
给定一个长度为 n 的整数序列,请找出最长的不包含重复的数的连续区间,输出它的长度。
输入格式
第一行包含整数 n。
第二行包含 n 个整数(均在 0∼105 范围内),表示整数序列。
输出格式
共一行,包含一个整数,表示最长的不包含重复的数的连续区间的长度。
数据范围
1≤n≤105
输入样例:
5
1 2 2 3 5输出样例:
3代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int a[N],b[N];
int main(){
int n,ans=0;
scanf("%d",&n);
for(int i=0;i<n;i++) scanf("%d",&a[i]);
for(int i=0,j=0;i<n;i++){
b[a[i]]++; //先使i指针向右移动,并记录目前区间里元素的个数
while(b[a[i]]>1){ //出现重复数字则开始将j指针向右移动,直到区间元素唯一
b[a[j]]--;
j++;
}
ans=max(ans,i-j+1); //更新区间长度
}
printf("%d",ans);
return 0;
}例题
描述
给定两个升序排序的有序数组 A 和 B,以及一个目标值 x。
数组下标从 0 开始。
请你求出满足 A[i]+B[j]=x 的数对 (i,j)。
数据保证有唯一解。
输入格式
第一行包含三个整数 n,m,x,分别表示 A 的长度,B 的长度以及目标值 x。
第二行包含 n 个整数,表示数组 A。
第三行包含 m 个整数,表示数组 B。
输出格式
共一行,包含两个整数 i 和 j。
数据范围
数组长度不超过 105。
同一数组内元素各不相同。
1≤数组元素≤109
输入样例:
4 5 6
1 2 4 7
3 4 6 8 9输出样例:
1 1代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int a[N],b[N];
int main(){
int n,m,k;
scanf("%d%d%d",&n,&m,&k);
for(int i=0;i<n;i++) scanf("%d",&a[i]);
for(int i=0;i<m;i++) scanf("%d",&b[i]);
for(int i=0,j=m-1;i<n;i++){
while(a[i]+b[j]>k) j--;
if(a[i]+b[j]==k){
printf("%d %d",i,j);
return 0;
}
}
return 0;
}例题 2816. 判断子序列
描述
给定一个长度为 n 的整数序列 a1,a2,…,an 以及一个长度为 m 的整数序列 b1,b2,…,bm。
请你判断 a 序列是否为 b 序列的子序列。
子序列指序列的一部分项按原有次序排列而得的序列,例如序列 {a1,a3,a5} 是序列 {a1,a2,a3,a4,a5} 的一个子序列。
输入格式
第一行包含两个整数 n,m。
第二行包含 n 个整数,表示 a1,a2,…,an。
第三行包含 m 个整数,表示 b1,b2,…,bm。
输出格式
如果 a 序列是 b 序列的子序列,输出一行 Yes。
否则,输出 No。
数据范围
1≤n≤m≤105,
−109≤ai,bi≤109
输入样例:
3 5
1 3 5
1 2 3 4 5输出样例:
Yes代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int a[N],b[N];
int main(){
int n,m;
scanf("%d%d",&n,&m);
for(int i=0;i<n;i++) scanf("%d",&a[i]);
for(int i=0;i<m;i++) scanf("%d",&b[i]);
for(int i=0,j=0;j<m;j++){
if(a[i]==b[j]) i++;
if(i==n){
printf("Yes");
return 0;
}
}
printf("No");
return 0;
} 1.7 位运算
运算符及运算规则
& //与运算
0 & 0 = 0 ;
0 & 1 = 0 ;
1 & 0 = 0 ;
1 & 1 = 1 ;
| //或运算
0 | 0 = 0 ;
0 | 1 = 1 ;
1 | 0 = 1 ;
1 | 1 = 1 ;
~ //取反运算
~ 0 = 1 ;
~ 1 = 0 ;
^ //异或运算
0 ^ 0 = 0 ;
0 ^ 1 = 1 ;
1 ^ 0 = 1 ;
1 ^ 1 = 0 ;
>> //右移运算
n >> k //表示 n / 2^k
<< //左移运算
n << k //表示 n * 2*k
常用模板
//求x的第k位数字
x >> k & 1 ;
//求x的最后一位1
x & -x ;例题 二进制中1的个数
描述
给定一个长度为 n 的数列,请你求出数列中每个数的二进制表示中 1 的个数。
输入格式
第一行包含整数 n。
第二行包含 n 个整数,表示整个数列。
输出格式
共一行,包含 n 个整数,其中的第 i 个数表示数列中的第 i 个数的二进制表示中 1 的个数。
数据范围
1≤n≤100000,
0≤数列中元素的值≤109
输入样例:
5
1 2 3 4 5输出样例:
1 1 2 1 2代码
#include <bits/stdc++.h>
using namespace std;
void solve(){
int n; cin >> n;
int cnt = 0;
while(n){
cnt += n & 1;
n >>= 1;
}
cout << cnt << ' ';
}
int main(){
int _; cin >> _;
while(_ --) solve();
return 0;
}1.8 离散化
思想
- 对于值域很大,数据量很小的情况下,将值作为映射来节省空间
- 将所有数据进行排序后去重
- 利用二分得到原数值所对应的映射下标
模板
vector<int> nums; //预先存入要映射的值
sort(nums.begin(),nums.end()); //对数据进行排序
erase(unique(nums.begin(),nums.end()),nums.end()); //去重并删除重复的元素
int find(int x){ //二分查找
int l=0,r=nums.size()-1;
while(l<r){
int mid=l+r>>1;
if(nums[mid]>=x) r=mid;
else l=mid+1;
}
return l; //返回映射的下标
}例题 802.区间和
描述
假定有一个无限长的数轴,数轴上每个坐标上的数都是 0。
现在,我们首先进行 n 次操作,每次操作将某一位置 x 上的数加 c。
接下来,进行 m 次询问,每个询问包含两个整数 l 和 r,你需要求出在区间 [l,r] 之间的所有数的和。
输入格式
第一行包含两个整数 n 和 m。
接下来 n 行,每行包含两个整数 x 和 c。
再接下来 m 行,每行包含两个整数 l 和 r。
输出格式
共 m 行,每行输出一个询问中所求的区间内数字和。
数据范围
−109≤x≤109,
1≤n,m≤105,
−109≤l≤r≤109,
−10000≤c≤10000
输入样例:
3 3
1 2
3 6
7 5
1 3
4 6
7 8输出样例:
8
0
5代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int a[N],b[N]; //a[N]用于初始化加入操作,b[N]用于初始化前缀和
vector<int> nums; //用于存放需要映射的数
vector<pair<int,int>> add,q; //存放加入操作和询问操作
int find(int x){ //处理映射
int l=0,r=nums.size()-1;
while(l<r){
int mid=l+r>>1;
if(nums[mid]>=x) r=mid;
else l=mid+1;
}
return l+1; //由于前缀和从i=1开始,返回下标l+1
}
int main(){
int n,m;
cin>>n>>m;
for(int i=0;i<n;i++){
int x,c;
cin>>x>>c;
add.push_back({x,c}); //记录加入操作的下标x和加入的数c
nums.push_back(x); //将下标x存入处理映射的数组
}
for(int i=0;i<m;i++){
int l,r;
cin>>l>>r;
q.push_back({l,r}); //记录询问操作的两个边界
nums.push_back(l); //将边界下标存入处理映射的数组
nums.push_back(r);
}
sort(nums.begin(),nums.end()); //排序需要处理映射数组里的元素
nums.erase(unique(nums.begin(),nums.end()),nums.end()); //去掉重复元素
for(int i=0;i<add.size();i++){
a[find(add[i].first)]+=add[i].second; //进行处理映射的加入操作,
}
for(int i=1;i<=nums.size();i++) b[i]=b[i-1]+a[i]; //初始化前缀和数组
for(int i=0;i<q.size();i++){
cout<<b[find(q[i].second)]-b[find(q[i].first)-1]<<endl; //输出询问
}
return 0;
}离散化排序质数
例题 素数的排位
描述
小明在研究素数,已知素数序列为2、3、5、7、……,即第一个素数是2,第二个是3,……。他为搞清一些素数究竟在素数集合中排名老几,伤透了脑筋。还是请你帮他编个程序搞定吧,否则,他慢腾腾慢腾腾地数,数到什么时候去?
输入格式
多实例测试,每次输入为一个正整数N(1≤N≤1000000)
输出格式
运行结果每个数占1行,结果中的每个数是输入的正整数在素数集合中的排位。如果输入的不是素数(这太有可能了),那就输出一个0表示。
输入样例
2
6
4
5
13输出样例
1
0
0
3
6代码
#include <bits/stdc++.h>
using namespace std;
//欧拉筛筛选一定范围的质数,并存入数组
const int maxn=1e6+10; //筛选的质数范围
vector<bool>iscut(maxn + 1); //筛选标记,true-被筛掉,false-未筛除
vector<int>prime; //存储素数的容器
void Primes(int n){
for(int i=2;i<=n;i++)
{
if(!iscut[i]) //iscut[i]=false,即i未被筛掉,加入素数
prime.push_back(i);
for(int j=0;j<prime.size();j++)
{
if(i*prime[j]>n) //防越界
break;
iscut[i*prime[j]]=true; //把i的质数倍筛除
if(i%prime[j]==0) //*判断最小质因数,防止重复筛除
break;
}
}
}
int main(){
Primes(maxn); //初始化质数表
int n;
while(cin>>n){
int l=0,r=prime.size()-1; //二分查找该数是否存在于质数表中
while(l<r){
int mid=l+r>>1;
if(prime[mid]>n) r=mid;
else l=mid+1;
}
if(prime[l-1]==n) cout<<l<<endl;
else cout<<0<<endl;
}
return 0;
}
1.9 区间合并
思想
- 目的合并有交集的区间,对于给定的区间端点,对左端点进行排序
- 维护当前区间,当下一个区间左端点大于等于当前区间左端点时,只需判断下一个区间的右端点,并更新区间
- 如果下一个区间的左端点大于当前维护区间的右端点,则更新区间为该区间
例题 803.区间合并
描述
给定 n 个区间 [li,ri],要求合并所有有交集的区间。
注意如果在端点处相交,也算有交集。
输出合并完成后的区间个数。
例如:[1,3] 和 [2,6] 可以合并为一个区间 [1,6]。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含两个整数 l 和 r。
输出格式
共一行,包含一个整数,表示合并区间完成后的区间个数。
数据范围
1≤n≤100000,
−109≤li≤ri≤109
输入样例:
5
1 2
2 4
5 6
7 8
7 9输出样例:
3代码
#include <bits/stdc++.h>
using namespace std;
vector<pair<int,int>> a; //用于存放区间两个边界
long long ans=1; //初始化答案
bool cmp(pair<int,int> &p1,pair<int,int> &p2){ //重载比较函数
return p1.first<p2.first;
}
int main(){
int n,ll,rr;
cin>>n;
for(int i=0;i<n;i++){
int l,r;
cin>>l>>r;
a.push_back({l,r}); //存入边界
}
sort(a.begin(),a.end(),cmp); //对左端点排序
ll=a[0].first,rr=a[0].second; //初始化维护区间的左右端点
for(int i=1;i<a.size();i++){
if(a[i].first<=rr) rr=max(rr,a[i].second); //若下一个区间左端点小于等于当前区间右端点,则更新右端点
else{ //否则更新区间,ans++
ll=a[i].first;
rr=a[i].second;
ans++;
}
}
cout<<ans;
return 0;
}
评论
Deprecated: preg_replace(): Passing null to parameter #3 ($subject) of type array|string is deprecated in /var/www/html/wp-content/themes/argon/functions.php on line 1748