AC 自动机详解
liyusendesu
|
ALGORITHM,Intermediate Algorithm
|
|
913
|
0

2415 字
|
24 分钟
本文最后更新于 692 天前，其中的信息可能已经有所发展或是发生改变。

前置知识

字典树 Trie

Trie 是一种能够快速插入和查询字符串的多叉树结构。节点的编号各不相同，根节点编号为0，其他节点用来标识路径还可以标记单词插入的次数。边表示字符。

支持操作

Trie 维护字符串的集合，支持两种操作：

  • 向集合中插入一个字符串：void insert(char *s)
  • 在集合中查询一个字符串：int query(char *s)

建字典树

  • 儿子数组 ch[p][j] 存储从节点 p 沿着 j 这条边走到的子节点。
    • 边为 26 个小写字母 a ~ z 对应的映射值 0 ~ 25。
    • 每个节点最多可以有 26 个分叉。
  • 计数数组 cnt[p] 存储以节点 p 结尾的单词的插入次数。
  • 节点编号 idx 用来给节点编号。

实现思想

  • 空 Trie 仅有一个根节点，编号为 0。
  • 从根结点开始插，枚举字符串的每个字符：
    • 如果有儿子，则 p 指针走到儿子；
    • 如果没儿子，则先创建儿子，p 指针再走到儿子。
  • 在单词结束点记录插入次数。
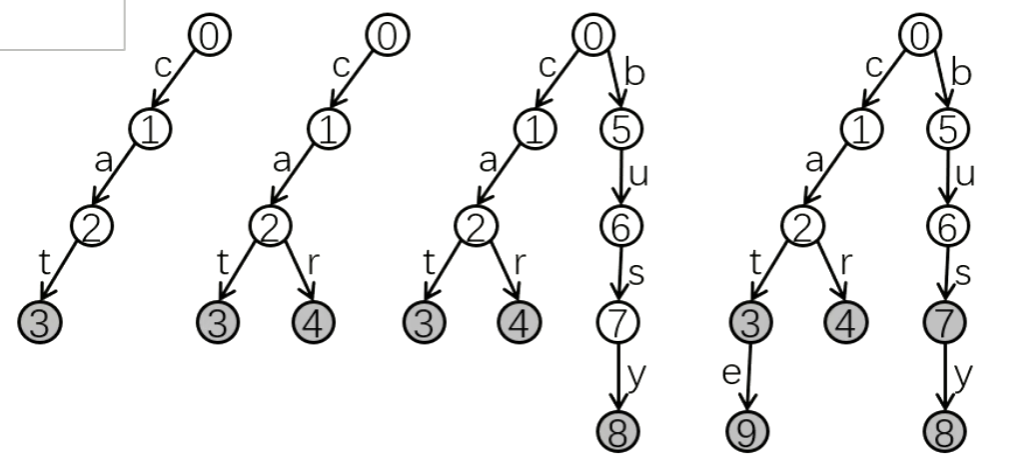
  • 例如：依次插入"cat", "car", "busy", "cate", "bus", "car"：

代码实现

const int N = 1e6 + 3;

int n;
string s;
int ch[N][27], cnt[N], idx;

void insert(string s){
    int p = 0;
    for(int i = 0; i < s.size(); i ++){
        int j = s[i] - 'a';  //字母的映射值
        if(!ch[p][j]) ch[p][j] = ++ idx;
        p = ch[p][j];
    }
    cnt[p] ++;  //插入次数
}

int query(string s){
    int p = 0;
    for(int i = 0; i < s.size(); i ++){
        int j = s[i] - 'a';
        if(!ch[p][j]) return 0;
        p = ch[p][j];
    }
    return cnt[p];
}

例题

Trie字符串统计

Original Link

维护一个字符串集合，支持两种操作：

  1. I x 向集合中插入一个字符串 $x$；
  2. Q x 询问一个字符串在集合中出现了多少次。

共有 $N$ 个操作，所有输入的字符串总长度不超过 $10^5$，字符串仅包含小写英文字母。

输入格式

第一行包含整数 $N$，表示操作数。

接下来 $N$ 行，每行包含一个操作指令，指令为 I x 或 Q x 中的一种。

输出格式

对于每个询问指令 Q x，都要输出一个整数作为结果，表示 $x$ 在集合中出现的次数。

每个结果占一行。

数据范围

$1≤N≤2\times 10^4 $

输入样例：

5
I abc
Q abc
Q ab
I ab
Q ab

输出样例：

1
0
1

代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 1e6 + 3;

int n;
string s;
int ch[N][27], cnt[N], idx;

void insert(string s){
    int p = 0;
    for(int i = 0; i < s.size(); i ++){
        int j = s[i] - 'a';  //字母的映射值
        if(!ch[p][j]) ch[p][j] = ++ idx;
        p = ch[p][j];
    }
    cnt[p] ++;  //插入次数
}

int query(string s){
    int p = 0;
    for(int i = 0; i < s.size(); i ++){
        int j = s[i] - 'a';
        if(!ch[p][j]) return 0;
        p = ch[p][j];
    }
    return cnt[p];
}

void solve(){
    int n; cin >> n;
    while(n --){
        string op; cin >> op >> s;
        if(op == "I") insert(s);
        else cout << query(s) << endl;
    }
}

int main(){
    solve();
    return 0;
}

最大异或对

Original Link

在给定的 $N$ 个整数 $A_1，A_2……A_N$ 中选出两个进行 $xor$（异或）运算，得到的结果最大是多少？

输入格式

第一行输入一个整数 $N$。

第二行输入 $N$ 个整数 $A_1，A_2……A_N$。

输出格式

输出一个整数表示答案。

数据范围

$1\le N \lt 10^5, 0\le A_i\le 2^{31}$

输入样例：

3
1 2 3

输出样例：

3

思想：

  • 异或运算即对数的二进制位进行运算，则先将 $N$ 个整数均转化为二进制数表示。
  • 二进制是 01 构成的串，构造 Tire 树，在树枝上进行异或运算。
  • 用 Trie 存整数，由整数的二进制位构造的 Trie，是一颗二叉树，深度为 31 层。

本质上：

  • 用 Trie 存单词，由 26 个小写字母构造的 Trie，是一颗26 叉树，深度为最长单词的长度。
  • 用 Trie 存整数，由整数的十进制位构造的 Trie，是一颗 10 叉树，深度为 10 层。

代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 1e6 + 3;

int n;
int a[N];  //存数
int ch[N * 31][3], cnt[N], idx;

void insert(int x){
    int p = 0;
    for(int i = 30; i >= 0; i --){
        int j = x >> i & 1;  //取出第 i 位
        if(!ch[p][j]) ch[p][j] = ++ idx;
        p = ch[p][j];
    }
}

int query(int x){
    int p = 0, res = 0;
    for(int i = 30; i >= 0; i --){
        int j = x >> i & 1;  //取出第 i 位
        if(ch[p][!j]){
            res += 1 << i;  //累加位权
            p = ch[p][!j];
        }
        else p = ch[p][j];
    }
    return res;
}

void solve(){
    int ans = 0;
    cin >> n;
    for(int i = 0; i < n; i ++) cin >> a[i], insert(a[i]);
    for(int i = 0; i < n; i ++) ans = max(ans, query(a[i]));
    cout << ans << endl;
}

int main(){
    solve();
    return 0;
}

AC自动机

基础概念

自动机是一个对信号序列进行判定的数学模型。

AC 自动机顾名思义就是 自动AC的机器，可以帮助你将难题直接Accept掉。

AC 自动机全称为 （Aho-Corasick automaton），该算法在 1975 年产生于贝尔实验室，是著名的多模匹配算法。所谓多模匹配算法，最常见的例子是给出 n 个单词，再给出一段包含 m 个字符的文章，让你找出有多少个单词在文章里出现过。

AC 自动机是 以 Trie 的结构为基础，结合 KMP 的思想 建立的。

实现思想

简单来说，建立一个 AC 自动机有两个必要结构：

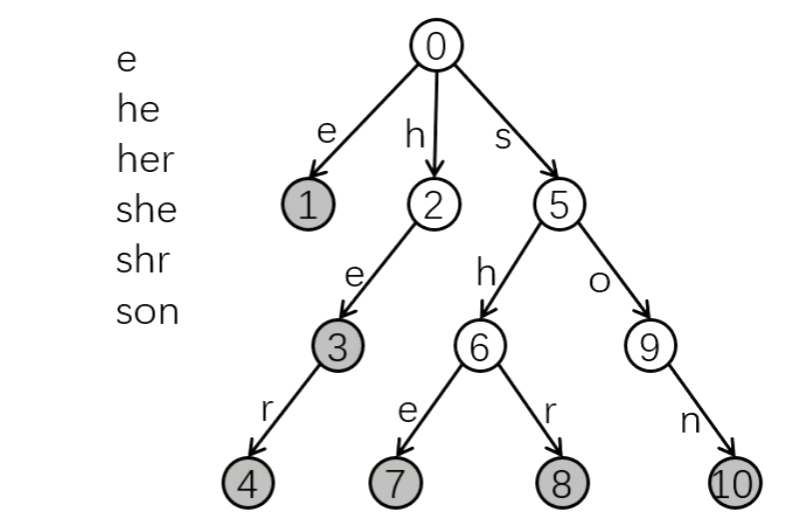
  • 基础的 Trie 结构：
    • 先用 n 个模式串构造一颗 Trie。
    • Trie 中的一个节点表示一个从根到当前节点的字符串，其中，根节点表示空串。
    • 如果节点是个模式串，则打个标记。
  • KMP 的思想：
    • 对 Trie 上所有的结点构造失配指针。
    • 即在 Trie 上构建两类边：回跳边和转移边。

最后就可以利用它扫描主串进行多模式匹配。

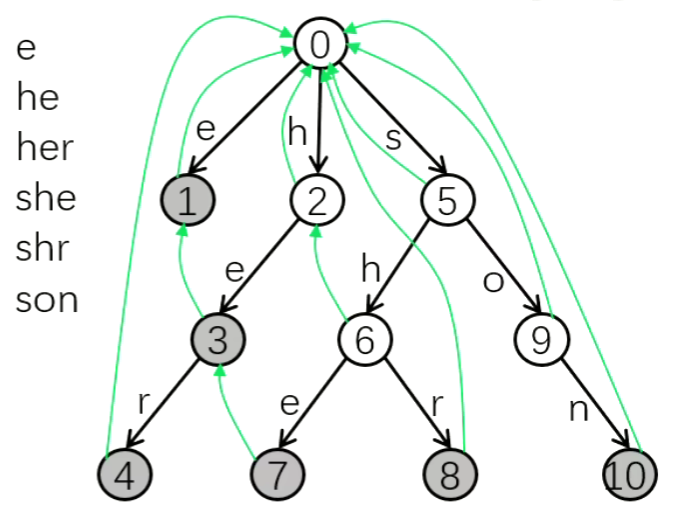
节点 $⑤$ 表示 "s"，节点 $⑥$ 表示 "sh"，节点 $⑦$ 表示 "she"。

具体地，对于构建两类边：

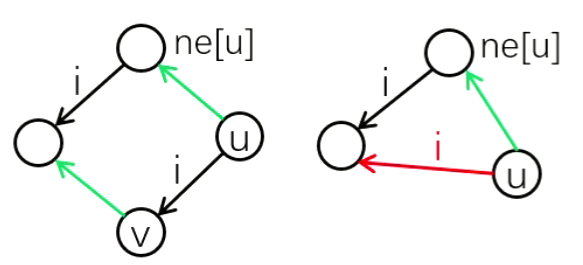
  • 回跳边：

    • ne[v] 存节点 v 的回跳边的终点。ne[7] = 3
    • 回跳边指向父节点的回跳边所指节点的儿子。
    • 四个点（v，u，ne[u]，ch[][]）构成四边形。
    • 回跳边所指节点一定是当前节点的最长后缀。

  • 转移边：

    • ch[u][i] 存节点 u 的树边的终点。ch[6][e] = 7。

    • ch[u][i] 存节点 u 的树边的终点。ch[6][e] = 7。

    • ch[u][i] 存节点 u 的转移边的终点。ch[7][r] = 4

    • 转移边指向当前节点的回跳边所指节点的儿子。

    • 三个点（u，ne[u]，ch[][]）构成三角形。

    • 转移边所指节点一定是当前节点的最短路。

  • 构造 AC 自动机：

    • 初始化，把根节点的儿子们入队。
    • 只要队不空，节点 u 出队，枚举 u 的 26 个儿子：
    • 若儿子存在，则爹帮儿子建回跳边，并把儿子入队。
    • 若儿子不存在，则爹自建转移边。

如图建立 AC 自动机的回跳边，转移边同理。

  • 查找单词出现次数：
    • 扫描主串，依次取出字符 s[k]
    • ⅰ 指针走主串对应的节点，沿着树边或转移边走且保证不回退。
    • j 指针沿着回跳边搜索模式串，每次从当前节点走到根节点，把当前节点中的所有后缀模式串遍历完，保证不漏解。
    • 扫描完主串，返回答案。

代码实现

const int N = 5e5 + 3;

int n;
string s;
int ch[N][26], cnt[N], idx;
int ne[N];

void insert(string s){  //键 Tire 树
    int p = 0;
    for(int i = 0; i < s.size(); i ++){
        int j = s[i] - 'a';
        if(!ch[p][j]) ch[p][j] = ++ idx;
        p = ch[p][j];
    }
    cnt[p] ++;
}

void build(){  //建 AC 自动机
    queue<int> q;
    for(int i = 0; i < 26; i ++){
        if(ch[0][i]) q.push(ch[0][i]);  //根节点儿子入队
    }
    while(q.size()){
        int u = q.front(); q.pop();
        for(int i = 0; i < 26; i ++){
            int v = ch[u][i];
            if(v) ne[v] = ch[ne[u]][i], q.push(v);  //儿子存在，爹帮儿子建回跳边，儿子入队
            else ch[u][i] = ch[ne[u]][i];  //儿子不存在，爹自建转移边
        }
    }
}

int query(string s){  //扫描主串查询
    int ans = 0;
    for(int k = 0, i = 0; k < s.size(); k ++){
        i = ch[i][s[k] - 'a']; 
        for(int j = i; j && ~ cnt[j]; j = ne[j]){
            ans += cnt[j], cnt[j] = -1;  //找到后退出，加速查询
        }
    }
    return ans;
}

例题

搜索关键词

Original Link

给定 $n$ 个长度不超过 $50$ 的由小写英文字母组成的单词，以及一篇长为 $m$ 的文章。

请问，其中有多少个单词在文章中出现了。

注意：每个单词不论在文章中出现多少次，仅累计 1 次。

输入格式

第一行包含整数 $T$，表示共有 $T$ 组测试数据。

对于每组数据，第一行一个整数 $n$，接下去 $n$ 行表示 $n$ 个单词，最后一行输入一个字符串，表示文章。

输出格式

对于每组数据，输出一个占一行的整数，表示有多少个单词在文章中出现。

数据范围

$1\le n \le 10^4, 1\le m \le 10^6$

输入样例：

1
5
she
he
say
shr
her
yasherhs

输出样例：

3

代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 5e5 + 3;

int n;
string s;
int ch[N][26], cnt[N], idx;
int ne[N];

void insert(string s){
    int p = 0;
    for(int i = 0; i < s.size(); i ++){
        int j = s[i] - 'a';
        if(!ch[p][j]) ch[p][j] = ++ idx;
        p = ch[p][j];
    }
    cnt[p] ++;
}

void build(){  //建 AC 自动机
    queue<int> q;
    for(int i = 0; i < 26; i ++){
        if(ch[0][i]) q.push(ch[0][i]);
    }
    while(q.size()){
        int u = q.front(); q.pop();
        for(int i = 0; i < 26; i ++){
            int v = ch[u][i];
            if(v) ne[v] = ch[ne[u]][i], q.push(v);
            else ch[u][i] = ch[ne[u]][i];
        }
    }
}

int query(string s){
    int ans = 0;
    for(int k = 0, i = 0; k < s.size(); k ++){
        i = ch[i][s[k] - 'a'];
        for(int j = i; j && ~ cnt[j]; j = ne[j]){
            ans += cnt[j], cnt[j] = -1;
        }
    }
    return ans;
}

void solve(){

    idx = 0;
    memset(ch, 0, sizeof ch);
    memset(cnt, 0, sizeof cnt);
    memset(ne, 0, sizeof ne);

    cin >> n;
    for(int i = 0; i < n; i ++){
        cin >> s; insert(s);
    }
    build();
    cin >> s;
    cout << query(s) << endl;
}

int main(){
    int _; cin >> _;
    while(_ --) solve();
    return 0;
}

单词

Original Link

某人读论文，一篇论文是由许多单词组成的。

但他发现一个单词会在论文中出现很多次，现在他想知道每个单词分别在论文中出现多少次。

输入格式

第一行一个整数 $N$，表示有多少个单词。

接下来 $N$ 行每行一个单词，单词中只包含小写字母。

输出格式

输出 $N$ 个整数，每个整数占一行，第 $i$ 行的数字表示第 $i$ 个单词在文章中出现了多少次。

数据范围

$1≤N≤200$
所有单词长度的总和不超过 $10^6$。

输入样例：

3
a
aa
aaa

输出样例：

6
3
1

思想：

  • 求每个单词在全文中出现的次数，即该单词在其他单词中出现次数的总和。
  • 故该单词在其他单词中的前缀的后缀即为该单词出现次数的总和。
  • 在建 AC 自动机时利用 BFS 从第 0 层搜索到 n 层，需要保留堆的信息进行递推计算，且递推计算出现的次数时必须逆序。

代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 1e6 + 3;

int n;
string s;
int ch[N][26], cnt[N], idx;
int ne[N], num[N];

int id[N];  //记录

void insert(int x){
    int p = 0;
    for(int i = 0; i < s.size(); i ++){
        int j = s[i] - 'a';
        if(!ch[p][j]) ch[p][j] = ++ idx;
        p = ch[p][j];
        cnt[p] ++;  //统计前缀的次数，每一个结束的位置都代表一个字符串
    }
    id[x] = p;  //记录截止位置
}

void build(){  //建 AC 自动机
    //由于后续递推求前缀出现的次数，故需要保留堆的信息
    int hh = 0, tt = -1;
    for(int i = 0; i < 26; i ++){
        if(ch[0][i]) num[++ tt] = ch[0][i];
    }
    while(hh <= tt){
        int u = num[hh ++];
        for(int i = 0; i < 26; i ++){
            int v = ch[u][i];
            if(v) ne[v] = ch[ne[u]][i], num[++ tt] = v;
            else ch[u][i] = ch[ne[u]][i];
        }
    }
}

void solve(){
    cin >> n;
    for(int i = 0; i < n; i ++){
        cin >> s; insert(i);  //i 为当前单词对应编号
    }
    build();
    //递推更新 cnt, trie 中节点编号为 0 ~ idx，一共 idx + 1 个点，0 既代表根节点又代表空节点
    for(int i = idx; i >= 0; i --) cnt[ne[num[i]]] += cnt[num[i]];  
    for(int i = 0; i < n; i ++) cout << cnt[id[i]] << endl;
}

int main(){
    solve();
    return 0;
}
AC自动机Trie树
暂无评论

发送评论 编辑评论 


				

			

						

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
							
													

					

				

			

			
			

				

					
				

			

				

											

							
							
						

																

							
							
						

																

							
							
						

										
					
											
						

	

		
|´・ω・)ノ
ヾ(≧∇≦*)ゝ
(☆ω☆)
（╯‵□′）╯︵┴─┴
￣﹃￣
(/ω＼)
∠( ᐛ 」∠)＿
(๑•̀ㅁ•́ฅ)
→_→
୧(๑•̀⌄•́๑)૭
٩(ˊᗜˋ*)و
(ノ°ο°)ノ
(´இ皿இ｀)
⌇●﹏●⌇
(ฅ´ω`ฅ)
(╯°A°)╯︵○○○
φ(￣∇￣o)
ヾ(´･ ･｀｡)ノ"
( ง ᵒ̌皿ᵒ̌)ง⁼³₌₃
(ó﹏ò｡)
Σ(っ °Д °;)っ
( ,,´･ω･)ﾉ"(´っω･｀｡)
╮(╯▽╰)╭
o(*////▽////*)q
＞﹏＜
( ๑´•ω•) "(ㆆᴗㆆ)
😂
😀
😅
😊
🙂
🙃
😌
😍
😘
😜
😝
😏
😒
🙄
😳
😡
😔
😫
😱
😭
💩
👻
🙌
🖕
👍
👫
👬
👭
🌚
🌝
🙈
💊
😶
🙏
🍦
🍉
😣
Source: github.com/k4yt3x/flowerhd
	

	

		
颜文字
Emoji
小恐龙
花!
	


									

			

			
			
		

	






上一篇
下一篇 

                    

                    
			        推荐文章
		            

		            

							
4219. 找倍数

							
							

							
D – Circumferences

							
							

							
Codeforces Round #805 (Div. 3)(A~C)

							
							

							
图的存储

							
							

							
1346. 回文平方(进制转换模板)

							
							

							
河南工程学院第六届程序设计竞赛-A组-题解