4.1 质数
概念
4.1.1 试除法判定质数
思想
- $N<2$不是质数
- 从$i=2$开始枚举,直到$\sqrt{n}$,若$i$能被$N$整除,说明不是质数
- 反之,则为质数
模板
bool is_prime(int n){
if(n<2) return 0; //若小于2直接返回false
for(int i=2;i<=n/i;i++){ //优化为sqrt(n)
if(n%i==0) return 0;
}
return 1;
}例题 866. 试除法判定质数
描述
给定 n 个正整数 ai,判定每个数是否是质数。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一个正整数 ai。
输出格式
共 n 行,其中第 i 行输出第 i 个正整数 ai 是否为质数,是则输出 Yes,否则输出 No。
数据范围
1≤n≤100,
1≤ai≤2^31−1
输入样例:
2
2
6输出样例:
Yes
No代码
#include <bits/stdc++.h>
using namespace std;
bool is_prime(int n){
if(n<2) return 0;
for(int i=2;i<=n/i;i++){
if(n%i==0) return 0;
}
return 1;
}
int main(){
int t;
cin>>t;
while(t--){
int x;
cin>>x;
if(is_prime(x)) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
return 0;
}4.1.2 分解质因数
概念
思想
- 算术基本定理:任何一个大于$1$的自然数$N$,如果$N$不为质数
- 那么$N$可以唯一分解成有限个质数的乘积$N=p_1^{a_1}\times p_2^{a_2}\dots\times p_i^{a_k}$,且最多只有一个大于$\sqrt{n}$的质因子
- 这里$p_1<p_2<p_3\dots p_i$均为质数,其中指数$a_k$是正整数
模板
map<int,int> primes; //存储质因子底数和其指数的映射
void get_div(int n){
primes.clear(); //清空数据
for(int i=2;i<=n/i;i++){ //从2开始枚举质因子
if(n%i==0){ //当其为质因子时
while(n%i==0){
primes[i]++; //指数增加
n/=i;
}
}
}
if(n>1) primes[n]++; //剩余的数大于1则为最后的质因子
}例题 867. 分解质因数
描述
给定 n 个正整数 ai,将每个数分解质因数,并按照质因数从小到大的顺序输出每个质因数的底数和指数。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一个正整数 ai。
输出格式
对于每个正整数 ai,按照从小到大的顺序输出其分解质因数后,每个质因数的底数和指数,每个底数和指数占一行。
每个正整数的质因数全部输出完毕后,输出一个空行。
数据范围
1≤n≤100,
2≤ai≤2×109
输入样例:
2
6
8输出样例:
2 1
3 1
2 3代码
#include <bits/stdc++.h>
using namespace std;
map<int,int> primes;
void get_div(int n){
primes.clear();
for(int i=2;i<=n/i;i++){
if(n%i==0){
while(n%i==0){
primes[i]++;
n/=i;
}
}
}
if(n>1) primes[n]++;
}
int main(){
int n;
cin>>n;
while(n--){
int x;
cin>>x;
get_div(x);
for(auto &p : primes) cout<<p.first<<" "<<p.second<<endl;
cout<<endl;
}
return 0;
}4.1.3 线性筛法求质数
思想
- 对于$1\sim N$中的一个合数$n$
- 从小到大枚举筛选出的质数$p$,将$1\sim N$范围内质数$p$的倍数的合数筛掉
- 从而保证了$n$只会被其最小质因子$p_j$筛掉,且一定会在枚举到$p_j\times\frac{n}{p_j}$之前筛掉
模板
int cnt; //记录质数个数
int primes[N]; //存储当前筛选出的质数
bool vis[N]; //标记是否被筛掉
void get_primes(int n){
for(int i=2;i<=n;i++){ //外层从2~n迭代
if(!vis[i]) primes[cnt++]=i; //没有被筛掉说明是质数,记录到primes[N]中
for(int j=0;primes[j]<=n/i;j++){ //将1~n范围内质数primes[j]的i倍的合数筛掉
vis[primes[j]*i]=1; //用最小质因子primes[j]筛掉合数
if(i%primes[j]==0) break;
//i%primes[j]!=0 : 说明primes[j] < i的所有质因子,故primes[j]是primes[j]*i的最小质因子
//i%primes[j]==0 : 说明从小到大枚举到此时的primes[j],一定是i的最小质因子
}
}
}例题 868. 筛质数
描述
给定一个正整数 n,请你求出 1∼n 中质数的个数。
输入格式
共一行,包含整数 n。
输出格式
共一行,包含一个整数,表示 1∼n 中质数的个数。
数据范围
1≤n≤106
输入样例:
8输出样例:
4代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+3;
int cnt; //记录质数个数
int primes[N]; //存储当前筛选出的质数
bool vis[N]; //标记是否被筛掉
void get_primes(int n){
for(int i=2;i<=n;i++){ //外层从2~n迭代
if(!vis[i]) primes[cnt++]=i; //没有被筛掉说明是质数,记录到primes[N]中
for(int j=0;primes[j]<=n/i;j++){ //将1~n范围内质数primes[j]的i倍的合数筛掉
vis[primes[j]*i]=1; //用最小质因子primes[j]筛掉合数
if(i%primes[j]==0) break;
//i%primes[j]!=0 : 说明primes[j] < i的所有质因子,故primes[j]是primes[j]*i的最小质因子
//i%primes[j]==0 : 说明从小到大枚举到此时的primes[j],一定是i的最小质因子
}
}
}
int main(){
int n;
cin>>n;
get_primes(n);
cout<<cnt<<endl;
return 0;
}4.2 约数
概念
4.2.1 试除法求约数
思想
- 从$i=1$开始枚举到$\sqrt{N}$
- $i$和$\frac{N}{i}$即为$N$的约数
模板
const int N=1e6+3;
int res[N]; //存储约数
int cnt; //记录数量
void get_div(int n){
cnt=0; //初始化
for(int i=1;i<=n/i;i++){ //从1开始枚举
if(n%i==0){
res[cnt++]=i; //将i作为约数
if(i!=n/i) res[cnt++]=n/i; //将n/i作为约数
}
}
sort(res,res+cnt); //将约数从小到大排序
}例题 869. 试除法求约数
描述
给定 n 个正整数 ai,对于每个整数 ai,请你按照从小到大的顺序输出它的所有约数。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一个整数 ai。
输出格式
输出共 n 行,其中第 i 行输出第 i 个整数 ai 的所有约数。
数据范围
1≤n≤100,
2≤ai≤2×109
输入样例:
2
6
8输出样例:
1 2 3 6
1 2 4 8 代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+3;
int res[N];
int cnt;
void get_div(int n){
cnt=0;
for(int i=1;i<=n/i;i++){
if(n%i==0){
res[cnt++]=i;
if(i!=n/i) res[cnt++]=n/i;
}
}
sort(res,res+cnt);
}
int main(){
int n;
cin>>n;
while(n--){
int x;
cin>>x;
get_div(x);
for(int i=0;i<cnt;i++) cout<<res[i]<<" ";
cout<<endl;
}
return 0;
}4.2.2 约数个数
思想
-
算术基本定理:任何一个大于$1$的自然数$N$,如果$N$不为质数
-
那么$N$可以唯一分解成有限个质数的乘积$N=p_1^{a_1}\times p_2^{a_2}\dots\times p_i^{a_k}$,且最多只有一个大于$\sqrt{n}$的质因子
-
这里$p_1<p_2<p_3\dots p_n$均为质数,其中指数$a_i$是正整数
-
设$d$为$N$的任意一个约数,$d=p_1^{b_1}\times p_2^{b_2}\dots\times p_i^{b_j}$,其中$0<b_j<a_k$
-
由算术基本定理可知对于$d$中的$p_i^{b_j}$项,$b_j$取值不同,则$d$不同$(每个数的因式分解是唯一的)$
-
故$N$的约数个数$=$$d$的个数$=$$b_j$的选法总数\[
\begin{cases}
p_1共有0\sim a_1种选法\\
p_2共有0\sim a_2种选法\\
p_3共有0\sim a_3种选法\\
p_i共有0\sim a_k种选法\\
\end{cases}
\] -
根据乘法原理可知:$N$的约数个数为$(a_1+1)\times(a_2+1)\times(a_3+1)\times\dots\times(a_k+1)$
模板例题 870. 约数个数
描述
给定 n 个正整数 ai,请你输出这些数的乘积的约数个数,答案对 109+7 取模。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一个整数 ai。
输出格式
输出一个整数,表示所给正整数的乘积的约数个数,答案需对 109+7 取模。
数据范围
1≤n≤100,
1≤ai≤2×109
输入样例:
3
2
6
8输出样例:
12代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL mod=1e9+7;
LL cnt=1;
map<int,int> primes; //存储质因子底数和其指数的映射
void get_div(int n){
for(int i=2;i<=n/i;i++){ //从2开始枚举质因子
if(n%i==0){ //当其为质因子时
while(n%i==0){
primes[i]++; //指数增加
n/=i;
}
}
}
if(n>1) primes[n]++; //剩余的数大于1则为最后的质因子
}
int main(){
int n;
cin>>n;
while(n--){
int x;
cin>>x;
get_div(x);
}
for(auto &p : primes) cnt=cnt*(p.second+1)%mod; //核心:N的约数个数为(a1+1)*(a2+1)*(a3+1)*…*(ai+1)
cout<<cnt<<endl;
return 0;
}4.2.3 约数之和
思想
-
算术基本定理:任何一个大于$1$的自然数$N$,如果$N$不为质数
-
那么$N$可以唯一分解成有限个质数的乘积$N=p_1^{a_1}\times p_2^{a_2}\dots\times p_i^{a_k}$,且最多只有一个大于$\sqrt{n}$的质因子
-
这里$p_1<p_2<p_3\dots p_i$均为质数,其中指数$a_k$是正整数
-
\[
\begin{cases}
p_1的约数之和=p_1^{0}+p_1^{1}+\dots+p_1^{a_1}\\
p_2的约数之和=p_2^{0}+p_2^{1}+\dots+p_2^{a_2}\\
p_3的约数之和=p_3^{0}+p_3^{1}+\dots+p_3^{a_3}\\
p_i的约数之和=p_i^{0}+p_i^{1}+\dots+p_i^{a_k}\\
\end{cases}
\] -
根据乘法原理可知:$N$的约数之和$=(p_1^{0}+p_1^{1}+\dots+p_1^{a_1})\times(p_2^{0}+p_2^{1}+\dots+p_2^{a_2})\times\dots\times(p_i^{0}+p_i^{1}+\dots+p_i^{a_k})$
模板例题 871. 约数之和
描述
给定 n 个正整数 ai,请你输出这些数的乘积的约数之和,答案对 109+7 取模。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一个整数 ai。
输出格式
输出一个整数,表示所给正整数的乘积的约数之和,答案需对 109+7 取模。
数据范围
1≤n≤100,
1≤ai≤2×109
输入样例:
3
2
6
8输出样例:
252代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL mod=1e9+7;
LL res=1;
map<int,int> primes; //存储质因子底数和其指数的映射
void get_div(int n){
for(int i=2;i<=n/i;i++){ //从2开始枚举质因子
if(n%i==0){ //当其为质因子时
while(n%i==0){
primes[i]++; //指数增加
n/=i;
}
}
}
if(n>1) primes[n]++; //剩余的数大于1则为最后的质因子
}
int main(){
int n;
cin>>n;
while(n--){
int x;
cin>>x;
get_div(x);
}
for(auto &p : primes){
LL t=1;
int a=p.first,b=p.second;
while(b--){
t=(t*a+1)%mod; //核心:求出 p0一直加到p的k的次方的和
}
res=res*t%mod;
}
cout<<res<<endl;
return 0;
}4.2.4 最大公约数和最小公倍数
概念
- 最大公约数指两个或多个整数共有约(因)数中最大的数
- 最小公倍数指两个或多个整数的公倍数里最小的数
思想
-
辗转相除法求最大公约数
例如:假如需要求 100 和18 两个正整数的最大公约数,用欧几里得算法,是这样进行的:
100 / 18 = 5 (余 10)
18 / 10= 1(余8)
10 / 8 = 1(余2)
8 / 2 = 4 (余0)
至此,最大公约数为2
以除数和余数反复做除法运算,当余数为 0 时,取当前算式除数为最大公约数,所以就得出了 100 和 18 的最大公约数2。 -
求$N$和$M$的最小公倍数$lcm(N,M)$,则先求$N$和$M$的最大公约数$gcd(N,M)$,然后$\frac{N\times M}{gcd(N,M)}$则为最小公倍数。
模板
//最大公约数
int gcd(int a, int b){
return b ? gcd(b, a % b) : a;
}
//最小公倍数
int lcm(int a,int b){
return a/gcd(a,b)*b;
}4.3 欧拉函数
概念
- $1∼N$中与$N$互质的数的个数被称为欧拉函数,记为 $\phi(N)$,特别的$\phi(1)=1$
- 欧拉函数是一个积性函数,若$m$,$n$互质,则有$\phi(m\times n)=\phi(m)\times\phi(n)$
4.3.1 公式法求欧拉函数
思想
-
算术基本定理:任何一个大于$1$的自然数$N$,如果$N$不为质数
-
那么$N$可以唯一分解成有限个质数的乘积$N=p_1^{a_1}\times p_2^{a_2}\dots\times p_i^{a_k}$,且最多只有一个大于$\sqrt{n}$的质因子
-
这里$p_1<p_2<p_3\dots p_i$均为质数,其中指数$a_k$是正整数
-
则$\phi(N)=\phi(p_1^{a_1})\times\phi(p_2^{a_2})\times\dots\times\phi(p_n^{a_n})$
-
对于任意一项$\phi(p_i^{a_i})$,与$p_i^{a_i}$不互质的数有$p_i,2\times p_i,3\times p_i,\dots,p_i^{(a_i-1)}\times p_i$共$p_i^{(a_i-1)}$项
-
即$\phi(p_i^{a_i})=p_i^{a_i}-p_i^{(a_i-1)}$
-
\[
\begin{aligned}
\phi(N)&=\phi(p_1^{a_1})\times\phi(p_2^{a_2})\times\dots\times\phi(p_n^{a_n})\\
&=(p_1^{a_1}-p_1^{(a_1-1)})\times(p_2^{a_2}-p_2^{(a_2-1)})\times\dots\times(p_n^{a_n}-p_n^{(a_n-1)})\\
&=p_1^{a_1}\times p_2^{a_2}\times\dots\times p_n^{a_n}\times(1-\frac{1}{p_1})\times(1-\frac{1}{p_2})\times\dots\times(1-\frac{1}{p_n})\\
&=N\times\prod^{n}_{i=1}{(1-\frac{1}{p_i})}
\end{aligned}
\]
模板
typedef long long LL;
LL phi(LL n){
LL res=n;
for(int i=2;i<=n/i;i++){
if(n%i==0){
res=res/i*(i-1); //(1-1/i)转换为(i-1)/i
while(n%i==0) n/=i;
}
}
if(n>1) res=res/n*(n-1);
return res;
}例题 873. 欧拉函数
描述
给定 n 个正整数 ai,请你求出每个数的欧拉函数。
欧拉函数的定义
1∼N 中与 N 互质的数的个数被称为欧拉函数,记为 ϕ(N)。
若在算数基本定理中,N=pa11pa22…pamm,则:
ϕ(N) = N×p1−1p1×p2−1p2×…×pm−1pm
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一个正整数 ai。
输出格式
输出共 n 行,每行输出一个正整数 ai 的欧拉函数。
数据范围
1≤n≤100,
1≤ai≤2×109
输入样例:
3
3
6
8输出样例:
2
2
4代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL phi(LL n){
LL res=n;
for(int i=2;i<=n/i;i++){
if(n%i==0){
res=res/i*(i-1);
while(n%i==0) n/=i;
}
}
if(n>1) res=res/n*(n-1);
return res;
}
int main(){
int n;
cin>>n;
while(n--){
int x;
cin>>x;
cout<<phi(x)<<endl;
}
return 0;
}4.3.2 筛法求欧拉函数
思想
- 利用线性筛,在筛选$1\sim N$中的质数时,将$1\sim N$的欧拉函数$\phi(P_i)$求出
- 对于质数$P_i$,其$\phi(P_i)=P\times(1-\frac{1}{P})=P-1$
- 对于合数$P_i$,其\[\phi(P_i)=N\times\prod^{n}_{i=1}{(1-\frac{1}{p_i})}\]
- 在线性筛法求质数的模板中利用最小质因子筛掉合数的过程时:
- 当$i\%primes[j]=0$时,说明$primes[j]$是$i$的一个质因子,且$primes[j]$是$primes[j]\times i$的一个质因子,故$\phi(i)$包含$(1-\frac{1}{primes[j]})$的情况,即$\phi(primes[j]\times i)=primes[j]\times\phi(i)$
- 当$i\%primes[j]\ne 0$时 ,说明$primes[j]$是$i$的最小质因子,且$primes[j]$不是$primes[j]\times i$的一个质因子,故$\phi(i)$不包含$(1-\frac{1}{primes[j]})$的情况,即$\begin{aligned}\phi(primes[j]\times i)&=primes[j]\times\phi(i)\times(1-\frac{1}{primes[j]})\ &=(primes[j]-1)\times\phi(i)\end{aligned}$
模板
int primes[N]; //存储当前筛选出的质数
bool vis[N]; //标记是否被筛掉
int phi[N]; //记录欧拉函数的值
int cnt; //记录质数个数
void get_phi(int n){
phi[1]=1; //特别的,phi[1]=1
for(int i=2;i<=n;i++){
if(!vis[i]){
primes[cnt++]=i; //没有被筛掉说明是质数,记录到primes[N]中
phi[i]=i-1; //质数的欧拉函数的情况
}
for(int j=0;primes[j]<=n/i;j++){ //将1~n范围内质数primes[j]的i倍的合数筛掉
vis[primes[j]*i]=1;
if(i%primes[j]==0){ //用最小质因子primes[j]筛掉合数
phi[primes[j]*i]=primes[j]*phi[i]; //包含(1-1/primes[j])的情况
break;
}
else phi[primes[j]*i]=(primes[j]-1)*phi[i]; //不包含(1-1/primes[j])的情况
}
}
}例题 874. 筛法求欧拉函数
描述
给定一个正整数 n,求 1∼n 中每个数的欧拉函数之和。
输入格式
共一行,包含一个整数 n。
输出格式
共一行,包含一个整数,表示 1∼n 中每个数的欧拉函数之和。
数据范围
1≤n≤106
输入样例:
6输出样例:
12代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+3;
typedef long long LL;
int primes[N];
bool vis[N];
int phi[N];
int cnt;
void get_phi(int n){
phi[1]=1;
for(int i=2;i<=n;i++){
if(!vis[i]){
primes[cnt++]=i;
phi[i]=i-1;
}
for(int j=0;primes[j]<=n/i;j++){
vis[primes[j]*i]=1;
if(i%primes[j]==0){
phi[primes[j]*i]=primes[j]*phi[i];
break;
}
else phi[primes[j]*i]=(primes[j]-1)*phi[i];
}
}
}
int main(){
int n;
cin>>n;
get_phi(n);
LL res=0;
for(int i=1;i<=n;i++){
res+=phi[i];
}
cout<<res<<endl;
return 0;
}4.4 快速幂
概念
- 快速求出$a^k\mod p$的结果
思想
- 预处理出$a^{2^0},a^{2^1},a^{2^2}\dots a^{2^{log_2^k}}$的结果
- 则使得$k=2^{p_1}+2^{p_2}+\dots+2^{p_i}$
- 即:$a^k=a^{2^{p_1}}\times a^{2^{p_2}}\times\dots\times a^{2^{p_i}}$
- 对于$a^{2^0}\times a^{2^0}=a^{2^{1}},a^{2^{1}}\times a^{2^{1}}=a^{2^{2}}$,即\[a^{2^{p_i}}=a^{2^{p_{i-1}}}\times a^{2^{p_{i-1}}}\]
- 综上所述,在操作时记录$a^{p_i}$的值,和累乘的结果
- 将$k$化为二进制表示,按位
>>操作,若当前位是$1$,则对当前累乘的结果$\times a^{p_i} \mod p$ - 每次对\[k\]进行按位
>>操作后,更新\[a^{p_{i+1}}=a^{p_i}\times a^{p_i}\mod p\] - 当二进制下的$k$无法再
>>时,累乘结果即为答案
模板
typedef long long LL;
LL qmi(LL a,LL k,LL p){ //计算 a^k % p 的结果
LL res=1; //记录累乘结果
while(k){
if(k&1) res=res*a%p; //k&1得到当前位,若为1则累乘a^pi
a=a*a%p; //更新a^pi
k>>=1; //右移1位
}
return res;
}4.4.1 快速幂求逆元
概念
- 同余:设$m$为正整数,$a$和$b$是整数,若$m|a-b$,则称$a$模$m$同余于$b$,或$a$与$b$模$m$同余,记作$a\equiv b(mod~m)$
- 若$ab\equiv 1(mod~m)$,则称$b$为$a$的模$m$逆,记作$a^{-1}(mod~m)$或$a^{-1}$
注意
-
$a$的模$m$逆存在 $\Leftrightarrow$ $a$与$m$互质
-
当$m$为质数时,用费马小定理求
-
当$m$不为质数时,用扩展欧几里得算法求
思想
-
利用快速幂实现$m$为质数时用费马小定理求逆元
-
费马小定理:设$p$为素数,且$a$与$p$互质,则$a^{p^{-1}}\equiv 1(mod~p)$
-
\[
\begin{aligned}
a^{p^{-1}}\equiv 1(mod~p) \rightarrow &a\times a^{p^{-2}}\equiv 1(mod~p)\\
&a\times b\equiv 1(mod~p)\\
&即:b=a^{p^{-2}}
\end{aligned}
\]
模板例题 876. 快速幂求逆元
描述
给定 n 组 ai,pi,其中 pi 是质数,求 ai 模 pi 的乘法逆元,若逆元不存在则输出 impossible。
注意:请返回在 0∼p−1 之间的逆元。
乘法逆元的定义
若整数 b,m 互质,并且对于任意的整数 a,如果满足 b|a,则存在一个整数 x,使得 a/b≡a×x(modm),则称 x 为 b 的模 m 乘法逆元,记为 b−1(modm)。
b 存在乘法逆元的充要条件是 b 与模数 m 互质。当模数 m 为质数时,bm−2 即为 b 的乘法逆元。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一个数组 ai,pi,数据保证 pi 是质数。
输出格式
输出共 n 行,每组数据输出一个结果,每个结果占一行。
若 ai 模 pi 的乘法逆元存在,则输出一个整数,表示逆元,否则输出 impossible。
数据范围
1≤n≤105,
1≤ai,pi≤2∗109
输入样例:
3
4 3
8 5
6 3输出样例:
1
2
impossible代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL qmi(LL a,LL k,LL p){
LL res=1;
while(k){
if(k&1) res=res*a%p;
a=a*a%p;
k>>=1;
}
return res;
}
int main(){
int n;
cin>>n;
while(n--){
int a,p;
cin>>a>>p;
if(a%p==0) cout<<"impossible"<<endl; //a与p不互质则说明无逆元
else cout<<qmi(a,p-2,p)<<endl;
}
return 0;
}4.5 扩展欧几里得算法
思想
-
欧几里得算法:$gcd(a,b)=gcd(b,a\%b)$,特别的$gcd(a,0)=a$
-
裴蜀定理:对于任意正整数$a,b$,一定存在非零的$x,y$,使得$ax+by=gcd(a,b)$
-
\[
\begin{cases}
b=0时:\begin{cases}
gcd(a,b)=a\\ax+by=gcd(a,b)\\
\end{cases}\Rightarrow\begin{cases}x=1\\y=0\end{cases}
\\
\\
\\
\\
\\
b\neq0时:
\begin{cases}
\begin{aligned}
①&设~ax+by=gcd(a,b)=d\\
&\because 由欧几里得算法可知:gcd(a,b)=gcd(b,a\%b)=d\\
&\therefore 由裴蜀定理得:b{x}'+(a\%b){y}'=d\\
又&\because ax+by=d\\
&\therefore联立
\begin{cases}
ax+by=d\\b{x}'+(a\%b){y}'=d\\a\%b=a-\lfloor\frac{a}{b}\rfloor b
\end{cases}\Rightarrow\begin{cases}x={y}'\\y={x}'-\lfloor\frac{a}{b}\rfloor{y}'\end{cases}\\
②&设{a}'=b,{b}'=a\%b\\
&\therefore gcd(b,a\%b)=gcd({a}',{b}')=d\\
&\because gcd({a}',{b}')=gcd({b}',{a}'\%{b}')=d\\
&\therefore {b}'{x}''+{a}'\%{b}'{y}''=d\\
又&\because b{x}'+(a\%b){y}'=d\\
&\therefore联立\begin{cases}
b{x}'+(a\%b){y}'=d\\{b}'{x}''+{a}'\%{b}'{y}''=d\\{a}'\%{b}'={a}'-\lfloor\frac{{a}'}{{b}'}\rfloor{b}'
\end{cases}\Rightarrow\begin{cases}{x}'={y}''\\{y}'={x}''-\lfloor\frac{{a}'}{{b}'}\rfloor{y}''
\end{cases}\\
③&设{a}''={b}',{b}''={a}'\%{b}'\\
&\dots\\
&\dots\\
&直到b=0时,联立解得\begin{cases}{x}^i=1\\{y}^i=0\end{cases}\\
&然后逐步返回每一次联立所得的结果\begin{cases}{x}^{i-1}={y}^{i}\\{y}^{i-1}={x}^{i}-\lfloor\frac{{a}^{i}}{{b}^i}\rfloor{y}^{i}
&最后返回得到x和y的值
\end{cases}\\
\end{aligned}
\end{cases}
\end{cases}
\]
注意
-
当方程符合$ax+by=gcd(a,b)$的形式时,才可以用扩展欧几里得算法求解$(x_0,y_0)$
-
推论:可以进一步求解任意方程$ax+by=n$,得到一个整数解
-
\[
\begin{aligned}
\begin{cases}
&(1)~~判断方程ax+by=n是否有整数解,有解的条件为:gcd(a,b)可以整除n\\
&(2)~~用扩展欧几里得算法求ax+by=gcd(a,b)得到一个解(x_0,y_0)\\
&(3)~~在ax_0+by_0=gcd(a,b)两边同时乘\frac{n}{gcd(a,b)}\Rightarrow\frac{ax_0n}{gcd(a,b)}+\frac{by_0n}{gcd(a,b)}=n\\
&(4)~~对照ax+by=n可知该方程的一个解为({x}',{y}'),其中\begin{cases}{x}'=\frac{x_0n}{gcd(a,b)}\\{y}'=\frac{y_0n}{gcd(a,b)} \end{cases}
\end{cases}
\end{aligned}
\]
模板
void exgcd(int a,int b,int &x,int &y){
if(!b){ //若b=0时
x=1,y=0;
return ;
}
else{ //b!=0时
exgcd(b,a%b,x,y); //递归到下一层
int t=x; //返回时执行
x=y;
y=t-a/b*y;
}
}例题 877. 扩展欧几里得算法
描述
给定 n 对正整数 ai,bi,对于每对数,求出一组 xi,yi,使其满足 ai×xi+bi×yi=gcd(ai,bi)。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含两个整数 ai,bi。
输出格式
输出共 n 行,对于每组 ai,bi,求出一组满足条件的 xi,yi,每组结果占一行。
本题答案不唯一,输出任意满足条件的 xi,yi 均可。
数据范围
1≤n≤105,
1≤ai,bi≤2×109
输入样例:
2
4 6
8 18输出样例:
-1 1
-2 1代码
#include <bits/stdc++.h>
using namespace std;
void exgcd(int a,int b,int &x,int &y){
if(!b){
x=1,y=0;
return ;
}
else{
exgcd(b,a%b,x,y);
int t=x;
x=y;
y=t-a/b*y;
}
}
int main(){
int n;
cin>>n;
while(n--){
int a,b,x,y;
cin>>a>>b;
exgcd(a,b,x,y);
cout<<x<<" "<<y<<endl;
}
return 0;
}4.5.1 解一元线性同余方程
概念
- $ax\equiv b(mod~m)$,即$\frac{ax}{m}$与$\frac{b}{m}$的余数相同,且$a,b,m$为整数,求$x$的值
- 该方程即为一元线性同余方程
思想
-
对$ax\equiv b(mod~m)$做等价变形:$ax+my=b$
-
\[
\begin{aligned}
&\because &ax&\equiv b(mod~m)\\
&\therefore &ax\%m&=k(b\%m),(k\in \Z)\\
&\therefore &ax-\lfloor\frac{ax}{m}\rfloor m&=k(b-\lfloor\frac{b}{m}\rfloor m)\\
&\therefore &ax-kb&=(\lfloor\frac{ax}{m}\rfloor-k\lfloor\frac{b}{m}\rfloor)m\\
&\because &\lfloor\frac{ax}{m}\rfloor,&\lfloor\frac{b}{m}\rfloor,k\in \Z\\
&\therefore &(\lfloor\frac{ax}{m}\rfloor&-k\lfloor\frac{b}{m}\rfloor)\in \Z\\
&&设(\lfloor\frac{ax}{m}\rfloor&-k\lfloor\frac{b}{m}\rfloor)=y,(y\in \Z)\\
&\therefore &ax-kb&=my\Rightarrow ax-my=b\\
又&\because &y&可以为负数\\
&\therefore &ax\equiv b(mod~&m)\leftrightarrow ax+my=b
\end{aligned}
\] -
由扩展欧几里得算法的推论可知:当且仅当$ gcd(a,m)$可以整除$b$时,$ax+my=b$存在整数解
-
\[
由扩展欧几里得算法可知:
\begin{cases}
当gcd(a,m)=b时:\begin{cases}x=x_0\\y=y_0\end{cases}\\
当gcd(a,m)为b的整数倍时:\begin{cases}{x}'=\frac{x_0b}{gcd(a,m)}\\{y}'=\frac{y_0b}{gcd(a,m)}\end{cases}
\end{cases}
\]
例题 878. 线性同余方程
描述
给定 n 组数据 ai,bi,mi,对于每组数求出一个 xi,使其满足 ai×xi≡bi(modmi),如果无解则输出 impossible。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一组数据 ai,bi,mi。
输出格式
输出共 n 行,每组数据输出一个整数表示一个满足条件的 xi,如果无解则输出 impossible。
每组数据结果占一行,结果可能不唯一,输出任意一个满足条件的结果均可。
输出答案必须在 int 范围之内。
数据范围
1≤n≤105,
1≤ai,bi,mi≤2×109
2
2 3 6
4 3 5输出样例:
输出样例:
impossible
-3代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
void exgcd(LL a,LL b,LL &x,LL &y){
if(!b){ //若b=0时
x=1,y=0;
return ;
}
else{
exgcd(b,a%b,x,y);
LL t=x;
x=y;
y=t-a/b*y;
}
}
LL gcd(LL a,LL b){
return b ? gcd(b,a%b) : a;
}
int main(){
int n;
cin>>n;
while(n--){
LL a,b,m,x,y;
cin>>a>>b>>m;
LL d=gcd(a,m);
exgcd(a,m,x,y);
if(b%d) cout<<"impossible"<<endl;
else cout<<b/d*x%m<<endl;
}
return 0;
}
4.6 中国剩余定理
概念
-
若存在整数$m_1,m_2,m_3\dots m_n$两两互质,则对于任意的整数$a_1,a_2,a_3\dots a_n$,一元线性同余方程组$(S)$有通解
-
\[
(S):
\begin{cases}
x\equiv a_1(mod~m_1)\\
x\equiv a_2(mod~m_2)\\
x\equiv a_3(mod~m_3)\\
\dots\\
x\equiv a_n(mod~m_n)\\
\end{cases}
\]
思想
-
对于$(S)$其中的两个式子进行合并
-
\[
\begin{cases}
x\equiv a_1(mod~m_1)\\
x\equiv a_2(mod~m_2)\\
\end{cases}
\Rightarrow
\begin{cases}
x=k_1m_1+a_1\\
x=k_2m_2+a_2\\
\end{cases}
\] -
将等价转换后的两式进行联立,化简得$k_1m_1+k_2(-m_2)=a_2-a_1~①$
-
由扩展欧几里得算法可以得到一组解$({k_1}',{k_2}')$,使得:${k_1}'m_1+{k_2}'(-m_2)=gcd(m_1,-m_2)$
-
若$gcd(m_1,-m_2)$不能整除$a2-a1$,则无解,否则有通解
-
设$gcd(m_1,-m_2)=d,y=\frac{(a_2-a_1)}{d}$
-
由扩展欧几里得算法的推论可知:\[\begin{cases}k_1={k_1}'y\\k_2={k_2}'y\end{cases}\]
-
引入通解\[\begin{cases}k_1={k_1}+k\frac{m_2}{d}\\k_2={k_2}+\frac{m_1}d\end{cases}\],$k\in \Z$
-
将通解带入$①$得$({k_1}+k\frac{m_2}{d})m_1+({k_2}+k\frac{m_1}{d})(-m_2)=a_2-a_1$
-
化简得$k_1m_1+k_2(-m_2)=a_2-a_1$和$①$相同,故成立
-
重复上述步骤,不断合并剩余的式子,即可得到最终的通解
例题 204. 表达整数的奇怪方式
描述
给定 2n 个整数 a1,a2,…,an 和 m1,m2,…,mn,求一个最小的非负整数 x,满足 ∀i∈[1,n],x≡mi(mod ai)。
输入格式
第 1 行包含整数 n。
第 2…n+1 行:每 i+1 行包含两个整数 ai 和 mi,数之间用空格隔开。
输出格式
输出最小非负整数 x,如果 x 不存在,则输出 −1。
如果存在 x,则数据保证 x 一定在 64 位整数范围内。
数据范围
1≤ai≤231−1,
0≤mi<ai
1≤n≤25
输入样例:
2
8 7
11 9输出样例:
31代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
void exgcd(LL a,LL b, LL &x,LL &y){
if(!b){
x=1,y=0;
return ;
}
else{
exgcd(b,a%b,x,y);
LL t=x;
x=y;
y=t-a/b*y;
}
}
LL gcd(LL a,LL b){
return b ? gcd(b,a%b) : a;
}
int main(){
int n;
cin>>n;
LL x=0,m1,a1; //第一个方程的系数 备份数据
cin>>m1>>a1; //先输入第一个方程
for(int i=0;i<n-1;i++){ //合并接下来的n-1个方程
LL m2,a2;
cin>>m2>>a2;
LL k1,k2;
LL d=gcd(m1,m2);
exgcd(m1,m2,k1,k2);
if((a2-a1)%d){ //此时无解
x=-1;
break;
}
k1*=(a2-a1)/d;//特解
k1=(k1%(m2/d)+m2/d)%(m2/d); //让特解k1取到最小正整数解
x=k1*m1+a1;
LL m=abs(m1/d*m2);
a1=k1*m1+a1;
m1=m;
}
if(x!=-1) x=(a1%m1+m1)%m1 //当循环结束时,此时的值应该与最小公倍数取模,以求得最小正整数解
cout<<x<<endl;
return 0;
}4.7 高斯消元
概念
-
利用初等行(列)变换,对一组线性方程组进行消元,把增广矩阵化为阶梯型矩阵
-
\[
\begin{aligned}
已知某线&性方程组:\\\\
&\begin{cases}
a_{11}x_1+a_{12}x_2+\dots+a_{1n}x_n=b_1\\
a_{21}x_1+a_{22}x_2+\dots+a_{2n}x_n=b_2\\
\dots\\
a_{n1}x_1+a_{n2}x_2+\dots+a_{nn}x_n=b_n\\
\end{cases}\\\\
增广矩阵&为:\\\\
&\begin{pmatrix}
a_{11}&a_{12}&\dots&a_{1n}&b_1\\
a_{21}&a_{22}&\dots&a_{2n}&b_2\\
\vdots&\vdots&\vdots&\vdots&\vdots\\
a_{n1}&a_{n2}&\dots&a_{nn}&b_n\\
\end{pmatrix}\\\\
运用初等&行变换:\\\\
&\begin{pmatrix}
a_{11}&a_{12}&\dots&a_{1n}&b_1\\
&a_{22}&a_{2(i+1)}&a_{2n}&b_2\\
&&&\vdots&\vdots\\
&&&a_{nn}&b_n\\
\end{pmatrix}\\\\
\end{aligned}\\
解的情况
\begin{cases}
无解:若在最后化成的上三角形矩阵中,正对角线中某个元素为0,\\但其所在行的最后一列元素不为0时,此时矩阵无解\\\\有无数解:若在最后化成的上三角形矩阵中,\\存在正对角线中某个元素为0,\\且其所在行的最后一列元素也为0时,\\此时矩阵有无穷组解 \\\\有唯一解:若在最后化成的上三角形矩阵中,不存在正对角线中某个元素为0,\\此时矩阵有唯一解\\
\end{cases}
\]
初等行(列)变换
- 某一行乘上一个非零数,矩阵不变
- 某一行乘上一个常数加到另一行上,矩阵不变
- 交换矩阵中某两行的元素,矩阵不变
思想
- 对增广矩阵的每一列$c_i$进行枚举,找到当前的列中绝对值最大的元素所在的行$r_i$
- 将$r_i$行与最上方未确定阶梯型的行进行交换
- 用初等行变换将$r_i$行变为原来的$k$倍,且使得变换后, $r_i$行的第一个数变成$1$
- 继续用初等行变换,将$r_i$行下方的所有的行的$c_i$列的值变为$0$
- 重复上述步骤,直到最终得到阶梯型矩阵,判断解的情况
- 若有解,则从最后一行向上回代,得出方程组的解
模板
const int N=110;
const double eps=1e-8;
int n;
double a[N][N];
int gauss(){
int c,r;
for (c=0,r=0;c<n;c++){
int t=r;
for(int i=r;i<n;i++){ //筛选出所在列元素最大的行
if(fabs(a[i][c])>fabs(a[t][c])) t=i;
}
if(fabs(a[t][c])<eps) continue; //正对角线中有元素为0,这时有无穷解和无解
if(t!=r) for(int i=c;i<=n;i++) swap(a[t][i],a[r][i]); //若t改变,则交换两行
for(int i=n;i>=c;i--) a[r][i]/=a[r][c]; //将所在行所在列元素变为1
for(int i=r+1;i<n;i++){ //将所在行所在列的下方的行的所在列元素变为0
if(fabs(a[i][c])>eps){
for(int j=n;j>=c;j--) a[i][j]-=a[r][j]*a[i][c];
}
}
r++;
}
if(r<n){ //row<n,即对角线中元素为0的行未被算上
for(int i=r;i<n;i++){
if(fabs(a[i][n])>eps) return 2;
}
return 1;
}
for(int i=n-1;i>=0;i--){ //将非主元位置的A系数矩阵的其他x消去
for(int j=i+1;j<n;j++) a[i][n]-=a[j][n]*a[i][j];
}
return 0;
}4.7.1 高斯消元解线性方程组
模板例题 883. 高斯消元解线性方程组
描述
输入一个包含 n 个方程 n 个未知数的线性方程组。
方程组中的系数为实数。
求解这个方程组。
下图为一个包含 m 个方程 n 个未知数的线性方程组示例:
\[
\begin{cases}
a_{11}x_1+a_{12}x_2+\dots+a_{1n}x_n=b_1\\
a_{21}x_1+a_{22}x_2+\dots+a_{2n}x_n=b_2\\
\dots\\
a_{m1}x_1+a_{m2}x_2+\dots+a_{mn}x_n=b_n\\
\end{cases}\\\\
\]
输入格式
第一行包含整数 n。
接下来 n 行,每行包含 n+1 个实数,表示一个方程的 n 个系数以及等号右侧的常数。
输出格式
如果给定线性方程组存在唯一解,则输出共 n 行,其中第 i 行输出第 i 个未知数的解,结果保留两位小数。
如果给定线性方程组存在无数解,则输出 Infinite group solutions。
如果给定线性方程组无解,则输出 No solution。
数据范围
1≤n≤100,
所有输入系数以及常数均保留两位小数,绝对值均不超过 100。
输入样例:
3
1.00 2.00 -1.00 -6.00
2.00 1.00 -3.00 -9.00
-1.00 -1.00 2.00 7.00输出样例:
1.00
-2.00
3.00分析
\[
\begin{aligned}
由样例可&得增广矩阵:\\\\
&\begin{pmatrix}
1&2&-1&-6\\
2&1&-3&-9\\
-1&-1&2&7\\
\end{pmatrix}\\\\c_1中绝对&值最大元素位于r_2,将r_2与r_1交换:\\\\
&\begin{pmatrix}
2&1&-3&-9\\
1&2&-1&-6\\
-1&-1&2&7\\
\end{pmatrix}\\\\
将r_1的第&c_1列元素变为1,需要使得r_1\times \frac{1}{2}:\\\\
&\begin{pmatrix}
1&0.5&-1.5&-4.5\\
1&2&-1&-6\\
-1&-1&2&7\\
\end{pmatrix}\\\\
利用初等&行变换将r_1下方的所有的行的c_1列变为0:\\
&即执行r_2-r_1、r_3+r_1\\\\
&\begin{pmatrix}
1&0.5&-1.5&-4.5\\
0&1.5&0.5&-1.5\\
0&-0.5&0.5&2.5\\
\end{pmatrix}\\\\
此时r_1已&确定为阶梯矩阵的行,从r_1下方继续枚举,\\
c_2中绝对&值最大的元素位于r_2,由于r_2上方无未确\\
定的阶梯&矩阵的行,故不需要交换。\\
将r_2的第&c_2列元素变为1,需要使得r_2\times \frac{2}{3}:\\\\
&\begin{pmatrix}
1&0.5&-1.5&-4.5\\
0&1&\frac{1}{3}&-1\\
0&-0.5&0.5&2.5\\
\end{pmatrix}\\\\
利用初等&行变换将r_2下方的所有的行的c_2列变为0:\\
&即执行r_3+r_2\times\frac{1}{2}\\\\
&\begin{pmatrix}
1&0.5&-1.5&-4.5\\
0&1&\frac{1}{3}&-1\\
0&0&\frac{2}{3}&2\\
\end{pmatrix}\\\\
此时r_2已&确定为阶梯矩阵的行,从r_2下方继续枚举,\\
r_3为最后&一行,将r_3的第c_3列元素变为1,需要使得r_3\times \frac{3}{2}:\\\\
&\begin{pmatrix}
1&0.5&-1.5&-4.5\\
0&1&\frac{1}{3}&-1\\
0&0&1&3\\
\end{pmatrix}\\\\
判断该上&三角矩阵中不存在正对角线中某个元素为0,此时\\
矩阵有唯&一解,x_3=3,从r_2进行回代:\\
&即执行r_2-r_3\times\frac{1}{3}\\\\
&\begin{pmatrix}
1&0.5&-1.5&-4.5\\
0&1&0&-2\\
0&0&1&3\\
\end{pmatrix}\\\\
此时可得&x_2=-2,回代r_1:\\
&即执行r_1-r_2\times\frac{1}{2}+r_3\times\frac{3}{2}\\\\
&\begin{pmatrix}
1&0&0&1\\
0&1&0&-2\\
0&0&1&3\\
\end{pmatrix}\\\\
此时可得&x_1=1,综上可得:
\begin{cases}
x_1=1\\x_2=-2\\x_3=3
\end{cases}
\end{aligned}
\]
代码
#include <bits/stdc++.h>
using namespace std;
const int N=110;
const double eps=1e-8;
int n;
double a[N][N];
int gauss(){
int c,r;
for (c=0,r=0;c<n;c++){
int t=r;
for(int i=r;i<n;i++){ //筛选出所在列元素最大的行
if(fabs(a[i][c])>fabs(a[t][c])) t=i;
}
if(fabs(a[t][c])<eps) continue; //正对角线中有元素为0,这时有无穷解和无解
if(t!=r) for(int i=c;i<=n;i++) swap(a[t][i],a[r][i]); //若t改变,则交换两行
for(int i=n;i>=c;i--) a[r][i]/=a[r][c]; //将所在行所在列元素变为1
for(int i=r+1;i<n;i++){ //将所在行所在列的下方的行的所在列元素变为0
if(fabs(a[i][c])>eps){
for(int j=n;j>=c;j--) a[i][j]-=a[r][j]*a[i][c];
}
}
r++;
}
if(r<n){ //row<n,即对角线中元素为0的行未被算上
for(int i=r;i<n;i++){
if(fabs(a[i][n])>eps) return 2;
}
return 1;
}
for(int i=n-1;i>=0;i--){ //将非主元位置的A系数矩阵的其他x消去
for(int j=i+1;j<n;j++) a[i][n]-=a[j][n]*a[i][j];
}
return 0;
}
int main(){
cin>>n;
for(int i=0;i<n;i++){
for(int j=0;j<=n;j++){
cin>>a[i][j];
}
}
int t=gauss();
if(t==2){
cout<<"No solution"<<endl;
}
else if(t==1) cout<<"Infinite group solutions"<<endl;
else{
for(int i=0;i<n;i++){
if(fabs(a[i][n])<eps) a[i][n]=0;
printf("%.2lf\n",a[i][n]);
}
}
return 0;
}4.7.2 高斯消元解异或线性方程组
思想
- 将解线性方程组的计算化为异或运算
模板例题 884. 高斯消元解异或线性方程组
描述
输入一个包含 n 个方程 n 个未知数的异或线性方程组。
方程组中的系数和常数为 0 或 1,每个未知数的取值也为 0 或 1。
求解这个方程组。
异或线性方程组示例如下:
M[1][1]x[1] ^ M[1][2]x[2] ^ … ^ M[1][n]x[n] = B[1]
M[2][1]x[1] ^ M[2][2]x[2] ^ … ^ M[2][n]x[n] = B[2]
…
M[n][1]x[1] ^ M[n][2]x[2] ^ … ^ M[n][n]x[n] = B[n]
其中 ^ 表示异或(XOR),M[i][j] 表示第 i 个式子中 x[j] 的系数,B[i] 是第 i 个方程右端的常数,取值均为 0 或 1。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含 n+1 个整数 0 或 1,表示一个方程的 n 个系数以及等号右侧的常数。
输出格式
如果给定线性方程组存在唯一解,则输出共 n 行,其中第 i 行输出第 i 个未知数的解。
如果给定线性方程组存在多组解,则输出 Multiple sets of solutions。
如果给定线性方程组无解,则输出 No solution。
数据范围
1≤n≤100
输入样例:
3
1 1 0 1
0 1 1 0
1 0 0 1输出样例:
1
0
0代码
#include <bits/stdc++.h>
using namespace std;
const int N=110;
int n;
int a[N][N];
int guass(){
int c,r;
for (c=0,r=0;c<n;c++){
int t=r;
for (int i=r;i<n;i++){
if (a[i][c]) t = i;
}
if(!a[t][c]) continue;
for (int i=c;i<=n;i++) swap(a[r][i],a[t][i]);
for (int i=r+1;i<n;i++){
if (a[i][c]){
for (int j=n;j>=c;j--) a[i][j]^=a[r][j];
}
}
r++;
}
if(r<n){
for(int i=r;i<n;i++){
if(a[i][n]) return 2;
}
return 1;
}
for(int i=n-1;i>=0;i--){
for(int j=i+1;j<n;j++){
a[i][n]^=a[i][j]*a[j][n];
}
}
return 0;
}
int main(){
cin>>n;
for(int i=0;i<n;i++){
for(int j=0;j<n+1;j++){
cin>>a[i][j];
}
}
int t=guass();
if(t==0){
for(int i=0;i<n;i++) cout<<a[i][n]<<endl;
}
else if(t==1) cout<<"Multiple sets of solutions"<<endl;
else cout<<"No solution"<<endl;
return 0;
}4.8 组合数
概念
- 从$n$个不同元素中每次取出$m$个不同元素,不管其顺序合成一组,称为从$n$个元素中不重复地选取$m$个元素的一个组合。
- 所有这样的组合的种数称为组合数
公式
- $C_{n}^{m}=\frac{n!}{m!(n-m)!},C_n^0=C_n^n=1$
- $C_n^m=C_n^{n-m}$
- \[C_n^m=C_{n-1}^m+C_{n-1}^{m-1}\]
- $C_n^0+C_n^1+C_n^2+\dots+C_n^n=2^n$
4.8.1 求组合数 I
思想
- \[C_n^m=C_{n-1}^m+C_{n-1}^{m-1}\]
- 递推公式求组合数
模板例题 885. 求组合数 I
给定 n 组询问,每组询问给定两个整数 a,b,请你输出 Cbamod(109+7) 的值。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一组 a 和 b。
输出格式
共 n 行,每行输出一个询问的解。
数据范围
1≤n≤10000,
1≤b≤a≤2000
输入样例:
3
3 1
5 3
2 2输出样例:
3
10
1代码
#include <bits/stdc++.h>
using namespace std;
const int N=2010,mod=1e9+7;
int c[N][N]; //组合数
void init(){ //预处理出全部答案
for(int i=0;i<N;i++){
for(int j=0;j<=i;j++){
if(!j) c[i][j]=1; //如果j = 0,那么把c[i][j]初始化为1
else c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod; //递推式
}
}
}
int main(){
init();
int n;
cin>>n;
while(n--){
int a,b;
cin>>a>>b;
cout<<c[a][b]<<endl;
}
return 0;
}4.8.2 求组合数 II
思想
- $C_{n}^{m}=\frac{n!}{m!(n-m)!}=n!\times(m!(n-m)!)^{-1}=n!\times m!^{-1}\times (n-m)!^{-1}$
- 预处理
fact[N]和infact[N],fact[i]存储$i!$,infact[i]存储$i!^{-1}$ - 则$C_n^m=$
fact[n]*infact[m]*infact[n-m] - 预处理时利用快速幂求逆元$\pmod {1e9+7}$
模板例题 886. 求组合数 II
描述
给定 n 组询问,每组询问给定两个整数 a,b,请你输出 Cbamod(109+7) 的值。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一组 a 和 b。
输出格式
共 n 行,每行输出一个询问的解。
数据范围
1≤n≤10000,
1≤b≤a≤105
输入样例:
3
3 1
5 3
2 2输出样例:
3
10
1代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=1e5+3,mod=1e9+7;
LL fact[N],infact[N];
LL qmi(LL a,LL k,LL p){
int res=1;
while(k){
if(k&1) res=res*a%p;
a=a*a%p;
k>>=1;
}
return res;
}
int main(){
fact[0]=infact[0]=1;
for(int i=1;i<N;i++){
fact[i]=fact[i-1]*i%mod; //存储i!
infact[i]=infact[i-1]*qmi(i,mod-2,mod)%mod; //qmi(i,mod-2,mod)快速幂求逆元
}
LL n;
cin>>n;
while(n--){
LL a,b;
cin>>a>>b;
cout<<fact[a]*infact[b]%mod*infact[a-b]%mod<<endl; //计算公式
}
return 0;
}4.8.3 求组合数 III
思想
-
卢卡斯定理:\[C_n^m\equiv C_{\frac{n}{p}}^{\frac{m}p}\times C_{n~mod~p}^{m~mod~p}\pmod p\]
-
\[
\begin{aligned}
证明:\\
&n=n_0p^0+n_1p^1+\dots+n_{k-1}p^{k-1}+n_kp^k\\
&m=m_0p^0+m_1p^1+\dots+m_{k-1}p^{k-1}+m_kp^k\\
\\
则有:\\&
\begin{aligned}
(1+x)^n&=(1+x)^{n_0p^0+n_1p^1+\dots+n_{k-1}p^{k-1}+n_kp^k}\\
&=(1+x)^{n_0p^0}\times(1+x)^{n_1p^1}\times\dots\times(1+x)^{n_{k-1}p^{k-1}}\times(1+x)^{n_kp^k}\\
&=(1+x^{p^0})^{n_0}\times(1+x^{p^1})^{n_1}\times\dots\times(1+x^{p^{k-1}})^{n_{k-1}}\times(1+x^{p^k})^{n_k}\pmod p
\end{aligned}\\
\\
&\because C_n^m在其等式左边即为x^m的系数,右边也为x^m的系数\\
又&\because m的p进制:x^m=x^{m_0p^0+m_1p^1+\dots+m_{k-1}p^{k-1}+m_kp^k}\\
&\therefore x^{m_kp^k}项在(1+x^{p^k})^{n_k}中是C_{n_k}^{m_k}x^{m_kp^k},x^{m_{k-1}p^{k-1}}项在(1+x^{p^{k-1}})^{n_{k-1}}中是C_{n_{k-1}}^{m_{k-1}}x^{m_{k-1}p^{k-1}}\\
&同理:可得C_n^m=C_{n_0}^{m_0}\times C_{n_1}^{m_1}\times\dots\times C_{n_{k-1}}^{m_{k-1}}\times C_{n_k}^{m_k}\pmod p\\
\\
&\because n,m是p进制数\\
&\therefore n_0=n~mod~p,m_0=m~mod~p\\
&此时使得n,m在p进制下右移一位,即\lfloor \frac{n}{p}\rfloor,\lfloor \frac{m}{p}\rfloor\\
&对于\lfloor \frac{n}{p}\rfloor,\lfloor \frac{m}{p}\rfloor 重复上述步骤:\\
&C_{\lfloor \frac{n}{p}\rfloor}^{\lfloor \frac{m}{p}\rfloor}\equiv C_{n_1}^{m_1}\times C_{n_2}^{m_2}\times\dots\times C_{n_{k-1}}^{m_{k-1}}\times C_{n_k}^{m_k}\pmod p\\\\
&最终得到:C_n^m=C_{\lfloor \frac{n}{p}\rfloor}^{\lfloor \frac{m}{p}\rfloor}\times C_{n~mod~p}^{m~mod~p}\pmod p
\end{aligned}
\]
模板例题
描述
给定 n 组询问,每组询问给定三个整数 a,b,p,其中 p 是质数,请你输出 Cbamodp 的值。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一组 a,b,p。
输出格式
共 n 行,每行输出一个询问的解。
数据范围
1≤n≤20,
1≤b≤a≤1018,
1≤p≤105,
输入样例:
3
5 3 7
3 1 5
6 4 13输出样例:
3
3
2代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL qmi(LL a,LL k,LL p){
LL res=1;
while(k){
if(k&1) res=res*a%p;
a=a*a%p;
k>>=1;
}
return res;
}
LL C(LL a,LL b,LL p){
if(b>a) return 0;
LL res=1;
for(LL i=1,j=a;i<=b;i++,j--){
res=res*j%p;
res=res*qmi(i,p-2,p)%p;
}
return res;
}
LL lucas(LL a,LL b,LL p){
if(a<p&&b<p) return C(a,b,p);
return C(a%p,b%p,p)*lucas(a/p,b/p,p)%p;
}
int main(){
int n;
cin>>n;
while(n--){
LL a,b;
LL p;
cin>>a>>b>>p;
cout<<lucas(a,b,p)<<endl;
}
return 0;
}4.8.4 求组合数 IV
思想
- 利用高精度存储所有的方案数
模板例题 888. 求组合数 IV
描述
输入 a,b,求 Cba 的值。
注意结果可能很大,需要使用高精度计算。
输入格式
共一行,包含两个整数 a 和 b。
输出格式
共一行,输出 Cba 的值。
数据范围
1≤b≤a≤5000
5 3输出样例:
输出样例:
10代码
#include <bits/stdc++.h>
using namespace std;
const int N=5010;
int primes[N];
int sum[N];
bool vis[N];
int cnt;
void get_primes(int n){
for(int i=2;i<=n;i++){
if(!vis[i]) primes[cnt++]=i;
for(int j=0;primes[j]<=n/i;j++){
vis[primes[j]*i]=1;
if(i%primes[j]==0) break;
}
}
}
int get(int n,int p){
int res=0;
while(n){
res+=n/p;
n/=p;
}
return res;
}
vector<int> mul(vector<int> a,int b){
vector<int> c;
int t=0;
for(int i=0;i<a.size();i++){
t+=a[i]*b;
c.push_back(t%10);
t/=10;
}
while(t){
c.push_back(t%10);
t/=10;
}
return c;
}
int main(){
int a,b;
cin>>a>>b;
get_primes(a);
for(int i=0;i<cnt;i++){
int p=primes[i];
sum[i]=get(a,p)-get(a-b,p)-get(b,p);
}
vector<int> res;
res.push_back(1);
for(int i=0;i<cnt;i++){
for(int j=0;j<sum[i];j++){
res=mul(res,primes[i]);
}
}
for(int i=res.size()-1;i>=0;i--) cout<<res[i];
return 0;
}4.9 容斥原理
思想
-
-
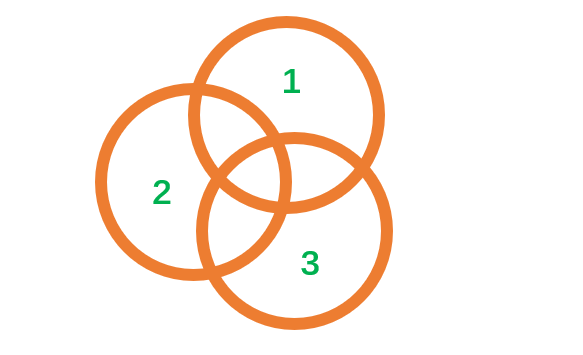
求\[S=S_1\cup S_2\cup S_3\]的面积:
\[
\begin{aligned}
由图可知:S=&S_1\cup S_2\cup S_3\\
=&S_1+S_2+S_3\\
&-S_1\cap S_2-S_1\cap S_3-S_2\cap S_3\\
&+S_1\cap S_2\cap S_3
\end{aligned}
\] -
推广求\[S=S_1\cup S_2\cup S_3\cap S_4\]的面积:
\[
\begin{aligned}
S=&S_1\cup S_2\cup S_3\cap S_4\\
=&S_1+S_2+S_3+S_4\\
&-S_1\cap S_2-S_1\cap S_3-S_1\cap S_4-S_2\cap S_3-S_2\cap S_4-S_3\cap S_4\\
&+S_1\cap S_2\cap S_3+S_1\cap S_2\cap S_4+S_1\cap S_3\cap S_4+S_2\cap S_3\cap S_4\\
&-S_1\cap S_2\cap S_3\cap S_4
\end{aligned}
\] -
若将面积作为集合看待,则容易推出:
\[
\begin{aligned}
&设U中元素有n种不同的属性,而第i种属性称为P_i拥有属性P_i的元素构成集合S_i,那么\\\\
&\begin{aligned}
\Bigg|\bigcup_{i=1}^{n}S_i\Bigg|=&\sum_i|S_i|-\sum_{i\lt j}|S_i\cap S_j|+\sum_{i\lt j\lt k}|S_i\cap S_j\cap S_k|-\dots\\
&+(-1)^{m-1}\sum_{a_i\lt a_{i+1}}\Bigg|\bigcap_{i=1}^mS_{a_i}\Bigg|+\dots+(-1)^{n-1}|S_1\cap\dots\cap S_n|\\
\end{aligned}\\\\&即:\\\\&\Bigg|\bigcup_{i=1}^{n}S_i\Bigg|=\sum_{m=1}^n(-1)^{m-1}\sum_{a_i\lt a_{i+1}}\Bigg|\bigcap_{i=1}^mS_{a_i}\Bigg|
\end{aligned}
\]
模板例题 890. 能被整除的数
给定一个整数 n 和 m 个不同的质数 p1,p2,…,pm。
请你求出 1∼n 中能被 p1,p2,…,pm 中的至少一个数整除的整数有多少个。
输入格式
第一行包含整数 n 和 m。
第二行包含 m 个质数。
输出格式
输出一个整数,表示满足条件的整数的个数。
数据范围
1≤m≤16,
1≤n,pi≤109
输入样例:
10 2
2 3输出样例:
7代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=20;
int p[N];
int main(){
int n,m;
cin>>n>>m;
for(int i=0;i<m;i++) cin>>p[i];
LL res=0;
for(int i=1;i<1<<m;i++){ // 1~2^m-1这些数代表2^m-1个不同的项
LL t=1,s=0; //s代表当前枚举的项中包含集合的个数
for(int j=0;j<m;j++){ //看这个项的第 j 位是否包含,1代表包含,0代表不包含
if(i>>j&1){ //选
if(t*p[j]>n){ //此时 n/t = 0,直接break即可
t=-1;
break;
}
t*=p[j];
s++;
}
}
if(t!=-1){
if(s%2) res+=n/t; //加奇数项的个数
else res-=n/t; //减偶数项的个数
}
}
cout<<res<<endl;
return 0;
}4.10 博弈论
概念
若一个游戏满足:
- 由两名玩家交替行动
- 在游戏进行的任意时刻,可以执行的合法行动与轮到哪位玩家无关
- 不能行动的玩家判负
则称该游戏为一个公平组合游戏
尼姆游戏(NIM)属于公平组合游戏,但常见的棋类游戏,比如围棋就不是公平组合游戏,因为围棋交战双方分别只能落黑子和白子,胜负判定也比较负责,不满足条件2和3
4.10.1 Nim 游戏
游戏规则
给定n堆石子,两位玩家轮流操作,每次操作可以从任意一堆石子中拿走任意数量的石子(可以拿完,但不能不拿),最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
例如:有两堆石子,第一堆有2个,第二堆有3个,先手必胜。
操作步骤
- 先手从第二堆拿走1个,此时第一堆和第二堆数目相同
- 无论后手怎么拿,先手都在另外一堆石子中取走相同数量的石子即可
思想
- 必胜状态:先手进行某一个操作,留给后手是一个必败状态时,对于先手来说是一个必胜状态。即先手可以走到某一个必败状态
- 必败状态:先手无论如何操作,留给后手都是一个必胜状态时,对于先手来说是一个必败状态。即先手走不到任何一个必败状态
- 结论:假设有\[n\]堆石子,数目分别是\[a_1,a_2,\dots,a_n\],如果\[a_1\oplus a_2\oplus\dots\oplus a_n\ne 0\],先手必胜;否则先手必败。
证明
-
操作到最后时,每堆石子数都是\[0\],即:$0\oplus 0\oplus\dots\oplus0=0$
-
在操作过程中,如果$a_1\oplus a_2\oplus\dots\oplus a_n=x\ne 0$,那么玩家必然可以通过拿走某一堆若干个石子将异或结果变为$0$
\[
\begin{aligned}
证明:&\\
&设x的二进制表示中最高一位1在第k位\\
&则a_1,a_2,\dots,a_n中,必然有一个数a_i,它的第k为1\\
&且一定满足:a_i\oplus x\lt a_i\\
&若从第i堆石子中拿走(a_i−a_i\oplus x)个石子\\
&则第i石子还剩a_i−(a_i−a_i\oplus x)==a_i\oplus x个石子\\
&由:a_1\oplus a_2\oplus\dots\oplus a_i \oplus\dots a_n=x\ne 0可知\\
&此时:a_1\oplus a_2\oplus\dots\oplus a_i\oplus x \oplus\dots a_n=x\oplus x=0
\end{aligned}
\] -
在操作过程中,如果$a_1\oplus a_2\oplus\dots\oplus a_n=x=0$,那么无论玩家怎么拿,必然会导致最终异或结果不为$0$
\[
\begin{aligned}
反证明:&\\
&假设玩家从第i堆石子拿走若干个,结果仍是0\\
&不妨设拿走后,第i堆还剩下a'个石子,且a'\lt a_i\\
&此时仍有:a_1\oplus a_2\oplus\dots\oplus a'\oplus\dots a_n=0\\
&则有(a_1\oplus a_2\oplus\dots\oplus a'\oplus\dots a_n)=(a_1\oplus a_2\oplus\dots\oplus a_i\oplus\dots a_n)=a'\oplus a_i=0\\
&即:a'=a_i,与原假设a'\lt a_i矛盾\\
&故假设不成立
\end{aligned}
\] -
综上:若先手面对的局面是$a_1\oplus a_2\oplus\dots\oplus a_n\ne 0$,则先手必胜,反之先手必败
模板例题 891. Nim游戏
描述
给定 n 堆石子,两位玩家轮流操作,每次操作可以从任意一堆石子中拿走任意数量的石子(可以拿完,但不能不拿),最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
输入格式
第一行包含整数 n。
第二行包含 n 个数字,其中第 i 个数字表示第 i 堆石子的数量。
输出格式
如果先手方必胜,则输出 Yes。
否则,输出 No。
数据范围
1≤n≤105,
1≤每堆石子数≤109
输入样例:
2
2 3输出样例:
Yes代码
#include <bits/stdc++.h>
using namespace std;
int main(){
int n;
cin>>n;
int res;
cin>>res;
for(int i=0;i<n-1;i++){
int m;
cin>>m;
res^=m;
}
if(res) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
return 0;
}4.10.2 台阶-Nim 游戏
描述
现在,有一个 n 级台阶的楼梯,每级台阶上都有若干个石子,其中第 i 级台阶上有 ai 个石子(i≥1)。
两位玩家轮流操作,每次操作可以从任意一级台阶上拿若干个石子放到下一级台阶中(不能不拿)。
已经拿到地面上的石子不能再拿,最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
输入格式
第一行包含整数 n。
第二行包含 n 个整数,其中第 i 个整数表示第 i 级台阶上的石子数 ai。
输出格式
如果先手方必胜,则输出 Yes。
否则,输出 No。
数据范围
1≤n≤105,
1≤ai≤109
输入样例:
3
2 1 3输出样例:
Yes分析
- 在采取最优策略的情况下,一方玩家对于偶数级台阶的操作的影响,可以被另一方玩家做相同操作的结果消去
- 故只考虑奇数级台阶的情况,适用于经典
Nim游戏 - 即:对于奇数级台阶,若先手面对的局面是$a_1\oplus a_3\oplus\dots\oplus a_n\ne 0$,则先手必胜,反之先手必败
代码
#include <bits/stdc++.h>
using namespace std;
int main(){
int n;
cin>>n;
int res;
cin>>res;
for(int i=2;i<=n;i++){
int m;
cin>>m;
if(i%2) res^=m;
}
if(res) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
return 0;
}4.10.3 集合-Nim 游戏
游戏规则
给定n堆石子以及一个由k个不同正整数构成的数字集合S。
现在有两位玩家轮流操作,每次操作可以从任意一堆石子中拿取石子,每次拿取的石子数量必须包含于集合S,最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
核心思想
- Mex运算:设$S$表示一个非负整数集合,定义$Mex(S)$为求出不属于集合$S$的最小自然数运算,例如:$S=\lbrace 0,1,2,4\rbrace$,则$Mes(S)=3$
- $SG$函数:在有向图游戏中,对于每个节点$x$,设从$x$出发共有$k$条有向边,分别到达节点$y_1,y_2\dots y_k$,定义$SG(x)$的后记节点$y_1,y_2\dots y_k$的$SG$函数值构成的集合在执行$Mex$运算的结果,即:$SG(x)=Mex(\lbrace SG(y_1),SG(y_2)\dots SG(y_k)\rbrace)$,特别地,整个有向图游戏$G$的$SG$函数值被定义为有向图游戏起点$s$的$SG$函数值,即 $SG(G)=SG(s)$
- $SG$函数的性质:
- 定义终点的$SG$函数值为$0$,
- $SG(i)=k,k\ne 0$,则$i$最大能到达的点的$SG$的范围为$[0,k−1)$
- 若$SG(i)=0$,说明走不到$0$
- 有向图游戏的和:若一个游戏的每个局面都可以构成一个有向图,则对于每个有向图的$SG(G_1),SG(G_2)\dots SG(G_n)$,对所有图的$SG$进行异或运算,即可得到该有向图游戏的和,且其结果满足
Nim游戏
$SG$函数图解
- 根据每一步的不同选择生成路径单一的有向图,每条不同的路径对应不同的局面(方案)
- 定义终点的$SG$函数值为$0$,倒推起点的$SG$函数值
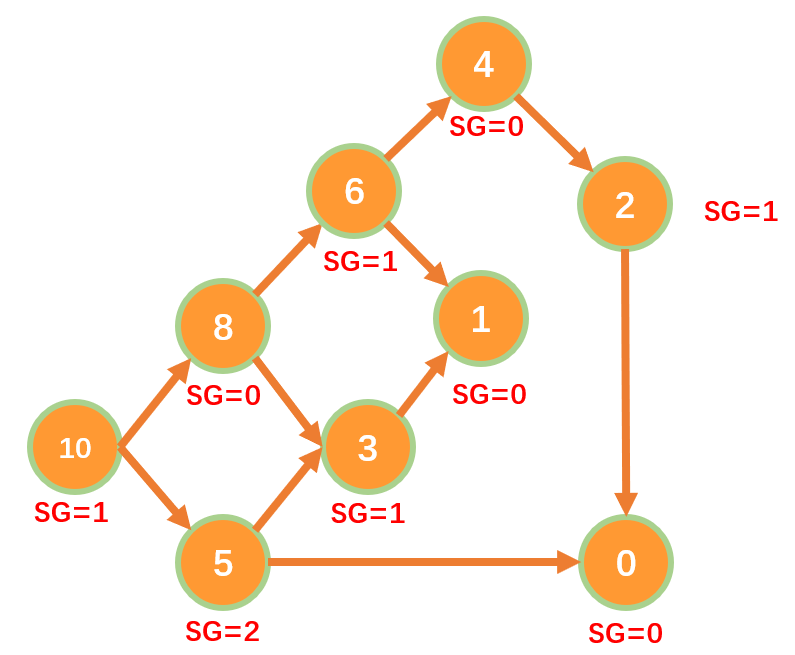
- 设一堆石子有$10$个,每次操作可取的数量为$S=\lbrace 2,5\rbrace$,无法操作即为终点,其$SG$函数如下:
证明有向图游戏的和符合Nim游戏
-
操作到最后时,每一种局面的$SG(G_i)$值都是$0$,即:$0\oplus 0\oplus\dots\oplus0=0$
-
在操作过程中,如果$SG(G_1)\oplus SG(G_2)\oplus\dots\oplus SG(G_n)=x\ne 0$,由$SG$函数的性质可知,玩家必然可以走到某一局面将异或结果变为$0$
\[
\begin{aligned}
证明:&\\
&设x的二进制表示中最高一位1在第k位\\
&则SG(G_1),SG(G_2),\dots,SG(G_n)中,必然有一个局面SG(G_i),其值的第k为1\\
&且一定满足:SG(G_i)\oplus x\lt SG(G_i)\\
&若将第i个局面的SG值取到(SG(G_i)\oplus x)\\
&由:SG(G_1)\oplus SG(G_2)\oplus\dots\oplus SG(G_i) \oplus\dots SG(G_n)=x\ne 0可知\\
&此时:SG(G_1)\oplus SG(G_2)\oplus\dots\oplus SG(G_i)\oplus x \oplus\dots SG(G_n)=x\oplus x=0
\end{aligned}
\] -
在操作过程中,如果$SG(G_1)\oplus SG(G_2)\oplus\dots\oplus SG(G_n)=x=0$,那么无论玩家如何更改局面,必然会导致最终异或结果不为$0$
\[
\begin{aligned}
反证明:&\\
&假设玩家改变第i个局面的SG值,结果仍是0\\
&不妨设SG(G_i)改变后的值为SG(G_i)',且SG(G_i)'\lt SG(G_i)\\
&此时仍有:SG(G_1)\oplus SG(G_2)\oplus\dots\oplus SG(G_i)'\oplus\dots SG(G_n)=0\\
&则有(SG(G_1)\oplus SG(G_2)\oplus\dots\oplus SG(G_i)'\oplus\dots SG(G_n))\\&=(SG(G_1)\oplus SG(G_2)\oplus\dots\oplus SG(G_i)\oplus\dots SG(G_n))=SG(G_i)'\oplus SG(G_i)=0\\
&即:SG(G_i)'=SG(G_i),与原假设SG(G_i)'\lt SG(G_i)矛盾\\
&故假设不成立
\end{aligned}
\] -
综上:若先手面对的局面是$SG(G_1)\oplus SG(G_2)\oplus\dots\oplus SG(G_n)=x\ne 0$,则先手必胜,反之先手必败,符合
Nim游戏
模板例题 893. 集合-Nim游戏
描述
给定 n 堆石子以及一个由 k 个不同正整数构成的数字集合 S。
现在有两位玩家轮流操作,每次操作可以从任意一堆石子中拿取石子,每次拿取的石子数量必须包含于集合 S,最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
输入格式
第一行包含整数 k,表示数字集合 S 中数字的个数。
第二行包含 k 个整数,其中第 i 个整数表示数字集合 S 中的第 i 个数 si。
第三行包含整数 n。
第四行包含 n 个整数,其中第 i 个整数表示第 i 堆石子的数量 hi。
输出格式
如果先手方必胜,则输出 Yes。
否则,输出 No。
数据范围
1≤n,k≤100,
1≤si,hi≤10000
输入样例:
2
2 5
3
2 4 7输出样例:
Yes代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+3;
int n,m;
int s[N],f[N]; //s存储的是可供选择的集合,f存储的是所有可能出现过的情况的sg值
int sg(int x){
if(f[x]!=-1) return f[x]; //如果存储过了,直接返回
set<int> vis; //vis代表的是当前存在的数的集合
for(int i=0;i<m;i++){
int sum=s[i];
if(x>=sum) vis.insert(sg(x-sum)); //先得到到终点的sg值后,再从后往前倒推出所有数的sg值
}
for(int i=0;;i++){
if(!vis.count(i)) return f[x]=i; //Mex操作
}
int main(){
cin>>m;
for(int i=0;i<m;i++) cin>>s[i];
cin>>n;
memset(f,-1,sizeof f);
int res=0;
for(int i=0;i<n;i++){
int x;
cin>>x;
res^=sg(x); //Nim游戏
}
if(res) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
return 0;
}4.10.4 拆分-Nim 游戏
描述
给定 n 堆石子,两位玩家轮流操作,每次操作可以取走其中的一堆石子,然后放入两堆规模更小的石子(新堆规模可以为 0,且两个新堆的石子总数可以大于取走的那堆石子数),最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
输入格式
第一行包含整数 n。
第二行包含 n 个整数,其中第 i 个整数表示第 i 堆石子的数量 ai。
输出格式
如果先手方必胜,则输出 Yes。
否则,输出 No。
数据范围
1≤n,ai≤100
输出样例:
2
2 3输出样例:
Yes分析
- 相比于
集合-Nim,这里的每一堆可以变成小于原来那堆的任意大小的两堆,即a[i]可以拆分成(b[i],b[j]) - 为了避免重复,规定
b[i]>=b[j],即:a[i]>b[i]>=b[j] - 相当于一个局面拆分成了两个局面,由$SG$函数理论,多个独立局面的$SG$值,等于这些局面$SG$值的异或和。因
- 此需要存储的状态就是
sg(b[i])^sg(b[j])
代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+3;
int n;
int f[N];
set<int> vis;
int sg(int x){
if(f[x]!=-1) return f[x];
for(int i=0;i<x;i++){
for(int j=0;j<=i;j++){ //规定j不大于i,避免重复
vis.insert(sg(i)^sg(j)); //相当于一个局面拆分成了两个局面
}
}
for(int i=0;;i++){
if(!vis.count(i)) return f[x]=i;
}
}
int main(){
cin>>n;
memset(f,-1,sizeof f);
int res=0;
for(int i=0;i<n;i++){
int x;
cin>>x;
res^=sg(x);
}
if(res) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
return 0;
}
I’m often to blogging and i really appreciate your content. The article has actually peaks my interest. I’m going to bookmark your web site and maintain checking for brand spanking new information.
This is my first time pay a quick visit at here and i am really happy to read everthing at one place
Good post! We will be linking to this particularly great post on our site. Keep up the great writing
Thanks for your supporting!
You’re so awesome! I don’t believe I have read a single thing like that before. So great to find someone with some original thoughts on this topic. Really.. thank you for starting this up. This website is something that is needed on the internet, someone with a little originality!