2022 年 CCPC 河南省赛 （A,E,F,G,H）
liyusendesu
|
ALGORITHM,Q&A
|
|
1,121
|
1

2264 字
|
28 分钟
本文最后更新于 765 天前，其中的信息可能已经有所发展或是发生改变。

A. Mocha 上小班啦

原题链接

题目大意：

  • 一个数由互不相同的 $n$ 位数组成。
  • 输出 $n$ 位的满足上述条件的最小整数（不含前导零）。
  • 不存在则输出 $-1$。

思想：

  • 签到题。
  • 当 n <= 10 时，最小的 $n$ 位数的序列为 [1, 0, 2, 3, 4, 5, 6, 7, 8 ,9]。
  • 当 n > 10 时不存在可以满足条件的数。

代码：

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <sstream>
#include <vector>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <unordered_map>
#include <unordered_set>

using namespace std;

#define IOS ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr)
#define re register
#define fi first
#define se second
#define endl '\n'

typedef long long LL;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;

const int N = 1e6 + 3;
const int INF = 0x3f3f3f3f, mod = 1e9 + 7;
const double eps = 1e-6, PI = acos(-1);

int a[] = {1, 0, 2, 3, 4, 5, 6, 7, 8, 9};

void solve(){

    int n; cin >> n;
    if(n > 10) cout << -1 << endl;  //大于10不存在满足条件的数
    else{
        for(int i = 0 ; i < n; i ++) cout << a[i];  //注意交换1和0的顺序
    }

    return ;

}

int main(){

    IOS;

    int _ = 1;

    // cin >> _;

    while(_ --){
        solve();
    }

    return 0;

}

E. Serval 的俳句

原题链接

题目大意：

  • 给定一个长度为 $n$ 的字符串 $S$。
  • 求是否存在长度为 $17$ 的子序列满足：
    • $S′_1 , S′_2 , S′_3 , S′_4 , S′_5$ 为同一个字符；
    • S′_6 , S′_7 , . . . , S′_{11}, S′_{12} 为同一个字符；
    • S′_{13}, S′_{14}, S′_{15}, S′_{16}, S′_{17} 为同一个字符。
  • 存在输出该子序列，不存在则输出 none。

思想：

  • 签到题。
  • 暴力枚举 $S_i$，统计满足的 $S'_1 \sim S'_5$，若可以找到满足的子序列，标记该字符后进入下一层循环；
  • 暴力枚举 $S_j$，统计满足的 S'_6 \sim S'_{12}，若可以找到满足的子序列，标记该字符后进入下一层循环；
  • 暴力枚举 S_k，统计满足的 S'_{13} \sim S'_{17}，若可以找到满足的子序列，则将上面标记的直接输出即可。
  • 当 n < 17 时或者没有找到存在可以满足条件的子序列，则输出 none。
  • 由于每一段的子序列很短，最坏的情况是 $26^3 \times 5^2 \times 7 = 3,075,800$，实际上的情况会远小于该时间复杂度，所以完全 $OK$。

代码：

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <sstream>
#include <vector>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <unordered_map>
#include <unordered_set>

using namespace std;

#define IOS ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr)
#define re register
#define fi first
#define se second
#define endl '\n'

typedef long long LL;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;

const int N = 200;
const int INF = 0x3f3f3f3f, mod = 1e9 + 7;
const double eps = 1e-6, PI = acos(-1);

void solve(){

    int n; cin >> n;
    if(n < 17){  //长度不够，不可能找到
        cout << "none" << endl;
        return ;
    }

    string s; cin >> s;
    int vis1[N] = {0};  //统计相同的前5个字符
    for(int i = 0; i < s.size(); i ++){
        vis1[s[i]] ++;
        if(vis1[s[i]] == 5){
            char op1 = s[i];  //标记前5个字符
            int vis2[N] = {0};  //统计相同的中间7个字符
            for(int j = i + 1; j < s.size(); j ++){
                vis2[s[j]] ++;
                if(vis2[s[j]] == 7){
                    char op2 = s[j];  //标记中间7个字符
                    int vis3[N] = {0};  //统计相同的后5个字符
                    for(int k = j + 1; k < s.size(); k ++){
                        vis3[s[k]] ++;
                        if(vis3[s[k]] == 5){  //找到最后5个字符，直接输出
                            for(int u = 0; u < 5; u ++) cout << op1;
                            for(int u = 0; u < 7; u ++) cout << op2;
                            for(int u = 0; u < 5; u ++) cout << s[k];
                            return ;
                        }
                    }
                }
            }
        }
    }
    //找不到满足条件的序列
    cout << "none" << endl; 
    return ;

}

int main(){

    IOS;

    int _ = 1;

    // cin >> _;

    while(_ --){
        solve();
    }

    return 0;

}

F. 集合之和

原题链接

题目大意：

  • 对于两个有限的数集 $A,B$，定义 $A+B$ 为：
    • $A + B = {x + y~|~ x \in A, y \in B }$
  • 记有限数集 $A$ 的元素个数为 $|A|$。
  • 给定 $n$，求满足 $|A + A| = n$ ，且满足 $\forall x \in A, 0\le x \le 5\times10^5$ 的数集 $A$。
  • 若存在 $A$ 满足上述条件，输出内含元素的数量并输出所含元素（任意解均可），不存在则输出 $-1$。

思想：

  • 思维，规律，构造。

  • 构造简单数集 $A = {0,1,2,\dots,k}, |A| = k$，则 $A + A = {0,1,2,\dots,2k},|A+A| = 2k + 1$。

  • 通过上述构造，显然当 $n$ 为奇数时一定有解，我们只需要构造满足如上规则的数集即可。

  • 接下来讨论 $n$ 为偶数的情况：

    • $|A| = 2, |A+A| = 3$，当 $n = 2$ 时无解；
    • $|A| =3,5\le |A+A|\le 6$，当 $n = 4$ 时无解；
    • 其他情况下，构造数集 $A = {0,2,3,\dots,k}$，则 $A+A ={0,2,3,\dots,2k},|A+A| = 2k$。

  • 综上所述，根据 $n$ 的奇偶性按照上述规则构造即可。

代码：

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <sstream>
#include <vector>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <unordered_map>
#include <unordered_set>

using namespace std;

#define IOS ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr)
#define re register
#define fi first
#define se second
#define endl '\n'

typedef long long LL;
typedef pair<int, string> PII;
typedef pair<LL, LL> PLL;

const int N = 1e6 + 3;
const int INF = 0x3f3f3f3f, mod = 1e9 + 7;
const double eps = 1e-6, PI = acos(-1);

int n;

void solve(){

    cin >> n;

    if(n == 2 || n == 4){
        cout << -1 << endl; 
        return ;
    }

    if(n % 2 != 0){  //奇数构造0, 1, 2, 3,...,(n - 1) / 2
        cout << (n - 1) / 2 + 1 << endl;  
        for(int i = 0; i <= (n - 1) / 2; i ++) cout << i << ' ';
    }
    else{  //偶数构造 0, 2, 3,..., n / 2
        cout << n / 2 << endl;
        cout << 0 << ' ';
        for(int i = 2; i <= n / 2; i ++) cout << i << ' ';
    }

}

int main(){

    IOS;

    int _ = 1;

    while(_ --){
        solve();
    }

    return 0;

}

G. Mocha 上大班啦

原题链接

题目大意：

  • 给定 $n$ 个 $01$ 串以及 $q$ 次操作，每次操作会把第 $i$ 个串的 $l − r$ 位替换为和第 $j$ 个串的 $l − r$ 位分别进行与运算的结果。
  • 第 $i$ 次操作有概率 $p_i$ 成功。
  • 询问最后 $n$ 个串与运算得到的串中 $1$ 的个数。

思想：

  • 思维题。
  • 概率期望套皮，其实无需处理。
  • 只要一列中出现过 $0$，由于进行的是“与”位运算，操作多少次都不会影响任何一个 $01$ 串第 $i$ 位的值，结果一定是 $0$。
  • 故直接计算初始 $01$ 串与操作后的 $1$ 的个数即为答案。

代码：

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <sstream>
#include <vector>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <unordered_map>
#include <unordered_set>

using namespace std;

#define IOS ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr)
#define re register
#define fi first
#define se second
#define endl '\n'

typedef long long LL;
typedef pair<int, string> PII;
typedef pair<LL, LL> PLL;

const int INF = 0x3f3f3f3f, mod = 1e9 + 7;
const double eps = 1e-6, PI = acos(-1);

const int N = 1010;

char a[N][4 * N];

int n, m;

void solve(){

    int res = 0;
    cin >> n >> m;
    for(int i = 0; i < n; i ++) cin >> a[i];

    int q; cin >> q;
    while(q --){
        for(int i = 0; i < 5; i ++){
            int op; cin >> op;
        }
    }

    for(int i = 0; i < m; i ++){
        int cnt = 1;
        for(int j = 0; j < n; j ++){
            if(a[j][i] == '0') cnt = 0;  //存在某一列为0时
        }
        res += cnt;
    }

    cout << res << endl;

}

int main(){

    IOS;

    int _ = 1;

    while(_ --){
        solve();
    }

    return 0;

}

H. 旋转水管

原题链接

题目大意：

  • 给定 $2 \times m$ 的水管图，水管有 I,L 两种，且两种水管均可以旋转。
  • 问是否可以通过旋转水管，使得水从 $x$ 列流入后从 $y$ 列流出。

思想：

  • DFS 搜索。
  • 水管出水状态和进入状态相关，故需要记录上一个格子流入下一个格子时的状态。
  • 分析状态可知：
    • 对于 I 形的水管，流出状态和流入状态相同。
    • 对于 L 形的水管，当流入状态是 $\uparrow$ 或 $\downarrow$ 时，流出时都有两种状态 $\leftarrow$ 和 $\rightarrow$；当流入状态是 $\leftarrow$ 或 $\rightarrow$ 时，流出时都有两种状态 $\uparrow$ 和 $\downarrow$ 。
  • 根据上述分析，我们可以得到相应状态的偏移量，在搜索时通过加上该偏移量达到坐标的转移。

代码：

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <sstream>
#include <vector>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <unordered_map>
#include <unordered_set>

using namespace std;

#define IOS ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr)
#define re register
#define fi first
#define se second
#define endl '\n'

typedef long long LL;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;

const int N = 1e6 + 10;
const int INF = 0x3f3f3f3f, mod = 1e9 + 7;
const double eps = 1e-6, PI = acos(-1);

char mp[2][N];
bool vis[2][N];

int m, sl, el;

bool flag = 0;

void dfs(int l, int r, int st){

    if(flag == 1) return ;  //满足条件直接返回

    if(l == 2 && r == el - 1){  //越界只有到达出口的情况合法
        flag = 1;  //标记答案
        return ;
    }

    if(l < 0 || l >= 2 || r < 0 || r >= m) return ;  //越界直接返回

    if(vis[l][r]) return ;  //走过该点返回

    vis[l][r] = 1;  //标记走过

    if(l >= 0 && l < 2 && r >= 0 && r < m){
        if(mp[l][r] == 'I'){  //进入状态和流出状态相同
            if(st == 0) dfs(l + 1, r, 0); 
            if(st == 1) dfs(l, r + 1, 1);
            if(st == 2) dfs(l - 1, r, 2);
            if(st == 3) dfs(l, r - 1, 3);
        }
        else{
            if(st == 0 || st == 2){  //从下面或上面流入的状态
                dfs(l, r + 1, 1);
                dfs(l, r - 1, 3);
            }
            if(st == 1 || st == 3){  //从左边或右边流入的状态
                dfs(l + 1, r, 0);
                dfs(l - 1, r, 2);
            }
        }
    }

    vis[l][r] = 0;  //搜过返回恢复现场

    return ;
}

bool solve(){
    cin >> m >> sl >> el;
    for(int i = 0; i < 2; i ++) cin >> mp[i];

    flag = 0;  //多实例，初始化
    for(int i = 0; i < 2; i ++){
        for(int j = 0; j <= m; j ++) vis[i][j] = 0;
    }

    dfs(0, sl - 1, 0);

    return flag;

}

int main(){

    IOS;

    int _ = 1;

    cin >> _;

    while(_ --){
        if(solve()) cout << "YES" << endl;
        else cout << "NO" << endl;
    }

    return 0;

}

赛后回顾与总结

生涯第一次参加 $CCPC$，先贴一张战绩：

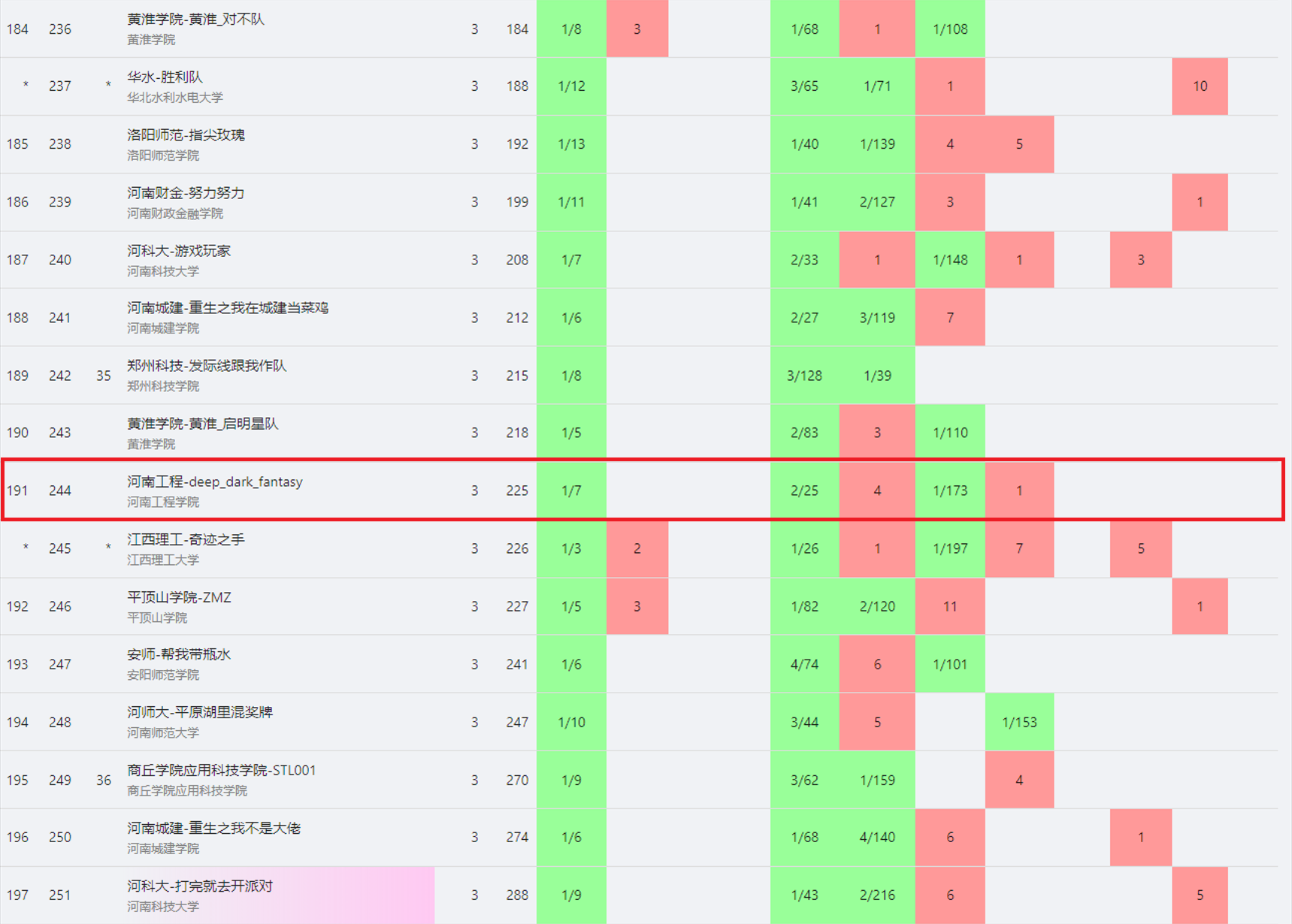
铜尾巴是 $188$，我们队伍 $191$ 喜提铁牌 （bushi） 啊吧啊吧。。。

赛程回顾

  • 两个大三的队友还是很给力的，上来就切掉了 $A$ 题，拿下了一个漂亮的 AC。
  • 我之后粗略地计算了一下 $E$ 题的时间复杂度，于是直接三个循环暴力切掉了，虽然因为统计字母数量的 vis 数组开小了，白白吃了一发 WA，为全队奠定了打铁的基础。
  • 然后我发现 $H$ 题是个搜索貌似能行？从此队伍少了一个人。。。
  • 队友开搞 $F$ ，上机打表，我在纸上手撕 $H$。
  • 队友开搞 $G$ ，最后发现是道沙笔套皮期望的诈骗题，光速写完不测样例直接冲，小 WA 一下就过了，没有一开始切掉就很可惜。
  • 然后 $zhgg$ 开始帮我调我的沙笔 $H$ 题，因为觉得 $BFS$ 的思路完全没问题，死磕到底，最后头晕脑胀坐标都搞混了，剩半小时重写一次最后都没搞出来，直接大寄 (。_。)。
  • 最后绝望看榜 $200+$ 的名次去掉打星的队伍粗略算一下能拿铜尾巴（赛后发现还是太天真），不过维他柠檬茶是真的好喝，逃。

赛后总结：

  • 打铁的根本的原因还是自己能力太弱小了。
  • 其本质就是我的懒惰，在本该出成绩的时期思想上懈怠、行动上松懈了。训练量达不到还妄想着出成绩。
  • 这次参赛也明显感受到了经验的不足，两个大三的队友异常地镇定和发挥稳定，相较而言，没有大赛经验的我在比赛时手忙脚乱拖累了团队。
  • 最后是比赛题目的分配和合作，团队协同参赛的我们互相没有磨合好，队友在讨论时我独自去切没有把握的题，最后还没有解出来，也错过了讨论和看其他题目的机会和时间。

PS：

  • 今后的计划：
    • 加训；
    • 加训；
    • 还是 TMD 加训。
  • 和队友抽空多打几场 VP，训练团队合作。
  • 卧薪尝胆，下次 $ICPC$ 必将胜利。
DFS思维构造模拟

评论

发送评论 编辑评论 


				

			

						

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
							
													

					

				

			

			
			

				

					
				

			

				

											

							
							
						

																

							
							
						

																

							
							
						

										
					
											
						

	

		
|´・ω・)ノ
ヾ(≧∇≦*)ゝ
(☆ω☆)
（╯‵□′）╯︵┴─┴
￣﹃￣
(/ω＼)
∠( ᐛ 」∠)＿
(๑•̀ㅁ•́ฅ)
→_→
୧(๑•̀⌄•́๑)૭
٩(ˊᗜˋ*)و
(ノ°ο°)ノ
(´இ皿இ｀)
⌇●﹏●⌇
(ฅ´ω`ฅ)
(╯°A°)╯︵○○○
φ(￣∇￣o)
ヾ(´･ ･｀｡)ノ"
( ง ᵒ̌皿ᵒ̌)ง⁼³₌₃
(ó﹏ò｡)
Σ(っ °Д °;)っ
( ,,´･ω･)ﾉ"(´っω･｀｡)
╮(╯▽╰)╭
o(*////▽////*)q
＞﹏＜
( ๑´•ω•) "(ㆆᴗㆆ)
😂
😀
😅
😊
🙂
🙃
😌
😍
😘
😜
😝
😏
😒
🙄
😳
😡
😔
😫
😱
😭
💩
👻
🙌
🖕
👍
👫
👬
👭
🌚
🌝
🙈
💊
😶
🙏
🍦
🍉
😣
Source: github.com/k4yt3x/flowerhd
	

	

		
颜文字
Emoji
小恐龙
花!
	


									

			

			
			
		

	






上一篇
下一篇 

                    

                    
			        推荐文章
		            

		            

							
ABC的整除问题

							
							

							
1. 基础算法初识

							
							

							
Codeforces Round #674 (Div. 3)（A~D）

							
							

							
剪绳子

							
							

							
NC14572 走出迷宫

							
							

							
3429. 全排列