本章将定制并实现更加基本,且更为常用的两类数据结构——栈与队列。与此前介绍的向向量和列表一样,它们也属于线性序列结构,故其中存放的数据对象之间也具有线性次序。相对于一般的序列结构,栈与队列的数据操作范围仅限于逻辑上的特定某端。然而,得益于其简洁性与规范性,它们既成为构建更复杂、更高级数据结构的基础,同时也是算法设计的基本出发点,甚至常常作为标准配置的基本数据结构以硬件形式直接实现。因此无论就工程或理论而言,其基础性和地位都是其它结构无法比拟的。
相对于向量和列表,栈与队列的外部接口更为简化和紧凑,故亦可视作向量与列表的特例。因此 C++ 的继承与封装机制在此可以大显身手。得益于此,本章的重点将不再拘泥于对数据结构。 内部实现机制的展示,并转而更多地从其外部特性出发,结合若干典型的实际问题介绍栈与队列的具体应用。
3.1 封装模板类
首先对于章节2,我们实现了向量和列表的模板类。本章所需实现的栈和队列的数据结构,在前者的基础上进行继承。我们将之前实现好的类模板进行封装为头文件,在之后的继承实现时,可以直接引用已经封装好的数据结构,然后提供其特有的接口。
我们以 Vector.h 的封装为例,其余的封装方法类似。
3.1.1 头文件封装
#pragma once
typedef int Rank; //定义秩
#define DEFAULT_CAPACITY 3 //默认初始容量
template <typename T> class Vector{
protected:
//基本成员
Rank _size; //元素个数
int _capacity; //实际空间
T *_elem; //元素指针
//其他内部函数
void copyFrom(T const *A, Rank lo, Rank hi); //从A中复制区间[lo, hi)
void expand(); //空间不足时扩容
void shrink(); //装填因子过小时压缩空间
public:
//构造函数
Vector(int c = DEFAULT_CAPACITY, int s = 0, T v = 0){ //默认构造
_elem = new T[_capacity = c];
for (_size = 0; _size < s; _elem[_size ++] = v);
}
//复制构造接口
Vector(T const *A, Rank n) { copyFrom(A, 0, n); } //从数组复制
Vector(T const *A, Rank lo, Rank hi) { copyFrom(A, lo, hi); } //复制数组区间
Vector(Vector<T> const &V) { copyFrom(V._elem, 0, V._size); } //拷贝构造
Vector(Vector<T> const &V, Rank lo, Rank hi) { copyFrom(V._elem, lo, hi); } //复制向量区间
//析构函数
~Vector() { delete[] _elem; } //删除数组
//其他接口函数
//只读接口
T get(Rank r); //获取秩为r的元素值
int capacity() const{ return _capacity; } //获取容量
Rank size() const { return _size; } //返回最大秩
bool empty() const { return !_size; } //判空
Rank find(T const &e, Rank lo, Rank hi) const; //无序向量区间查找
Rank find(T const &e) const { return find(e, 0, _size); } //无序向量整体查找
Rank search(T const &e, Rank lo, Rank hi) const; //有序向量区间查找
Rank search(T const &e) const { return (_size <= 0) ? -1 : search(e, 0, _size); } //有序向量整体查找
//可写入接口
T &operator[](Rank r) const; //重载[]操作符,使其能够像数组一样引用元素
Vector<T> &operator=(Vector<T> const &); //重载=操作符,使其能够向数组一样赋值
void put(Rank r, T const &e); //向量修改
void unsort() { unsort(0, _size); } //向量置乱
void unsort(Rank lo, Rank hi); //对[lo, hi)区间置乱
void reverse() { reverse(0, _size); } //向量逆序
void reverse(Rank lo, Rank hi); //对[lo, hi]区间逆序
Rank insert(Rank r, T const &e); //在秩为r的位置插入元素e
Rank insert(T const &e) { return insert(_size, e); } //默认在末尾插入元素e
int remove(Rank lo, Rank hi); //删除区间[lo,hi)的元素,并返回删除的元素个数
T remove(Rank r); //删除秩为r的元素,并返回被删除的元素值
int deduplicate(); //无序去重
int uniquify(); //有序去重
//遍历操作
void traverse(void (*)(T &)); //使用函数指针操作
template <typename VST>
void traverse(VST &); //使用函数对象操作
//排序
bool bubble(Rank lo, Rank hi); //冒泡扫描交换
void bubbleSort(Rank lo, Rank hi); //冒泡排序
void mergeSort(Rank lo,Rank hi); //归并排序
void merge(Rank lo, Rank mi, Rank hi); //二路归并
}; //Vector
//copyFrom()方法
template <typename T>
void Vector<T>::copyFrom(T const *A, Rank lo, Rank hi){
_elem = new T[_capacity = 2 * (hi - lo)]; //申请空间
_size = 0; //规模置零
while (lo < hi){
_elem[_size ++] = A[lo ++]; //逐个复制
}
}
//重载 =
template <typename T>
Vector<T> &Vector<T>::operator=(const Vector<T> &V)
{
delete[] _elem; //删除原有空间,因为下面会申请新的空间
copyFrom(V._elem, 0, V._size);
return *this; //返回值为引用便于链式赋值
}
//重载 []
template <typename T>
T &Vector<T>::operator[](Rank r) const{
return _elem[r]; //返回值为引用,这样就可以实现链式赋值(即连等)
}
//加倍扩容expend()
template <typename T>
void Vector<T>::expand(){
while (_size == _capacity){ //若实际规模等于容量
T *oldElem = _elem;
_elem = new T[_capacity <<= 1]; //申请两倍的新的空间
for (int i = 0; i < _size; i++){
_elem[i] = oldElem[i]; //若T为非基本类型,则该类型需重载=操作符
}
delete[] oldElem; //释放原空间
}
}
//缩容shrink()
template <typename T>
void Vector<T>::shrink(){
while (_size << 2 < _capacity){ //若实际规模不到容量的1/4,则缩容
T *oldElem = _elem;
_elem = new T[_capacity >>= 1]; //申请原来一半的空间
for (int i = 0; i < _size; i ++){
_elem[i] = oldElem[i]; //若T为非基本类型,则该类型需重载=操作符
}
delete[] oldElem; //释放原空间
}
}
//向量置乱
// template <typename T>
// void permute(Vector<T>& V){
// for(int i = V.size(); i > 0; i --){
// swap(V[i - 1],V[rand() % i]);
// }
// }
//封装置乱
template <typename T>
void Vector<T>::unsort(Rank lo, Rank hi){
T *V = _elem + lo; //调整指针
for (Rank i = hi - lo; i > 0; i --){
std::swap(V[i - 1], V[rand() % i]);
}
}
//封装逆序
template <typename T>
void Vector<T>::reverse(Rank lo, Rank hi){
T *V = _elem; //调整指针
Rank l = lo, r = hi - 1;
while(l < r){
std::swap(V[l],V[r]);
l ++, r--;
}
}
//顺序查找
template <typename T>
Rank Vector<T>::find(T const &e, Rank lo, Rank hi) const{
while ((lo < hi --) && (e != _elem[hi])); //当匹配到对应的e后停止,并返回秩
return hi; //若查找失败,会返回lo - 1
}
// 二分查找
template <typename T>
Rank Vector<T>::search(T const &e, Rank lo, Rank hi) const{ //在有序向量的区间[lo, hi)内查找元素e,0 <= lo <= hi <= _size
T* A = _elem;
while ( lo < hi ){ //每步迭代仅需做一次比较判断,有两个分支
Rank mi = ( lo + hi ) >> 1; //以中点为轴点
( e < A[mi] ) ? hi = mi : lo = mi + 1; //经比较后确定深入[lo, mi)或(mi, hi)
} //成功查找不能提前终止
Rank p = -- lo; //循环结束时,lo为大于e的元素的最小秩,故lo - 1即不大于e的元素的最大秩
if(A[p] == e) return p; //有多个命中元素时,总能保证返回秩最大者
return -1; //查找失败时,返回 -1
}
//获取秩为r的元素值
template <typename T>
T Vector<T>::get(Rank r){
T value = _elem[r];
return value;
}
//修改
template <typename T>
void Vector<T>::put(Rank r, T const &e){
_elem[r] = e;
}
//插入
template <typename T>
Rank Vector<T>::insert(Rank r, T const &e){ //将e作为秩为r元素插入
expand(); //若需要,先扩容
for (int i = _size; i > r;) _elem[i] = _elem[i - 1]; //整体后移一位,从后向前
_elem[r] = e, _size ++; //置入e并更新容量
return r; //返回秩
}
//区间删除
template <typename T>
int Vector<T>::remove(Rank lo, Rank hi){
if (lo == hi) return 0; //出于效率考虑,单独处理退化情况,如remove(0,0)
while(hi < _size){
_elem[lo ++] = _elem[hi ++]; //整体前移,若删除区间大于其后缀区间,未覆盖部分不做处理,下次缩容时自动消除
}
_size = lo; //确定新界限
shrink(); //若装填因子过小,缩容
return hi - lo; //返回删除元素的个数
}
//删除秩为r的元素
template <typename T>
T Vector<T>::remove(Rank r){
T re_elem = _elem[r]; //备份将被删除的元素
remove(r, r + 1); //调用区间删,等效为对区间[r, r + 1)的删除
return re_elem; //反回被删除的元素
}
//无序向量去重
template <typename T>
int Vector<T>::deduplicate(){
int oldSize = _size; //记录原始规模
Rank i = 1;
while (i < _size){ //从前向后依次检查_elem[i]
(find(_elem[i], 0, i) < 0) ? //在其前缀中寻找相同元素
i ++ : remove(i); //若查找到,删除该元素并检查其后继元素
}
return oldSize - _size; //返回删除的元素个数
}
//有序向量去重
template <typename T>
int Vector<T>::uniquify(){
int i = 0, j = 0;
while(++ j < _size){//逐一扫描,直至末元素
if(_elem[i] != _elem[j]){ //跳过雷同元素
_elem[++i ] = _elem[j];//发现不同元素时,向前移至紧邻于前者右侧
}
}
_size = ++ i; shrink();//直接截去尾部多余的元素
return j - i;
}
// 方法一:
template <typename T>
void Vector<T>::traverse(void (*visit)(T&)){ // 借助函数指针机制
for (int i = 0; i < _size; i ++){
visit(_elem[i]);
}
}
// 方法二:
template <typename T> // 元素类型
template <typename VST> // 操作器
void Vector<T>::traverse(VST& visit){ // 借助函数对象机制
for (int i = 0; i < _size; i ++){
visit(_elem[i]); // 遍历变量
}
}
template <typename T, typename VST>
void traverse(VST& visit, T& V, Rank lo, Rank hi) {
for(Rank i = lo; i <= hi; i ++){
visit(V[i]);
}
}
//冒泡扫描交换
template <typename T>
void Vector<T>::bubbleSort(Rank lo, Rank hi)
{ while (!bubble(lo,hi --)); } //逐趟做扫描交换,直至全序
//冒泡排序
template <typename T>
bool Vector<T>::bubble(Rank lo, Rank hi){
bool sorted = true; //整体有序标志
while (++ lo < hi){ //自左向右,逐一检查各对相邻元素
if (_elem[lo - 1] > _elem[lo]){ //若逆序
sorted = false;
std::swap(_elem[lo - 1], _elem[lo]); //交换
}
}
return sorted; //返回有序标志
}
//分治策略
template <typename T>
void Vector<T>::mergeSort(Rank lo, Rank hi){
if(hi - lo < 2) return;
int mi = (lo + hi) >> 1;
mergeSort(lo, mi);//对前半区间排序
mergeSort(mi, hi);//对后半区间排序
merge(lo, mi, hi);//两个区间的归并
}
//归并的实现
template <typename T>
void Vector<T>::merge(Rank lo, Rank mi, Rank hi){
T* A = _elem + lo;
int lb = mi - lo; T* B = new T[lb];
for(Rank i = 0; i < lb; i ++) B[i] = A[i];
int lc = hi - mi; T* C = _elem + mi;
for(Rank i = 0, j = 0, k = 0; (j < lb) || (k < lc);){
if((j < lb) && (!(k < lc) || (B[j] <= C[k]))) A[i ++] = B[j ++];
if((k < lc) && (!(j < lb) || (C[k] < B[j]))) A[i ++] = C[k ++];
}
delete [] B;
}注意:
-
关于
#pragma once, 是受到绝大多数现代编译器支持的非标准语用。当某个头文件中包含它时,指示编译器只对其分析一次,即使它在同一源文件中(直接或间接)被包含了多次也是如此。#pragma once // 头文件的内容 -
阻止同一头文件的多次包含的标准方式是使用包含防护:
#ifndef LIBRARY_FILENAME_H #define LIBRARY_FILENAME_H // 头文件的内容 #endif /* LIBRARY_FILENAME_H */
参考内容:实现定义的行为控制
3.1.2 头文件的位置
我们将上述代码封装完毕后,将其文件命名为 Vector.h,然后置于配置环境文件所属的 include 文件夹下,或编译时默认引用的文件路径下。
例如:D:\mingw64\x86_64-w64-mingw32\include
3.1.3 测试
#include <iostream>
#include "Vector.h"
using namespace std;
void show(int e){
cout << e << " ";
}
void test_01(){
Vector<int> a;
for(int i = 1; i <= 20; i ++){
a.insert(i);
}
a.unsort(0, a.size());
traverse(show, a, 0, a.size() - 1);
cout << endl;
a.bubbleSort(0, a.size());
for(int i = 0; i < a.size(); i ++) cout << a[i] << " ";
cout << endl;
}
int main(){
test_01();
system("pause");
return 0;
}3.2 栈
栈(stack)是存放数据对象的一种特殊容器,其中的数据元素按线性的逻辑次序排列,故也可定义首、末元素。不过,尽管栈结构也支持对象的插入和删除操作,但其操作的范围仅限于栈的某一特定端。也就是说,若约定新的元素只能从某一端插入其中,则反过来也只能从这一端删除已有的元素。禁止操作的另一端,称作盲端。
入栈与出栈:
- 栈中可操作的一端更多也称作栈顶(stack top),而另一无法直接操作的盲端则更多地称作栈底(stack bottom)。
- 作为抽象数据类型,除了引用栈顶的
top()等操作外,最常用的插入与删除操作分别称作入栈(push)和出栈(pop)。
后进先出:
- 由以上关于栈操作位置的约定和限制不难看出,栈中元素接受操作的次序必然始终遵循所谓"后进先出"(last-in-first-out,LIFO)的规律。
- 从栈结构的整个生命期来看,更晚(早) 出栈的元素应为更早(晚)入栈者;反之,更晚(早)入栈者应更早(晚)出栈。
3.2.1 接口
ADT 接口
| 操作接口 | 功能 | 返回类型 |
|---|---|---|
size() |
报告栈的规模 | int |
empty() |
判断栈是否为空 | bool |
push(e) |
将e插至栈顶 |
void |
pop() |
删除栈顶对象 | T |
top() |
引用栈顶对象 | T& |
Stack 模板类
#include "Vector.h"
template <typename T> class Stack: public Vector<T> { //将向量的首/末端作为栈底/顶
public:
//size()、empty()以及其它开放接口,均可直接沿用
void push ( T const &e ) { this -> insert ( e ); } //入栈:等效于将新元素作为向量的末元素插入
T pop() { return this -> remove ( this -> size() - 1 ); } //出栈:等效于删除向量的末元素
T &top() { return ( *this ) [this -> size() - 1]; } //取顶:直接返回向量的末元素
};3.2.2 栈的应用
递归算法所需的空间量,主要决定于最大递归深度。在达到这一深度的时刻,同时活跃的递归实例达到最多。
操作系统实现函数(递归)调用、记录调用与被调用函数(递归)实例之间的关系、实现函数(递归)调用的返回、维护同时活跃的所有函数(递归)实例等,都利用了栈的结构。
函数调用栈
在 Windows 等大部分操作系统中,每个运行中的二进制程序都配有一个调用栈(call stack)或执行栈(Cexecution stack)。借助调用栈可以跟踪属于同一程序的所有函数,记录它们之闻的相互调用关系,并保证在每一调用实例执行完毕之后,可以准确地返回。
函数调用:
- 调用栈的基本单位是顿(frame)。
- 每次函数调用时,都会相应地创建一帧,记录该函数实例在二进制程序中的返回地址(return address)以及局部变量、传入参数等,并将该帧压入调用栈。
- 若在该函数返回之前又发生新的调用,则同样地要将与新函数对应的一帧压入栈中,成为新的栈顶。
- 函数一旦运行完毕,对应的帧随即弹出,运行控制权将被交还给该函数的上层调用函数,并按照该顿中记录的返回地址确定在二进制程序中继续执行的位置。
- 调用栈中的各帧,依次对应于那些尚未返回的调用实例,亦即当时的活跃函数实例(active function instance)。
- 调用栈中各顿还需存放前一帧的起始地址,以保证其出栈之后前一顿能正确地恢复。
- 特别地,位于栈底的那帧必然对应于入口主函数
main(), 若它从调用栈中弹出,则意味着整个程序的运行结束,此后控制权将交还给操作系统。
仿照递归跟踪法,程序执行过程出现过的函数实例及其调用关系,也可构成一棵树,称作该程序的运行树。任一时刻的所有活跃函数实例,在调用栈中自底到顶,对应于运行树中从根节点 到最新活跃函数实例的一条调用路径。
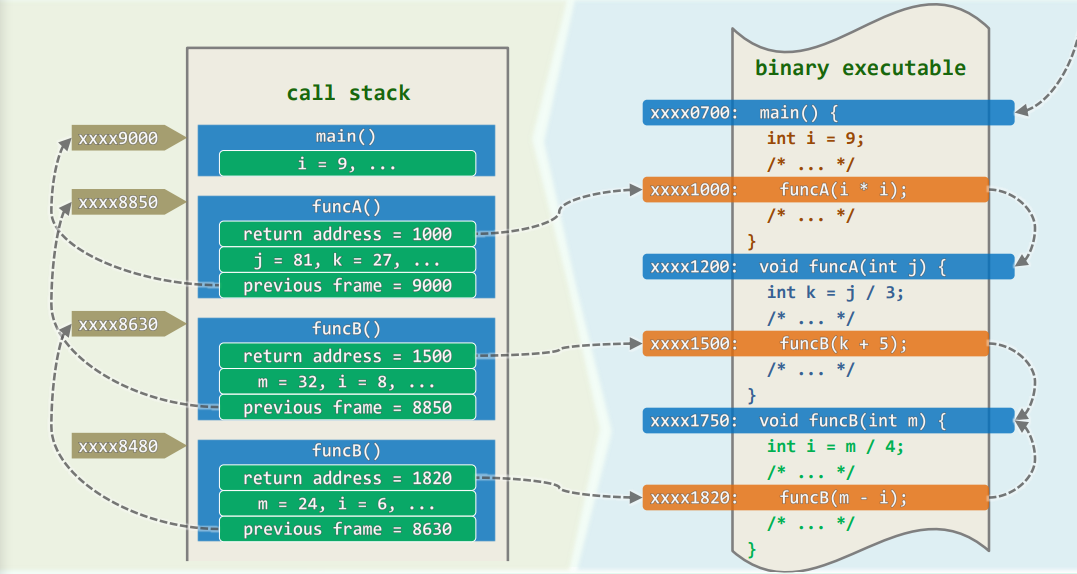
递归:
- 作为函数调用的特殊形式,递归也可借助上述调用栈得以实现。对应于上图
funcB()的自我调用,也会新压入一顿。 - 由此可见,同一函数可能同时拥有多个实例,并在调用栈中,各自占有一帧。这些帧的结构完全相同,但其中同名的参数或变量都是独立的副本。
- 比如在
funcB()的两个实例中,入口参数m和内部变量i各有一个副本。
进制转换
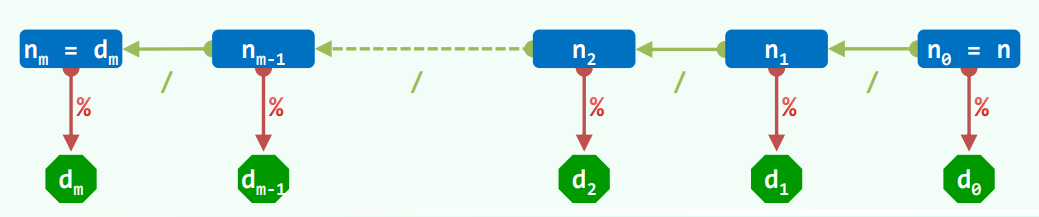
考查如下问题,任给十进制整数 n,将其转换为 X 进制的表示形式:
\[
\begin{aligned}
n
&= (d_m\dots d_2d_1d_0)_{(\lambda)}\\\\
&= d_m\times\lambda^{m}+\dots d_2\times\lambda^{2} + d_1\times\lambda^{1} + d_0\times\lambda^{0}\\\\
n_i &= (d_m\dots d_{i+1}\dots d_1)_{\lambda}\\\\
d_i &= n_i\%\lambda\\\\
n_{i+1} &= \lfloor\frac{n_i}{\lambda}\rfloor
\end{aligned}
\]
void convert ( Stack<char> &S, __int64 n, int base ) { //十进制数n到base进制的转换(迭代版)
static char digit[] //0 < n, 1 < base <= 16,新进制下的数位符号,可视base取值范围适当扩充
= { '0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'A', 'B', 'C', 'D', 'E', 'F' };
while (n > 0){ //由低到高,逐一计算出新进制下的各数位
int remainder = (int)(n % base);
S.push (digit[remainder]); //余数(当前位)入栈
n /= base; //n更新为其对base的除商
}
} //新进制下由高到低的各数位,自顶而下保存于栈S括号匹配
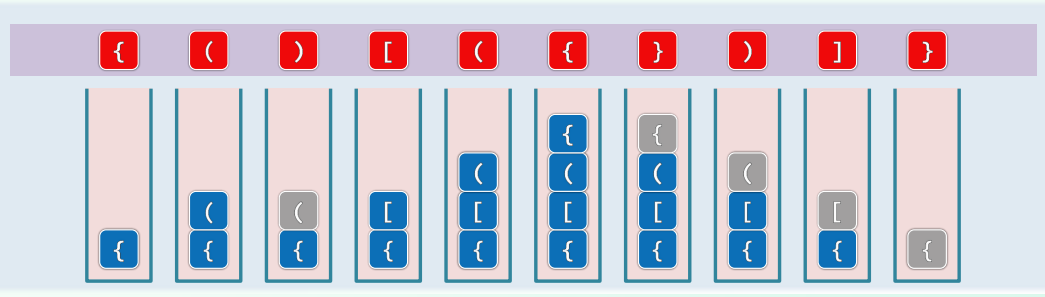
考查如下问题,给定只含有括号的表达式,判断该括号序列是否合法匹配:
bool paren(const char s[], int l, int r){ //适用四种不同括号的匹配
Stack<int> res;
for(int i = l; i < r; i ++){
char op = s[i];
if(op == '<' || op == '(' || op == '[' || op == '{') res.push(op);
else{
if(!res.empty()){
if(op == '>' && res.top() == '<' || op == ')' && res.top() == '(' || op == ']' && res.top() == '[' || op == '}' && res.top() == '{') res.pop();
else break;
}
else{
res.push(op);
break;
}
}
}
return res.empty();
}解释:
- 只要将
push()、pop()操作分别与左、右括号相对应,则长度为n的栈混洗,必然与由n对括号组成的合法表达式彼此对应 。 - 按照这一理解,借助栈结构,只需扫描一趟表达式,即可在线性时间内,判定其中的括号是否匹配。
表达式求值
针对这一类问题,运算时要考虑运算符优先级问题,则要把优先级高的数据先处理,故选择栈的结构。
提供针对包含加减乘除及括号的正整数的中缀表达式运算:
//运算符优先级比较
bool pri_cmp(const char a, const char b){
if(a == '*' || a == '/') return true;
else if((a == '+' || a == '-') && (b == '+' || b == '-')) return true;
else return false;
}
//计算子表达式的值
void eval(Stack<int> &num, Stack<char> &op){
int b = num.pop(), a = num.pop();
char c = op.pop();
int x;
if (c == '+') x = a + b;
else if (c == '-') x = a - b;
else if (c == '*') x = a * b;
else x = a / b;
num.push(x);
}
int calculate(const char str[], int n){
Stack<int> num;
Stack<char> op;
for (int i = 0; i < n; i ++){
auto c = str[i];
if(isdigit(c)){
int x = 0, j = i;
while (j < n && isdigit(str[j]))
x = x * 10 + str[j ++ ] - '0';
i = j - 1; //由于每轮循环有i++,我们需要倒指向最后一个数字
num.push(x);
}
else if(c == '(') op.push(c); //标记括号内的数据
else if(c == ')'){ //括号的优先级,先算括号
while (op.top() != '(') eval(num, op);
op.pop(); //弹括号
}
else{
while (op.size() && op.top() != '(' && pri_cmp(op.top(), c)) eval(num, op);
op.push(c); //压入新运算符
}
}
while (op.size()) eval(num, op); //清理低优先级操作
return num.pop();
}解释:
- 该算法自左向右扫描表达式,并对其中字符逐一做相应的处理。
- 利用双栈,一个操作数栈
num,一个运算符栈op。 - 按照运算符优先级运算,将栈顶运算符和即将入栈的运算符的优先级比较:
- 如果栈顶的运算符优先级低,新运算符直接入栈。
- 如果栈顶的运算符优先级高,先出栈计算子表达式,新运算符再入栈。
-
括号分为两个运算符
(和):- 遇到
(说明之后的运算要先行计算,故只需将(压栈。 - 遇到
)说明括号内的子表达式需要计算,故要逆向计算运算符直至遇到(。
- 遇到
整个计算过程只需扫描一遍表达式,时间复杂度为 $\mathcal{O}(n)$。
3.1.3 栈测试
#include <iostream>
#include "Vector.h"
using namespace std;
template <typename T> class Stack: public Vector<T> { //将向量的首/末端作为栈底/顶
public:
//size()、empty()以及其它开放接口,均可直接沿用
void push ( T const &e ) { this -> insert ( e ); } //入栈:等效于将新元素作为向量的末元素插入
T pop() { return this -> remove ( this -> size() - 1 ); } //出栈:等效于删除向量的末元素
T &top() { return ( *this ) [this -> size() - 1]; } //取顶:直接返回向量的末元素
};
//进制转换
void convert ( Stack<char> &S, __int64 n, int base ) { //十进制数n到base进制的转换(迭代版)
static char digit[] //0 < n, 1 < base <= 16,新进制下的数位符号,可视base取值范围适当扩充
= { '0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'A', 'B', 'C', 'D', 'E', 'F' };
while (n > 0){ //由低到高,逐一计算出新进制下的各数位
int remainder = (int)(n % base);
S.push (digit[remainder]); //余数(当前位)入栈
n /= base; //n更新为其对base的除商
}
} //新进制下由高到低的各数位,自顶而下保存于栈S
//括号匹配
bool paren(const char s[], int l, int r){ //适用四种不同括号的匹配
Stack<int> res;
for(int i = l; i < r; i ++){
char op = s[i];
if(op == '<' || op == '(' || op == '[' || op == '{') res.push(op);
else{
if(!res.empty()){
if(op == '>' && res.top() == '<' || op == ')' && res.top() == '(' || op == ']' && res.top() == '[' || op == '}' && res.top() == '{') res.pop();
else break;
}
else{
res.push(op);
break;
}
}
}
return res.empty();
}
//运算符优先级比较
bool pri_cmp(const char a, const char b){
if(a == '*' || a == '/') return true;
else if((a == '+' || a == '-') && (b == '+' || b == '-')) return true;
else return false;
}
//计算子表达式的值
void eval(Stack<int> &num, Stack<char> &op){
int b = num.pop(), a = num.pop();
char c = op.pop();
int x;
if (c == '+') x = a + b;
else if (c == '-') x = a - b;
else if (c == '*') x = a * b;
else x = a / b;
num.push(x);
}
int calculate(const char str[], int n){
Stack<int> num;
Stack<char> op;
for (int i = 0; i < n; i ++){
auto c = str[i];
if(isdigit(c)){
int x = 0, j = i;
while (j < n && isdigit(str[j]))
x = x * 10 + str[j ++ ] - '0';
i = j - 1; //由于每轮循环有i++,我们需要倒指向最后一个数字
num.push(x);
}
else if(c == '(') op.push(c); //标记括号内的数据
else if(c == ')'){ //括号的优先级,先算括号
while (op.top() != '(') eval(num, op);
op.pop(); //弹括号
}
else{
while (op.size() && op.top() != '(' && pri_cmp(op.top(), c)) eval(num, op);
op.push(c); //压入新运算符
}
}
while (op.size()) eval(num, op); //清理低优先级操作
return num.pop();
}
void test_01(){
Stack<int> a;
Stack<char> b;
Stack<double> c;
for(int i = 1; i <= 10; i ++){
a.push(i);
}
cout << "栈的大小为:" << a.size() << endl;
cout << "当前栈顶元素为:" << a.top() << endl;
for(int i = 0; i < 3; i ++) a.pop();
cout << "弹出3次当前栈顶元素后的栈顶元素为:" << a.top() << endl;
if(a.empty()) cout << "栈a为空" << endl;
else cout << "栈a不为空" << endl;
}
void test_02(){
Stack<char> a;
int n, X;
cout << "输入十进制数n和要转换的目标进制:" << endl;
cin >> n >> X;
convert(a, n, X);
while(!a.empty()){
cout << a.top();
a.pop();
}
cout << endl;
}
void test_03(){
cout << "输入括号序列的长度和该括号序列:" << endl;
char a[1010];
int n;
cin >> n >> a;
if(paren(a, 0, n)) cout << "匹配" << endl;
else cout << "不匹配" << endl;
}
void test_04(){
cout << "输入表达式的长度和该表达式:" << endl;
int n;
char a[1010];
cin >> n >> a;
cout << calculate(a, n) << endl;
}
int main(){
test_01(); //测试栈
test_02(); //测试进制转换 样例:12345 8
test_03(); //测试括号匹配 样例: 6 ()()()
test_04(); //测试表达式求值 样例: 11 (2+2)*(1+1)
system("pause");
return 0;
}3.3 队列
与栈一样,队列(queue)也是存放数据对象的一种容器,其中的数据对象也按线性的逻辑次序排列。
入队与出队:
- 队列结构同样支持对象的插入和删除,但两种操作的范围分别被限制于队列的两端。 允许取出元素的一端称作队头(front),而允许插入元素的另一端称作队尾(rear)。
- 队列元素的插入与删除也是修改队列结构的两种主要方式,站在被操作对象的角度,分别称作入队(enqueue)和出队(dequeue)操作。
先进先出:
- 由以上的约定和限制不难看出,与栈结构恰好相反,队列中各对象的操作次序遵循所谓”先进先出“(first-in-first-out,FIFO)。
- 从队列结构的整个生命期来看,更早(晚)出队的元素应为更早(晚)入队者,反之,更早(晚)入队者应更早(晚)出队。
3.3.1 接口
ADT 接口
| 操作接口 | 功能 | 返回类型 |
|---|---|---|
size() |
报告队列的规模 | int |
empty() |
判断队列是否为空 | bool |
enqueue(e) |
将e插至队尾 |
void |
dequeue() |
删除队尾对象 | T |
front() |
引用队首对象 | T& |
Queue 模板类
#include "List.h"
template <typename T> class Queue: public List<T> { //队列模板类(继承List原有接口)
public: //size()、empty()以及其它开放接口均可直接沿用
void enqueue ( T const &e ) { this -> insertAsLast ( e ); } //入队:尾部插入
T dequeue() { return this -> remove ( this -> first() ); } //出队:首部删除
T &front() { return this -> first() -> data; } //队首
};3.3.2 队列的应用
循环分配器
为在客户(client)群体中共享的某一资源时一套公平且高效的分配规则必不可少,而队列结构则非常适于定义和实现这样的一套分配规则。 具体地,可以借助队列 Q 实现一个资源循环分配器:
RoundRobin { //非完整结构代码,仅作为流程示例
Queue Q(clients); //参与分配资源的客户队列
while(!ServiceClosed()){ //服务有效时
e = Q.dequeue(); //队首客户出队
server(e); //分配给队首客户
Q.enqueue(e); //重新入队
}
}解释:
- 在以上所谓轮值(round robin)算法中,首先令所有参与资源分配的客户组成一个队列
Q。 - 接下来是一个反复轮回式的调度过程:
- 取出当前位于队头的客户,将资源交予该客户使用。
- 在经过固定的时间之后,回收资源,并令该客户重新入队。
- 得益于队列"先进先出"的特性,如此既可在所有客户之间达成一种均衡的公平,也可使得资源得以充分利用。
3.4 扩展应用
- 深度优先搜索基于栈的数据结构实现。
- 宽度优先搜索基于队列的数据结构实现。
- 以上对于栈和队列的扩展应用参见DFS&BFS,不再重复赘述。