数据结构：线性表——2.2 列表

本文最后更新于 976 天前，其中的信息可能已经有所发展或是发生改变。

2.2 列表

2.2.1 从向量到列表

不同数据结构内部的存储与组织方式各异，其操作接口的使用方式及时空性能也不尽相同。引入列表结构的目的在于弥补向量结构在解决某些应用问题时，在功能及性能方面的不足。二者之间的差异，表面上体现于对外的操作方式，但根源则在于其内部存储方式的不同。

从静态到动态：

数据结构支持的操作，通常无非静态和动态两类：前者仅从中获取信息，后者则会修改数据结构的局部甚至整体。以基于数组实现的向量结构为例，其 size() 和 get() 等静态操作均可在常数时间内完成，而 insert() 和 remove() 等动态操作却都可能需要线性时间。究其原因，在于"各元素物理地址连续"的约定，此即所谓的"静态存储"策略。

基于上述策略，可在 $\mathcal{O}(1)$ 的时间内由秩确定向量元素的物理地址，但反过来，在添加（删除）元素之前（之后），又不得不移动 $\mathcal{O}(n)$ 个后继元素。可见,尽管如此可使静态操作的效率达到极致，但就动态操作而言，局部的修改可能引起大范围甚至整个数据结构的调整。

列表（list）结构尽管也要求各元素在逻辑上具有线性次序，但对其物理地址却未作任何限制。此即所谓"动态存储"策略。链表（linked list）就是一种典型的动态存储结构。其中的数据，分散为一系列称作节点（node）的单位，节点之间通过指针相互索引和访问。为了引入新节点或删除原有节点, 只需在局部调整少量相关节点之间的指针。这就意味着，采用动态存储策略，至少可以大大降低动态操作的成本。

从秩到位置：

改用以上动态存储策略之后，在提高动态操作效率的同时，却又不得不舍弃原静态存储策略中循秩访问的方式，从而造成静态操作性能的下降。

以采用动态存储策略的链表为例。尽管按照逻辑次序，每个数据元素依然具有秩这一指标，但为了访问秩为 r 的元素，我们只能顺着相邻元素之间的指针，从某一端出发。逐个扫描各元素，经过 r 步选代后才能确定该元素的物理存储位置。这意味着，原先只需 $\mathcal{O}(1)$ 时间的静态操作，此时的复杂度也将线性正比于被访问元素的秩。在最坏情况下等于元素总数 $n$ ，即便在各元素被访问概率相等的情况下，平均而言也需要 $\mathcal{O}(n)$ 时间。

对数据结构的访问方式，应与其存储策略相一致。此时，既然继续延用循秩访问的方式已非上策，就应更多地习惯于通过位置，来指代并访问动态存储结构中的数据元素。

与向量中秩的地位与功能类似，列表中的位置也是指代各数据元素的一个标识性指标，借助它可以得到元素的物理存储地址。各元素的位置，通常可表示和实现为联接于元素之间的指针或引用。因此，基于此类结构设计算法时，应更多地借助逻辑上相邻元素之间的位置索引，以实现对目标元素的快速定位和访问，并进而提高算法的整体效率。

列表：

与向量一样，列表也是由具有线性逻辑次序的一组元素构成的集合。列表是链表结构的一般化推广，其中的元素称作节点（node），分别由特定的位置或链接指代。与向量一样，在元素之间也可定义前驱、直接前驱，以及后继、直接后继等关系。相对于任意元素，也有定义对应的前缀、后缀等子集。

2.2.2 接口

ADT 接口

ListNode 模板类

 #include <iostream>
#include <cstdlib>
using namespace std;
 
typedef int Rank; //秩
#define ListNodePosi(T) ListNode<T>* //列表节点位置
 
template<typename T>
struct ListNode{  //列表节点模板类（以双向链表形式实现）
    // 成员
    T data;                //数值
    ListNodePosi(T) pred;  //前驱
    ListNodePosi(T) succ;  //后继
    // 构造函数
    ListNode(){}//针对header和trailer的构造
    ListNode(T e,ListNodePosi(T) p = NULL,ListNodePosi(T) s = NULL)
        :data(e),pred(p),succ(s){}//默认构造器
    // 操作接口
    ListNodePosi(T) insertAsPred(T const &e);//紧靠当前节点之前插入新节点
    ListNodePosi(T) insertAsSucc(T const &e);//紧随当前节点之后插入新节点
};

每个节点都存有数据对象 data。为保证叙述简洁，在不致歧义的前担下，将不再区分节点及其对应的 data 对象。此外，每个节点还设有指针 pred 和 succ，分别指向其前驱和后继。为了创建一个列表节点对象，只需根据所提供的参数，分别设置节点内部的各个变量。其中前驱、后继节点的位置指针若未子指定，则默认取作 NULL。

List 模板类

 template <typename T> class List{
private:
    //数据成员
    int _size;               //规模
    ListNodePosi(T) header;  //头哨兵
    ListNodePosi(T) trailer; //尾哨兵
    //头、首、末、尾节点的秩，可分别理解为-1、0、n-1、n
 
protected:
    //内部函数
    void init();   //列表创建时的初始化
    void copyNodes ( ListNodePosi(T) p, int n );  //复制列表中自p起始的n项
    void merge (ListNodePosi(T) p, int mid, int n);   //内置归并
 
public:
    //构造函数
    List() { init(); }  //默认构造
    List ( List<T> const& L);                 //整体复制列表L
    List ( List<T> const& L, Rank r, int n);  //复制列表L的自r项起始的n项
    List ( ListNodePosi(T) p,int n);          //复制列表中自p起始的n项
 
    //析构函数
    ~List();
 
    //其他接口函数
 
    //只读函数
    Rank size() const { return _size; }    //规模
    bool empty() const { return !_size; }  //判空
    T &operator[](Rank r) const;  //重载[]，支持寻秩访问，效率低
    ListNodePosi(T) first() const { return header -> succ; }  //首节点位置
    ListNodePosi(T) last() const {return trailer -> pred; }   //尾节点位置
    bool valid(ListNodePosi(T) p)  //判断位置p是否合法
    { return p && (trailer != p) && (header != p); }  //将头、尾节点等同于NULL
    ListNodePosi(T) find ( T const& e) const                           
    { return find( e, _size, trailer); }                                //无序查找
    ListNodePosi(T) find( T const& e, int n, ListNodePosi(T) p) const;  //无序区间查找
    ListNodePosi(T) search( T const& e) const
    { return search( e, _size, trailer); }                                //有序查找
    ListNodePosi(T) search( T const& e, int n, ListNodePosi(T) p) const;  //有序区间查找
    ListNodePosi(T) selectMax (ListNodePosi(T) p, int n);                     //区间最大节点
    ListNodePosi(T) selectMax () {return selectMax( header -> succ, _size); }  //整体最大节点
 
    //可写入接口
    ListNodePosi(T) insertAsFirst (T const& e);               //将e当作首节点插入
    ListNodePosi(T) insertAsLast (T const& e);                //将e当作尾节点插入
    ListNodePosi(T) insertA (ListNodePosi(T) p, T const& e);  //将e当作p的后继插入
    ListNodePosi(T) insertB (ListNodePosi(T) p, T const& e);  //将e当作p的前驱插入
    void clear();  //列表清空
    T remove ( ListNodePosi(T) p );  //删除节点p
    int deduplicate();  //无序去重
    int uniquify();     //有序去重   
    void reverse();  //列表逆置
    void insertionSort (ListNodePosi(T) p, int n);    //插入排序
    void selectionSort ( ListNodePosi(T) p, int n );  //选择排序
    void mergeSort ( ListNodePosi(T)  p, int n );     //归并排序
    void mergeLists(ListNodePosi(T)  p, int n, List<T>& L, ListNodePosi(T) q, int m);               //归并两个链表
    void mergeLists( List<T> & L ) { mergeLists ( header -> succ, _size, L, L.header -> succ, L._size ); } //全列表归并
 
    //遍历
    void traverse(void (*)(T &)); //使用函数指针操作
    template <typename VST>
    void traverse(VST &); //使用函数对象操作
    template <typename VST>
    void traverse( VST &visit , ListNodePosi(T) r, ListNodePosi(T) l);
 
};  // List

2.2.3 初始化

头、尾节点

List 对象的内部组成及逻辑结构如图所示：

其中私有的头节点（header）和尾节点（trailer）始终存在，但对外并不可见。对外部可见的数据节点如果存在，则其中的第一个和最后一个节点分别称作首节点（first node）和末节点（last node）。

就内部结构而言，头节点紧邻于首节点之前，尾节点紧邻于末节点之后。这类经封装之后从外部不可见的节点，称作哨兵节点（sentinel node）。List 模板类中的 List::valid() 关于合法节点位置的判别准则可见，此处的两个哨兵节点从外部被等效地视作 NULL。设置哨兵节点之后，对于从外部可见的任一节点而言，其前驱和后继在列表内部都必然存在，故可简化算法的描述与实现。又如，为实现 first() 和 last() 操作，只需直接返回 header -> succ 或 trailer -> pred。此外更重要地，哨兵节点的引入，也使得相关算法不必再对各种边界退化情况做专门的处理，从而避免出错的可能。

默认构造

创建 List 对象时，默认构造方法将调用统一初始化过程 init()，在列表内部创建一对头、尾哨兵节点，并适当地设置其前驱、后继指针构成一个双向链表。

 //列表初始化，在创建列表对象时统一调用
template<typename T>
void List<T>::init(){
    header = new ListNode<T>;   //创建头哨兵节点
    trailer = new ListNode<T>;  //创建尾哨兵节点
    header -> succ = trailer; header -> pred = NULL; 
    trailer -> pred = header; trailer -> succ = NULL;
    _size = 0;  //记录规模
}

解释：

如图，该链表对外的有效部分初始为空，哨兵节点对外不可见，此后引入新的节点，都将陆续插入到这一对哨兵节点中。

在列表的其它构造方法中，内部变量的初始化过程与此相同，因此都可统一调用 init() 过程。该过程仅涉及常数次基本操作，共需运行常数时间。

由秩到位置的转换

鉴于偶尔可能需要通过秩来指定列表节点，可通过重载操作符 [] 提供一个转换接口：

 //重载下标操作符，以通过秩直接访问列表节点（虽方便，效率低，需慎用）
template <typename T>
T& List<T>::operator[] ( Rank r ) const{   //assert: 0 <= r < size
    ListNodePosi(T) p = first(); //从首节点出发
    while ( 0 < r-- ) p = p -> succ; //顺数第r个节点即是
    return p -> data; //目标节点，返回其中所存元素
}

解释：

为将任意指定的秩 r 转换为列表中对应的元素，可从首节点出发，顺着后继指针前进 r 步。

只要秩 r 合法, 该算法的正确性即一目了然。其中每步选代仅需常数时间，故该算法的总体运行时间应为 $\mathcal{O}(r + 1)$ ，线性正比于目标节点的秩。相对于向量同类接口的 $\mathcal{O}(1)$ 复杂度，列表的这一效率十分低下。

2.2.4 查找

无序列表的顺序查找

列表 ADT 针对整体和区间查找，重载了操作接口 find(e) 和 find(e，p，n)。其中，前者作为特例，可以直接调用后者。因此，只需实现后一接口：

 //无序区间查找
//在无序列表内节点p（可能是trailer）的n个（真）前驱中，找到等于e的最后者
template <typename T> 
ListNodePosi(T) List<T>::find ( T const &e, int n, ListNodePosi(T) p ) const {
    while (0 < n--) //（0 <= n <= rank(p) < _size）对于p的最近的n个前驱，从右向左
        if (e == (p = p -> pred) -> data) return p; //逐个比对，直至命中或范围越界
    return NULL; //p越出左边界意味着区间内不含e，查找失败
} //失败时，返回NULL

以上算法的思路及过程，与无序向量的顺序查找算法 Vector : :find() 相仿，故时间复杂度也应是 $\mathcal{O}(n)$ ，线性正比于查找区间的宽度。

有序列表的顺序查找

与有序向量可以借助二分查找不同，尽管有序列表中的节点已经在逻辑上单调。但本质上，其动态的存储策略，使得节点的物理地址与其逻辑次序无关，故无法进行有效的查询。

 //有序区间查找
//在有序列表内节点p（可能是trailer）的n个（真）前驱中，找到等于e的最后者
template <typename T> 
ListNodePosi(T) List<T>::search ( T const &e, int n, ListNodePosi(T) p ) const {
    while (0 < n--) //（0 <= n <= rank(p) < _size）对于p的最近的n个前驱，从右向左
        if (((p = p -> pred) -> data) <= e) break;  //直接找到，或越界
    return p;
} //失败时，返回左边界的前驱，可能是header

2.2.5 插入和删除

前插入

将新元素 e 作为当前节点的前驱插至列表的过程：

 //前插入
template <typename T> //将e紧靠当前节点之前插入于当前节点所属列表（设有哨兵头节点header）
ListNodePosi(T) ListNode<T>::insertAsPred ( T const &e ){
    ListNodePosi(T) x = new ListNode ( e, pred, this ); //创建新节点
    pred -> succ = x; pred = x; //设置正向链接
    return x; //返回新节点的位置
}

解释：

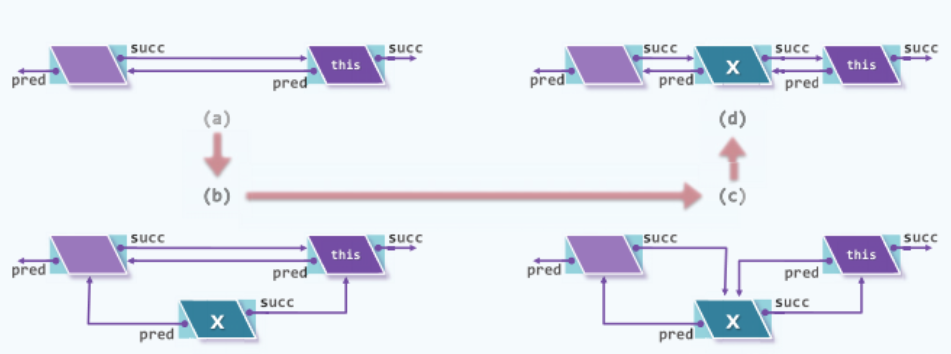
插入新节点之前, 列表局部的当前节点及其前驱如图（a）所示。
该算法首先如图（b）所示创建新节点 new，构造函数同时将其数据项置为 e，并令其后继链接 succ 指向当前节点，令其前驱链接 pred 指向当前节点的前驱节点。
随后如图（c）所示，使 new 成为当前节点前驱节点的后继，使 new 成为当前节点的前驱（次序不能颠倒）。
最终如图（d）所示，经过如此调整，新节点即被顺利地插至列表的这一局部。

注意：

列表规模记录的更新由上层调用者负责。
得益于头哨兵节点的存在，即便当前节点为列表的首节点，其前驱也如图（a）所示必然存在，故不必另做特殊处理。

后插入

将新元素 e 作为当前节点的后继插至列表的过程：

 //后插入
template <typename T> //将e紧随当前节点之后插入于当前节点所属列表（设有哨兵尾节点trailer）
ListNodePosi(T) ListNode<T>::insertAsSucc ( T const &e ){
    ListNodePosi(T) x = new ListNode ( e, this, succ ); //创建新节点
    succ -> pred = x; succ = x; //设置逆向链接
    return x; //返回新节点的位置
}

插入接口

为将节点插至列表，除了上述两种插入方法，我们可视具体要求的不同，额外提供以下大量接口：

 //e当作首节点插入
template <typename T> ListNodePosi(T) List<T>::insertAsFirst ( T const &e )
{ _size ++; return header -> insertAsSucc ( e ); } 
 
//e当作末节点插入
template <typename T> ListNodePosi(T) List<T>::insertAsLast ( T const &e )
{ _size ++; return trailer -> insertAsPred ( e ); }
 
//e当作p的后继插入（After）
template <typename T> ListNodePosi(T) List<T>::insertA ( ListNodePosi(T) p, T const &e )
{ _size ++; return p -> insertAsSucc ( e ); } 
 
//e当作p的前驱插入（Before）
template <typename T> ListNodePosi(T) List<T>::insertB ( ListNodePosi(T) p, T const &e )
{ _size ++; return p -> insertAsPred ( e ); }

删除

在列表中删除指定节点 p 的算法：

 //删除
template <typename T> 
T List<T>::remove ( ListNodePosi(T) p ){
    T e = p -> data; //备份待删除节点的数值（假定T类型可直接赋值）
    p -> pred -> succ = p -> succ; p-> succ -> pred = p -> pred; //后继、前驱
    delete p; 
    _size--; //释放节点，更新规模
    return e; //返回备份的数值
}

解释：

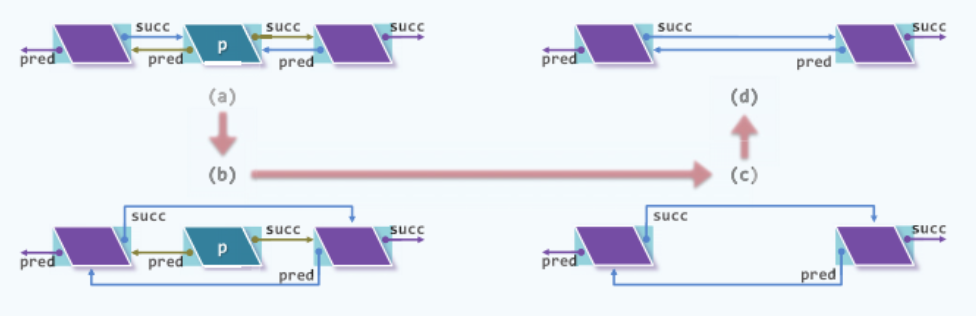
删除节点之前，列表在位置p附近的局部如图（a）所示。
为了删除位置 p 处的节点，首先如图（b）所示，令其前驱节点与后继节点相互链接。
然后如图（c）所示, 释放掉已经孤立出来的节点 p，同时相应地更新列表规模计数器 _size。
最终如图（d）所示，经过如此调整之后，原节点 p 即被顺利地从列表中摘除。

时间复杂度

由于对链表的插入和删除是直接元素插入位置的地址进行处理，故不需要像向量一样在插入或删除之后移动元素。故所有的插入和删除操作所需的时间复杂度均为 $\mathcal{O}(1)$ 。在进行频繁的插入删除操作时，列表的效率远远高于向量，可见动态存储策略的优越性。

2.2.6 复制构造和析构

copyNodes()

与向量一样，列表的内部结构也是动态创建的，故利用默认的构造方法并不能真正地完成新列表的复制创建。为此，需要专门编写相应的构造方法，通过复制某一已有列表来构造新列表。

尽管这里提供了多种形式，以允许对原列表的整体或局部复制，但其实质过程均大同小异，都可概括和转化为底层内部方法 copyNodes()。在输入参数合法的前提下，copyNodes() 首先调用 init() 方法，创建头、尾哨兵节点并做相应的初始化处理，然后自 p 所指节点起，从原列表中取出 n 个相邻的节点，并逐一作为末节点插至新列表中。

 //copyNodes()
template <typename T> //列表内部方法：复制列表中自位置p起的n项
void List<T>::copyNodes ( ListNodePosi(T) p, int n ){   //p合法，且至少有n-1个真后继节点
    init(); //创建头、尾哨兵节点并做初始化
    while ( n-- ) { insertAsLast ( p -> data ); p = p -> succ; } //将起自p的n项依次作为末节点插入
}

根据此前的分析，init() 操作以及各步适代中的插入操作均只需常数时间，故 copyNodes() 过程总体的运行时间应为 $\mathcal{O}(n + 1)$ ，线性正比于待复制列表区间的长度 n。

基于复制的构造

基于 copyNodes() 我们可以实现多种接口：

 //复制列表中自位置p起的n项（assert: p为合法位置，且至少有n-1个后继节点）
template <typename T> 
List<T>::List ( ListNodePosi(T) p, int n ) { copyNodes ( p, n ); }
 
//整体复制列表L
template <typename T> 
List<T>::List ( List<T> const& L ) { copyNodes ( L.first(), L._size ); }
 
//复制L中自第r项起的n项（assert: r+n <= L._size）
template <typename T> 
List<T>::List ( List<T> const& L, int r, int n ) { copyNodes ( L[r], n ); }

列表的清空

 //清空列表
template <typename T> 
void List<T>::clear(){   
    int oldSize = _size;
    while ( 0 < _size ) remove ( header -> succ ); //反复删除首节点，直至列表变空
}

列表的析构

与所有对象一样，列表对象析构时，将其所占用的资源归还操作系统。

 //列表析构器
template <typename T> List<T>::~List()
{ clear(); delete header; delete trailer; }

解释：

列表的析构需首先调用 clear() 接口删除并释放所有对外部有效的节点。
然后释放内部的头、尾哨兵节点。

列表的析构与清空时间复杂度一样，均为 $\mathcal{O}(n)$ ，线性正比于列表规模。

2.2.7 去重

无序列表的唯一化

旨在剔除无序列表中重复元素的接口 deduplicate()，与算法 Vector: :deduplicate() 类似，这里也是自前向后依次处理各节点 p，一旦通过 find() 接口在 p 的前驱中查到雷同者，则随即调用 remove() 接口将其删除。

 //无序列表去重
template <typename T> 
int List<T>::deduplicate() {
    if ( _size < 2 ) return 0; //平凡列表自然无重复
    int oldSize = _size; //记录原规模
    ListNodePosi(T) p = header; Rank r = 0; //p从首节点开始
    while ( trailer != ( p = p -> succ ) ){   //依次直到末节点
        ListNodePosi(T) q = find ( p -> data, r, p ); //在p的r个（真）前驱中查找雷同者
        q ? remove ( q ) : r++; //若的确存在，则删除之；否则秩加一
    } //assert: 循环过程中的任意时刻，p的所有前驱互不相同
    return oldSize - _size; //列表规模变化量，即被删除元素总数
}

解释：

向量与列表中元素的逻辑次序一致，故二者的 deduplicate() 算法亦具有类似的不变性和单调性，故正确性均可保证。

与无序向量的去重算法一样，该算法总共需做 $\mathcal{O}(n)$ 步迭代。每一步迭代中 find() 操作所需的时间线性正比于查找区间宽度。列表节点每次 remove() 操作仅需常数时间，但迭代需要的时间为 $\mathcal{O}(n^2)$ ，故时间复杂度为 $\mathcal{O}(n^2)$ 。

有序列表的唯一化

与有序向量同理，有序列表中的雷同节点也必然在逻辑上彼此紧邻。利用这一特性，可实现重复节点删除算法。位置指针 p和q 分别指向每一对相邻的节点，若二者雷同则删除 q，否则转向下一对相令节点。如此反复迭代，直至检查过所有节点。

 //有序列表去重
template <typename T> 
int List<T>::uniquify() {
    if ( _size < 2 ) return 0; //平凡列表自然无重复
    int oldSize = _size; //记录原规模
    ListNodePosi(T) p = first(); ListNodePosi(T) q; //p为各区段起点，q为其后继
    while ( trailer != ( q = p -> succ ) ) //反复考查紧邻的节点对(p, q)
        if ( p -> data != q -> data ) p = q; //若互异，则转向下一区段
        else remove ( q ); //否则（雷同），删除后者
    return oldSize - _size; //列表规模变化量，即被删除元素总数
}

整个过程运行时间为 $\mathcal{O}(n)$ ，线性正比于列表原先的规模。

2.2.8 遍历

列表也提供支持节点批量式访问的遍历接口，与向量一样，我们在此也提供两种方式：

 //方法一：//借助函数指针机制遍历
template <typename T>  
void List<T>::traverse ( void ( *visit ) ( T & ) ){   
    for ( ListNodePosi(T) p = header -> succ; p != trailer; p = p -> succ ){ 
        visit ( p -> data );  
    }
}
 
//方法二：//借助函数对象机制遍历
template <typename T> template <typename VST> //元素类型、操作器
void List<T>::traverse ( VST &visit ){  
    for ( ListNodePosi(T) p = header -> succ; p != trailer; p = p -> succ ){
        visit ( p -> data );  
    }
}

实例：

实现遍历输出

 //遍历输出从r项开始到l项
template <typename T> template <typename VST> //元素类型、操作器
void List<T>::traverse ( VST &visit , ListNodePosi(T) r, ListNodePosi(T) l){  
    for ( ListNodePosi(T) p = r -> pred -> succ; p != l -> succ; p = p -> succ ){
        visit ( p -> data );  
    }
}
 
void show(int e){
    cout << e << " ";
}

2.2.9 逆置和排序

列表逆置

交换节点的前驱和后继的指针，并交换头尾节点：

 //列表逆置
template <typename T>
void List<T>::reverse(){
    ListNodePosi(T) p = header;
    for(; p; p = p -> pred){
        std::swap(p -> pred, p -> succ);
    }
    std::swap(header, trailer);     
}

插入排序

插入排序（insertionsort）算法适用于包括向量与列表在内的任何序列结构。

思想：

始终将整个序列视作并切分为两部分: 有序的前缀，无序的后缀。通过迭代，反复地将后缀的首元素转移至前缀中。
由此可知：在任何时刻，相对于当前节点 e = S[r]，前缀 S[0, r) 总是业已有序。

 //插入排序
template <typename T>  //对起始于位置p的n个元素排序
void List<T>::insertionSort ( ListNodePosi(T) p, int n ){   //valid(p) && rank(p) + n <= size
    for (int r = 0; r <= n; r ++){   //逐一为各节点
        insertA ( search( p -> data, r, p ), p -> data ); //查找适当的位置并插入
        p = p -> succ; remove ( p -> pred ); //转向下一节点
    }
}

解释：

算法开始时该前缀为空，不变性自然满足。
现假设如图所示前缀 S[0，r) 已经有序，接下来, 借助有序序列的查找算法，可在该前缀中定位到不大于 e 的最大元素。
于是只需将 e 从无序后组中取出，并紧邻于查找返回的位置之后插入，即可使得有序前缀的范围扩大至 S[0，r]。

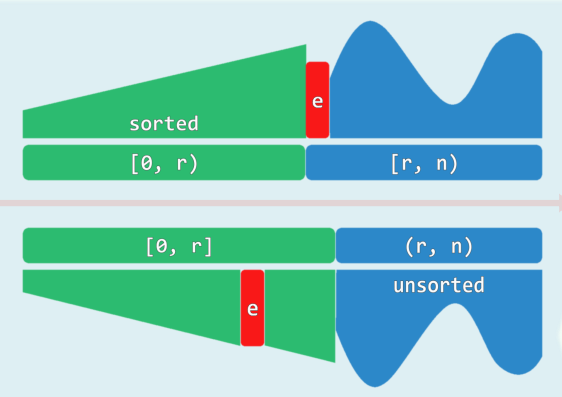
如此，该前缀的范围可不断拓展。当其最终费盖整个序列时，亦即整体有序。

插入排序算法共由 n 步迁代组成，故其运行时间应取决于各步迁代中所执行的查找、删除及插入操作的效率。根据此前的结论，插入操作和删除操作只需 $\mathcal{O}(1)$ 时间，查找操作 search() 所需时间在 $\mathcal{O}(1)$ 至 $\mathcal{O}(n)$ 之间浮动。

若输出序列完全逆序,，则各次 search() 操作所需时间将线性递增。在等概率条件下，平均仍需要 $\mathcal{O}(n^2)$ 时间。

选择排序

选择排序（selectionsort）也适用于向量与列表之类的序列结构。

思想：

与插入排序类似，该算法也将序列划分为无序前缀和有序后缀两部分，且要求要求前缀不大于后缀。
如此，每次只需从前缀中选出最大者，并作为最小元素转移至后缀中，即可使有序部分的范围不断扩张，直至整个列表有序。
由此可知：在任何时刻，后缀 S(r, n) 已经有序，且不小于前缀 S[0, r)。

首先要实现定位无序列表中最大的节点的函数 selectMax()：

 //selectMax()
template <typename T> //从起始于位置p的n个元素中选出最大者
ListNodePosi(T) List<T>::selectMax (ListNodePosi(T) p, int n){
    ListNodePosi(T) max = p; //最大者暂定为首节点p
    for ( ListNodePosi(T) cur = p; 1 < n; n-- ){ //从首节点p出发，将后续节点逐一与max比较
        if ( !lt ( ( cur = cur->succ )->data, max->data ) ) //若当前元素不小于max，则
            max = cur; //更新最大元素位置记录
    }
    return max; //返回最大节点位置
}

选择排序 selectionSort()：

 //选择排序
template <typename T> //对起始于位置p的n个元素排序
void List<T>::selectionSort ( ListNodePosi(T) p, int n ){   //valid(p) && rank(p) + n <= size
    ListNodePosi(T) head = p -> pred; ListNodePosi(T) tail = p;
    for ( int i = 0; i < n; i ++ ) tail = tail -> succ; //待排序区间为(head, tail)
    while ( 1 < n ){   //在至少还剩两个节点之前，在待排序区间内
        ListNodePosi(T) max = selectMax ( head -> succ, n ); //找出最大者（歧义时后者优先）
        insertB ( tail, remove ( max ) ); //将其移至无序区间末尾（作为有序区间新的首元素）
        tail = tail -> pred; n --;
    }
}

解释：

在算法的初始时刻，后缀为空，不变性自然满足。
如图所示，假设不变性己满足。于是，可调用无序序列的查找算法，从前绥中找出最大者 M。
接下来，只需将 M 从前绥中取出并作为首元素插入后缀，即可使得后缀的范围扩大，并继续保持有序。

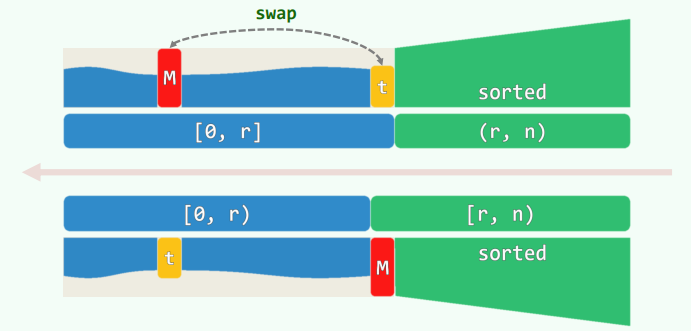
如此，该后缀的范围可不断拓展，当其最终覆盖整个序列时，亦即整体有序。

与插入排序类似地，选择排序亦由 n 步选代组成，故其运行时间取决于各步送代中查找及插入操作的效率。根据结论可知 insertB() 和 remove() 均只需 $\mathcal{O}(1)$ 时间。 selectMax() 每次必须遍历整个无序前缀，耗时应线性正比于前缀长度，全程累计耗时 $\mathcal{O}(n^2)$ 。

归并排序

基于二路归并的向量排序算法，其构思也同样适用于列表结构。实际上，有序列表的二路归并不仅可以实现，而且能够达到与有序向量二路归并同样高的效率。

仿照向量的归并排序算法 mergesort() ，采用分治策略并基于以上有序列表的二路归并算法，实现列表的归并排序算法:

 //内置归并
template <typename T>
void List<T>::merge(ListNodePosi(T) p, int mid, int n){
    int lenB = mid;
    int lenC = n - mid;
    ListNodePosi(T) A = p;
    T * B = new T[mid];
    for(int i = 0; i<mid; ++i){
        B[i]= p->data; p = p->succ;  
    }
    ListNodePosi(T) C = p;
    for(int j = 0, k = 0; j < lenB; ){
        if( lenC <= k || B[j] <= C->data ){
            A -> data = B[j ++];  
            A = A -> succ;
        }
        if( k < lenC && C -> data < B[j]){
            A -> data = C -> data;  
            A = A -> succ; C = C -> succ; 
            ++ k;
        }  
    }
    delete [] B;
}
 
//归并排序
template <typename T>
void List<T>::mergeSort(ListNodePosi(T) p, int n){
    if( n < 2 ) return ;
    ListNodePosi(T) q = p;
    int mid = n >> 1;
    int x = mid; while(x --) q = q -> succ; 
    mergeSort(p, mid); mergeSort(q, n - mid);
    if(q -> pred -> data > q -> data) merge(p, mid, n);  
}

针对两个有序的链表合并，我们提供对外接口：

 //合并两个链表
template <typename T>
void List<T>::mergeLists(ListNodePosi(T) p, int n, List<T> &L, ListNodePosi(T) q, int  m){
    List<T> t;
    while(m > 0 && n > 0){
        if(p -> data <= q -> data){
            t.insertAsLast(p -> data);
            p = p -> succ;n --;
        }
        else{
            t.insertAsLast(q -> data);
            q = q -> succ;m --;
        }
    }
    while(n > 0) t.insertAsLast(p -> data), p = p -> succ, n --;
    while(m > 0) t.insertAsLast(q -> data), q = q -> succ, m --;
    this -> clear(), L.clear();
    for(ListNodePosi(T) i = t.first(); i != t.trailer; i = i -> succ){
        this -> insertAsLast(i -> data);
    }
    p = this -> first();
}

2.2.10 列表测试

 #include <iostream>
#include <cstdlib>
using namespace std;
 
typedef int Rank; //秩
#define ListNodePosi(T) ListNode<T>* //列表节点位置
 
template<typename T>
struct ListNode{  //列表节点模板类（以双向链表形式实现）
    // 成员
    T data;                //数值
    ListNodePosi(T) pred;  //前驱
    ListNodePosi(T) succ;  //后继
    // 构造函数
    ListNode(){}//针对header和trailer的构造
    ListNode(T e,ListNodePosi(T) p = NULL,ListNodePosi(T) s = NULL)
        :data(e),pred(p),succ(s){}//默认构造器
    // 操作接口
    ListNodePosi(T) insertAsPred(T const &e);//紧靠当前节点之前插入新节点
    ListNodePosi(T) insertAsSucc(T const &e);//紧随当前节点之后插入新节点
};
 
template <typename T> class List{
private:
    //数据成员
    int _size;               //规模
    ListNodePosi(T) header;  //头哨兵
    ListNodePosi(T) trailer; //尾哨兵
    //头、首、末、尾节点的秩，可分别理解为-1、0、n-1、n
 
protected:
    //内部函数
    void init();   //列表创建时的初始化
    void copyNodes ( ListNodePosi(T) p, int n );  //复制列表中自p起始的n项
    void merge (ListNodePosi(T) p, int mid, int n);   //内置归并
 
public:
    //构造函数
    List() { init(); }  //默认构造
    List ( List<T> const& L);                 //整体复制列表L
    List ( List<T> const& L, Rank r, int n);  //复制列表L的自r项起始的n项
    List ( ListNodePosi(T) p,int n);          //复制列表中自p起始的n项
 
    //析构函数
    ~List();
 
    //其他接口函数
 
    //只读函数
    Rank size() const { return _size; }    //规模
    bool empty() const { return !_size; }  //判空
    T &operator[](Rank r) const;  //重载[]，支持寻秩访问，效率低
    ListNodePosi(T) first() const { return header -> succ; }  //首节点位置
    ListNodePosi(T) last() const {return trailer -> pred; }   //尾节点位置
    bool valid(ListNodePosi(T) p)  //判断位置p是否合法
    { return p && (trailer != p) && (header != p); }  //将头、尾节点等同于NULL
    ListNodePosi(T) find ( T const& e) const                           
    { return find( e, _size, trailer); }                                //无序查找
    ListNodePosi(T) find( T const& e, int n, ListNodePosi(T) p) const;  //无序区间查找
    ListNodePosi(T) search( T const& e) const
    { return search( e, _size, trailer); }                                //有序查找
    ListNodePosi(T) search( T const& e, int n, ListNodePosi(T) p) const;  //有序区间查找
    ListNodePosi(T) selectMax (ListNodePosi(T) p, int n);                     //区间最大节点
    ListNodePosi(T) selectMax () {return selectMax( header -> succ, _size); }  //整体最大节点
 
    //可写入接口
    ListNodePosi(T) insertAsFirst (T const& e);               //将e当作首节点插入
    ListNodePosi(T) insertAsLast (T const& e);                //将e当作尾节点插入
    ListNodePosi(T) insertA (ListNodePosi(T) p, T const& e);  //将e当作p的后继插入
    ListNodePosi(T) insertB (ListNodePosi(T) p, T const& e);  //将e当作p的前驱插入
    void clear();  //列表清空
    T remove ( ListNodePosi(T) p );  //删除节点p
    int deduplicate();  //无序去重
    int uniquify();     //有序去重   
    void reverse();  //列表逆置
    void insertionSort (ListNodePosi(T) p, int n);    //插入排序
    void selectionSort ( ListNodePosi(T) p, int n );  //选择排序
    void mergeSort ( ListNodePosi(T)  p, int n );     //归并排序
    void mergeLists(ListNodePosi(T)  p, int n, List<T>& L, ListNodePosi(T) q, int m);               //归并两个链表
    void mergeLists( List<T> & L ) { mergeLists ( header -> succ, _size, L, L.header -> succ, L._size ); } //全列表归并
 
    //遍历
    void traverse(void (*)(T &)); //使用函数指针操作
    template <typename VST>
    void traverse(VST &); //使用函数对象操作
    template <typename VST>
    void traverse( VST &visit , ListNodePosi(T) r, ListNodePosi(T) l);
 
};  // List
 
//列表初始化，在创建列表对象时统一调用
template<typename T>
void List<T>::init(){
    header = new ListNode<T>;   //创建头哨兵节点
    trailer = new ListNode<T>;  //创建尾哨兵节点
    header -> succ = trailer; header -> pred = NULL; 
    trailer -> pred = header; trailer -> succ = NULL;
    _size = 0;  //记录规模
}
 
// //重载下标操作符，以通过秩直接访问列表节点（虽方便，效率低，需慎用）
// template <typename T>
// T& List<T>::operator[] ( Rank r ) const{   //assert: 0 <= r < size
//     ListNodePosi(T) p = first(); //从首节点出发
//     while (0 < r--) p = p -> succ; //顺数第r个节点即是
//     return p -> data; //目标节点，返回其中所存元素
// }
 
//无序区间查找
//在无序列表内节点p（可能是trailer）的n个（真）前驱中，找到等于e的最后者
template <typename T> 
ListNodePosi(T) List<T>::find ( T const &e, int n, ListNodePosi(T) p ) const {
    while (0 < n--) //（0 <= n <= rank(p) < _size）对于p的最近的n个前驱，从右向左
        if (e == (p = p -> pred) -> data) return p; //逐个比对，直至命中或范围越界
    return NULL; //p越出左边界意味着区间内不含e，查找失败
} //失败时，返回NULL
 
//有序区间查找
//在有序列表内节点p（可能是trailer）的n个（真）前驱中，找到等于e的最后者
template <typename T> 
ListNodePosi(T) List<T>::search ( T const &e, int n, ListNodePosi(T) p ) const {
    while (0 < n--) //（0 <= n <= rank(p) < _size）对于p的最近的n个前驱，从右向左
        if (((p = p -> pred) -> data) <= e) break;  //直接找到，或越界
    return p;
} //失败时，返回左边界的前驱，可能是header
 
//前插入
template <typename T> //将e紧靠当前节点之前插入于当前节点所属列表（设有哨兵头节点header）
ListNodePosi(T) ListNode<T>::insertAsPred ( T const &e ){
    ListNodePosi(T) x = new ListNode ( e, pred, this ); //创建新节点
    pred -> succ = x; pred = x; //设置正向链接
    return x; //返回新节点的位置
}
 
//后插入
template <typename T> //将e紧随当前节点之后插入于当前节点所属列表（设有哨兵尾节点trailer）
ListNodePosi(T) ListNode<T>::insertAsSucc ( T const &e ){
    ListNodePosi(T) x = new ListNode ( e, this, succ ); //创建新节点
    succ -> pred = x; succ = x; //设置逆向链接
    return x; //返回新节点的位置
}
 
//e当作首节点插入
template <typename T> ListNodePosi(T) List<T>::insertAsFirst ( T const &e )
{ _size ++; return header -> insertAsSucc ( e ); } 
 
//e当作末节点插入
template <typename T> ListNodePosi(T) List<T>::insertAsLast ( T const &e )
{ _size ++; return trailer -> insertAsPred ( e ); }
 
//e当作p的后继插入（After）
template <typename T> ListNodePosi(T) List<T>::insertA ( ListNodePosi(T) p, T const &e )
{ _size ++; return p -> insertAsSucc ( e ); } 
 
//e当作p的前驱插入（Before）
template <typename T> ListNodePosi(T) List<T>::insertB ( ListNodePosi(T) p, T const &e )
{ _size ++; return p -> insertAsPred ( e ); } 
 
//删除
template <typename T> 
T List<T>::remove ( ListNodePosi(T) p ){
    T e = p -> data; //备份待删除节点的数值（假定T类型可直接赋值）
    p -> pred -> succ = p -> succ; p-> succ -> pred = p -> pred; //后继、前驱
    delete p; 
    _size--; //释放节点，更新规模
    return e; //返回备份的数值
}
 
//copyNodes()
template <typename T> //列表内部方法：复制列表中自位置p起的n项
void List<T>::copyNodes ( ListNodePosi(T) p, int n ){   //p合法，且至少有n-1个真后继节点
    init(); //创建头、尾哨兵节点并做初始化
    while ( n-- ) { insertAsLast ( p -> data ); p = p -> succ; } //将起自p的n项依次作为末节点插入
}
 
//复制列表中自位置p起的n项（assert: p为合法位置，且至少有n-1个后继节点）
template <typename T> 
List<T>::List ( ListNodePosi(T) p, int n ) { copyNodes ( p, n ); }
 
//整体复制列表L
template <typename T> 
List<T>::List ( List<T> const& L ) { copyNodes ( L.first(), L._size ); }
 
//复制L中自第r项起的n项（assert: r+n <= L._size）
template <typename T> 
List<T>::List ( List<T> const& L, int r, int n ) { copyNodes ( L[r], n ); }
 
//清空列表
template <typename T> 
void List<T>::clear(){   
    int oldSize = _size;
    while ( 0 < _size ) remove ( header -> succ ); //反复删除首节点，直至列表变空
}
 
//列表析构器
template <typename T> List<T>::~List()
{ clear(); delete header; delete trailer; }
 
//无序列表去重
template <typename T> 
int List<T>::deduplicate() {
    if ( _size < 2 ) return 0; //平凡列表自然无重复
    int oldSize = _size; //记录原规模
    ListNodePosi(T) p = header; Rank r = 0; //p从首节点开始
    while ( trailer != ( p = p -> succ ) ){   //依次直到末节点
        ListNodePosi(T) q = find ( p -> data, r, p ); //在p的r个（真）前驱中查找雷同者
        q ? remove ( q ) : r++; //若的确存在，则删除之；否则秩加一
    } //assert: 循环过程中的任意时刻，p的所有前驱互不相同
    return oldSize - _size; //列表规模变化量，即被删除元素总数
}
 
//有序列表去重
template <typename T> 
int List<T>::uniquify() {
    if ( _size < 2 ) return 0; //平凡列表自然无重复
    int oldSize = _size; //记录原规模
    ListNodePosi(T) p = first(); ListNodePosi(T) q; //p为各区段起点，q为其后继
    while ( trailer != ( q = p -> succ ) ) //反复考查紧邻的节点对(p, q)
        if ( p -> data != q -> data ) p = q; //若互异，则转向下一区段
        else remove ( q ); //否则（雷同），删除后者
    return oldSize - _size; //列表规模变化量，即被删除元素总数
}
 
//方法一：//借助函数指针机制遍历
template <typename T>  
void List<T>::traverse ( void ( *visit ) ( T & ) ){   
    for ( ListNodePosi(T) p = header -> succ; p != trailer; p = p -> succ ){ 
        visit ( p -> data );  
    }
}
 
//方法二：//借助函数对象机制遍历
template <typename T> template <typename VST> //元素类型、操作器
void List<T>::traverse ( VST &visit ){  
    for ( ListNodePosi(T) p = header -> succ; p != trailer; p = p -> succ ){
        visit ( p -> data );  
    }
}
 
//遍历输出从r项开始到l项
template <typename T> template <typename VST> //元素类型、操作器
void List<T>::traverse ( VST &visit , ListNodePosi(T) r, ListNodePosi(T) l){  
    for ( ListNodePosi(T) p = r -> pred -> succ; p != l -> succ; p = p -> succ ){
        visit ( p -> data );  
    }
}
 
void show(int e){
    cout << e << " ";
}
 
//列表逆置
template <typename T>
void List<T>::reverse(){
    ListNodePosi(T) p = header;
    for(; p; p = p -> pred){
        std::swap(p -> pred, p -> succ);
    }
    std::swap(header, trailer);     
}
 
//插入排序
template <typename T>  //对起始于位置p的n个元素排序
void List<T>::insertionSort ( ListNodePosi(T) p, int n ){   //valid(p) && rank(p) + n <= size
    for (int r = 0; r <= n; r ++){   //逐一为各节点
        insertA ( search( p -> data, r, p ), p -> data ); //查找适当的位置并插入
        p = p -> succ; remove ( p -> pred ); //转向下一节点
    }
}
 
//selectMax()
template <typename T> //从起始于位置p的n个元素中选出最大者
ListNodePosi(T) List<T>::selectMax (ListNodePosi(T) p, int n){
    ListNodePosi(T) max = p; //最大者暂定为首节点p
    for ( ListNodePosi(T) cur = p; 1 < n; n-- ){ //从首节点p出发，将后续节点逐一与max比较
        if ( !lt ( ( cur = cur->succ )->data, max->data ) ) //若当前元素不小于max，则
            max = cur; //更新最大元素位置记录
    }
    return max; //返回最大节点位置
}
 
//选择排序
template <typename T> //对起始于位置p的n个元素排序
void List<T>::selectionSort ( ListNodePosi(T) p, int n ){   //valid(p) && rank(p) + n <= size
    ListNodePosi(T) head = p -> pred; ListNodePosi(T) tail = p;
    for ( int i = 0; i < n; i ++ ) tail = tail -> succ; //待排序区间为(head, tail)
    while ( 1 < n ){   //在至少还剩两个节点之前，在待排序区间内
        ListNodePosi(T) max = selectMax ( head -> succ, n ); //找出最大者（歧义时后者优先）
        insertB ( tail, remove ( max ) ); //将其移至无序区间末尾（作为有序区间新的首元素）
        tail = tail -> pred; n --;
    }
}
 
//内置归并
template <typename T>
void List<T>::merge(ListNodePosi(T) p, int mid, int n){
    int lenB = mid;
    int lenC = n - mid;
    ListNodePosi(T) A = p;
    T * B = new T[mid];
    for(int i = 0; i<mid; ++i){
        B[i]= p->data; p = p->succ;  
    }
    ListNodePosi(T) C = p;
    for(int j = 0, k = 0; j < lenB; ){
        if( lenC <= k || B[j] <= C->data ){
            A -> data = B[j ++];  
            A = A -> succ;
        }
        if( k < lenC && C -> data < B[j]){
            A -> data = C -> data;  
            A = A -> succ; C = C -> succ; 
            ++ k;
        }  
    }
    delete [] B;
}
 
//归并排序
template <typename T>
void List<T>::mergeSort(ListNodePosi(T) p, int n){
    if( n < 2 ) return ;
    ListNodePosi(T) q = p;
    int mid = n >> 1;
    int x = mid; while(x --) q = q -> succ; 
    mergeSort(p, mid); mergeSort(q, n - mid);
    if(q -> pred -> data > q -> data) merge(p, mid, n);  
}
 
//合并两个链表
template <typename T>
void List<T>::mergeLists(ListNodePosi(T) p, int n, List<T> &L, ListNodePosi(T) q, int  m){
    List<T> t;
    while(m > 0 && n > 0){
        if(p -> data <= q -> data){
            t.insertAsLast(p -> data);
            p = p -> succ;n --;
        }
        else{
            t.insertAsLast(q -> data);
            q = q -> succ;m --;
        }
    }
    while(n > 0) t.insertAsLast(p -> data), p = p -> succ, n --;
    while(m > 0) t.insertAsLast(q -> data), q = q -> succ, m --;
    this -> clear(), L.clear();
    for(ListNodePosi(T) i = t.first(); i != t.trailer; i = i -> succ){
        this -> insertAsLast(i -> data);
    }
    p = this -> first();
}
 
int num[10] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};  //有序数组num
 
void test_01(){
 
    cout << "##### test_01() begin #####" << endl << endl;
 
    cout << "Test List Init :" << endl; 
    List<int> a;
    List<double> b;
    List<List<int>> c;
 
    cout << "RIGHT!" << endl << endl;
 
    cout << "Test List copyNodes():" << endl;
 
    List<int> e;
 
    for(int i = 0; i < 10; i ++) e.insertAsLast(num[i]);
 
    cout << "e = ";
    e.traverse(show, e.first(), e.last());
    cout << endl;
 
    List<int> f(e);
    cout << "f = ";
    f.traverse(show, f.first(), f.last());
    cout << endl;
 
    List<int> g(e.first(), 4);
    cout << "g = ";
    g.traverse(show, g.first(), g.last());
    cout << endl;
 
    cout << "RIGHT!" << endl << endl;
 
    cout << "##### test_01() over #####" << endl;
 
}
 
void test_02(){
 
    cout << "##### test_02() begin #####" << endl << endl;
 
    cout << "Test find() :" << endl;
 
    List<int> a;
 
    for(int i = 0; i < 10; i ++){
        int x = rand() % 20;
        a.insertAsLast(x);
    }    
 
    cout << "a = ";
    a.traverse(show, a.first(), a.last());
    cout << endl;
 
    bool vis_1[101] = {0};
 
    for(int i = 0; i < 10; i ++){
        int x = rand() % 20;
        if(!vis_1[x]) cout << "find(" << x << ") = " << a.find(x) << endl; 
        vis_1[x] = 1;
    }
 
    cout << "RIGHT!" << endl << endl;
 
    cout << "Test search() :" << endl;
 
    List<int> b;
 
    for(int i = 0; i < 10; i ++) b.insertAsLast(num[i]);
 
    cout << "b = ";
    b.traverse(show, b.first(), b.last());
    cout << endl;
 
    int vis_2[101]={0};
 
    for(int i = 0; i < 10; i ++){
        int x = rand() % 20;
        if(!vis_2[x]){
            cout << "search(" << x << ") = " << b.search(x);
            if(b.search(x) == b.last() && b.last() -> data != x) cout << " Not Found!";
            cout << endl;
        }
        vis_2[x] = 1;
    }
 
    cout << "RIGHT!" << endl << endl;
 
    cout << "##### test_02() over #####" << endl;
 
}
 
void test_03(){
 
    cout << "##### test_03() begin #####" << endl << endl;
 
    cout << "Test remove() :" << endl;
 
    List<int> a;
 
    for(int i = 0; i < 10; i ++) a.insertAsLast(num[i]);
 
    cout << "a = ";
    a.traverse(show, a.first(), a.last());
    cout << endl;
 
    cout << "remove(4)" << endl;
    cout << "remove(7)" << endl;
 
    a.remove(a.first() -> succ -> succ -> succ);
    a.remove(a.last() -> pred -> pred -> pred);
 
    cout << "removed a = ";
    a.traverse(show, a.first(), a.last());
    cout << endl;
    cout << "size(a) = " << a.size() << endl;
 
    cout << "RIGHT!" << endl << endl;
 
    cout << "Test clear() : " << endl;
 
    List<int> b(a);
 
    cout << "b = ";
    b.traverse(show, b.first(), b.last());
    cout << endl;
 
    b.clear();
 
    cout << "b.clear(), size(b) = " << b.size() << endl;
 
    cout << "RIGHT!" << endl << endl;
 
    cout << "##### test_03() over #####" << endl;
 
}
 
void test_04(){
 
    cout << "##### test_04() begin #####" << endl << endl;
 
    cout << "Test deduplicate() :" << endl;
 
    List<int> a;
 
    for(int i = 0; i < 20; i ++){
        int x = rand() % 20;
        a.insertAsLast(x);
    }  
 
    cout << "a = ";
    a.traverse(show, a.first(), a.last());
    cout << endl;
 
    a.deduplicate();
 
    cout << "deduplicated a = ";
    a.traverse(show, a.first(), a.last());
    cout << endl;
 
    cout << "RIGHT!" << endl << endl;
 
    cout << "Test uniquify() :" << endl;
 
    List<int> b;
 
    for(int i = 1; i <= 5; i ++){
        for(int j = 0; j < i; j ++){
            b.insertAsLast(i);
        }
    }
 
    cout << "b = ";
    b.traverse(show, b.first(), b.last());
    cout << endl;
 
    b.uniquify();
 
    cout << "uniquifyed b = ";
    b.traverse(show, b.first(), b.last());
    cout << endl;
 
    cout << "RIGHT!" << endl << endl;
 
    cout << "##### test_04() over #####" << endl;
 
}
 
void test_05(){
 
    cout << "##### test_05() begin #####" << endl << endl;
 
    cout << "Test reverse() :" << endl;
 
    List<int> a;
 
    for(int i = 1; i <= 10; i ++) a.insertAsLast(i);
 
    cout << "a = ";
    a.traverse(show, a.first(), a.last());
    cout << endl;
 
    a.reverse();
 
    cout << "reversed a = ";
    a.traverse(show, a.first(), a.last());
    cout << endl;
 
    cout << "RIGHT!" << endl << endl;
 
    cout << "Test sort() :" << endl;
 
    List<int> b;
 
    for(int i = 0; i < 20; i ++){
        int x = rand() % 100;
        b.insertAsLast(x);
    } 
 
    cout << "b = ";
    b.traverse(show, b.first(), b.last());
    cout << endl;
 
    // b.insertionSort(b.first(), b.size());
    // b.insertionSort(b.first(), b.size());
    b.mergeSort(b.first(), b.size());
 
    cout << "sorted b = ";
    b.traverse(show, b.first(), b.last());
    cout << endl;
 
    cout << "RIGHT!" << endl << endl;
 
    cout << "Test mergeLists() :" << endl;
 
    List<int> e,f;
 
    for(int i = 1; i < 20; i += 2) e.insertAsLast(i);
    for(int i = 2; i <= 20; i += 2) f.insertAsLast(i);
 
    cout << "e = ";
    e.traverse(show, e.first(), e.last());
    cout << endl;
 
    cout << "f = ";
    f.traverse(show, f.first(), f.last());
    cout << endl;
 
    e.mergeLists(f);
 
    cout << "e = ";
    e.traverse(show, e.first(), e.last());
    cout << endl;
 
    cout << "RIGHT!" << endl << endl;
 
    cout << "##### test_05() over #####" << endl;
 
}
 
int main(){
 
    cout << "###########################" << endl;
    test_01();
    cout << "###########################" << endl;
    cout << endl;
 
    cout << "###########################" << endl;
    test_02();
    cout << "###########################" << endl;
    cout << endl;
 
    cout << "###########################" << endl;
    test_03();
    cout << "###########################" << endl;
    cout << endl;
 
    cout << "###########################" << endl;
    test_04();
    cout << "###########################" << endl;
    cout << endl;
 
    cout << "###########################" << endl;
    test_05();
    cout << "###########################" << endl;
    cout << endl;
 
    return 0;
 
}

STATISTICS

2.2 列表

2.2.1 从向量到列表

2.2.2 接口

ADT 接口

ListNode 模板类

List 模板类

2.2.3 初始化

头、尾节点

默认构造

由秩到位置的转换

2.2.4 查找

无序列表的顺序查找

有序列表的顺序查找

2.2.5 插入和删除

前插入

后插入

插入接口

删除

时间复杂度

2.2.6 复制构造和析构

copyNodes()

基于复制的构造

列表的清空

列表的析构

2.2.7 去重

无序列表的唯一化

有序列表的唯一化

2.2.8 遍历

2.2.9 逆置和排序

列表逆置

插入排序

选择排序

归并排序

2.2.10 列表测试

发送评论编辑评论

2.2 列表

2.2.1 从向量到列表

2.2.2 接口

ADT 接口

ListNode 模板类

List 模板类

2.2.3 初始化

头、尾节点

默认构造

由秩到位置的转换

2.2.4 查找

无序列表的顺序查找

有序列表的顺序查找

2.2.5 插入和删除

前插入

后插入

插入接口

删除

时间复杂度

2.2.6 复制构造和析构

copyNodes()

基于复制的构造

列表的清空

列表的析构

2.2.7 去重

无序列表的唯一化

有序列表的唯一化

2.2.8 遍历

2.2.9 逆置和排序

列表逆置

插入排序

选择排序

归并排序

2.2.10 列表测试

发送评论 编辑评论

推荐文章

发送评论编辑评论