A. Hello , HAUE
描述
欢迎大家参加河南工程学院2022级第一次新生周赛,LYS代表计算机ACM协会在此祝愿大家的大学生涯一帆风顺,自信满满;友情爱情,两全其美;三阳开泰,学业大展;魅力四射,朋友万千;五福临门,幸福美满;六六大顺,学识博渊;七步之才,知识无边;八仙过海,才华呈现;九霄云外,烦恼抛开;十全十美,大学前途熠熠生辉!!!
输入格式
第一行,输入一个整数 $N$。
输出格式
输出占一行,不含引号。
若 $N = 1$,输出 "One Sail Wind Go"。
若 $N = 6$,输出 "Six Six Big Go"。
若 $N = 10$,输出 "Ten OK Ten OK"。
若 $N = 2022$,输出 "Hello , HAUE"。
样例输入
2022样例输出
Hello , HAUE思想:
- 签到题,考察选择结构。
- 注意 "Hello , HAUE" 的符号是中文,直接复制粘贴。
C代码:
#include <stdio.h>
int main(){
int n;
scanf("%d", &n);
if(n == 1) printf("One Sail Wind Go\n");
else if(n == 6) printf("Six Six Big Go\n");
else if(n == 10) printf("Ten OK Ten OK\n");
else printf("Hello , HAUE\n");
return 0;
}B. 我必须立刻签到,因为它有手就行
描述
在算法竞赛的题目当中,有很多难度逆天的题,然鹅,也有个别的题肥肠煎蛋,像这种HFCJ一看就是"有手就行"的题目就被称之为签到题。
例如这道题目:
f(x)=
\begin{aligned}
\begin{cases}
x^2 &,0\le x\le 10\\\\
x\times f(x - 5) &,10\lt x\le 50\\\\
x + f(x - 10) &,50\lt x\le 100
\end{cases}
\end{aligned}
输入格式
第一行,输入一个整数 $X$。
输出格式
一行,输出按照上述公式计算所得 $X$ 的结果。
数据范围
$0\le X \le 100$
样例输入1
2样例输出1
4样例输入2
11样例输出2
396思想:
- 签到题,考察递归函数。
- 计算后面的数较大,注意开
long long。
C代码:
#include <stdio.h>
#define LL long long
LL f(LL x){
if(x >=0 && x <= 10) return x * x;
else if(x > 10 && x <= 50) return x * f(x - 5);
else return x + f(x - 10);
}
int main(){
LL x;
scanf("%lld",&x);
printf("%lld\n",f(x));
return 0;
}C. OrzOrzOrz
描述
河工院21级计算机学院和软件学院存在着许许多多的大佬,这些大佬都是LYS所膜拜的对象,他们分别是:陈佬(C) ,郭佬(G),皇甫爷(H),金佬(J),李佬(L),魏佬(W),邢佬(X),毅佬(Y),朱佬(Z) 等等诸多大佬(以上排名不分先后,未列出亦视为大佬),由于这些大佬经常水群,所以大家对这些大佬耳熟能详。
每次见到这些大佬在群里出现,LYS就会膜拜一番,发出“OrzOrzOrz”的消息,对于未列出的大佬出现,LYS见到了只敢在心中膜拜,不敢发消息。
一天结束,LYS想要统计今天见到的大佬的次数,可统计实在是个大工程,令LYS肥肠困扰,你能帮助他进行统计吗?
输入格式
第一行输入两个整数 $N$ 和 $M$,代表大佬出现 $N$ 次和 $M$ 次询问。
第二行输入 $N$ 个大写字母 $(A\sim Z)$,代表出现的大佬的编号。
接下来 $M$ 行,每行输入一个大写字母 $(A\sim Z)$,代表询问的大佬编号。
输出格式
对于每次询问:
第一行输出询问编号的大佬出现的次数,若该编号的大佬是上述列出的大佬且出现过,则输出一个空格后输出"OrzOrzOrz"(不加引号)。
数据范围
$0\le N\le 10^4$
$1\le M\le 26$
样例输入
12 6
D N F H L H W Z A W H J
C
Z
W
A
J
H样例输出
0
1 OrzOrzOrz
2 OrzOrzOrz
1
1 OrzOrzOrz
3 OrzOrzOrz思想:
- 只有询问的大佬编号是列出的大佬才会发出 "OrzOrzOrz"。
- 利用
int vis[N]初始化标记,vis[i]表示i是否是列出的大佬。 - 利用
int st[N]记录大佬出现的次数。 - 询问时通过
vis[op[0]]的状态来判断是否是列出的大佬。 - 注意C语言
scanf()读入。
C代码:
#include <stdio.h>
const int N = 1e3 + 10;
int main(){
int st[N]; //记录大佬出现次数
int vis[N]; //标记大佬
for(int i = 'A'; i <= 'Z'; i ++){
if(i == 'C' || i == 'G' || i == 'H' || i == 'J' || i == 'L' || i == 'W' || i == 'X' || i == 'Y' || i == 'Z') vis[i] = 1;
else vis[i] = 0;
st[i] = 0;
}
int n, m;
scanf("%d %d", &n, &m);
for(int i = 1; i <= n; i ++){
char op[10];
scanf("%s", op); //这里读入把空格过滤掉,防止读入奇奇怪怪的东西
st[*op] ++;
}
for(int i = 1; i <= m; i ++){
char op[10];
scanf("%s", op);
if(vis[*op] && st[*op]) printf("%d OrzOrzOrz\n", st[*op]); //*op 等价于 op[0]
else printf("%d\n", st[*op]);
}
return 0;
}C++代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
int st[N];
bool vis[N];
void solve(){
for(int i = 'A'; i <= 'Z'; i ++){
if(i == 'C' || i == 'G' || i == 'H' || i == 'J' || i == 'L' || i == 'W' || i == 'X' || i == 'Y' || i == 'Z') vis[i] = 1;
else vis[i] = 0;
}
int n, m;
cin >> n >> m;
for(int i = 1; i <= n; i ++){
char op;
cin >> op;
st[op] ++;
}
for(int i = 1; i <= m; i ++){
char op;
cin >> op;
if(vis[op] && st[op]) cout << st[op] << " OrzOrzOrz" << endl;
else cout << st[op] << endl;
}
}
int main(){
solve();
return 0;
}D. 红心诡计
描述
Vainglory(虚荣)是由Super Evil Megacorp开发的魔幻风格MOBA类手游,曾依靠超高质量的游戏画质和独特的“点触”操控,在全球收割了千万玩家的喜爱,借助独家的游戏渲染引擎,这款风靡全球的游戏亦曾两度被Apple公司选作Iphone的性能演示宣传片,由该团队首席环境艺术设计师EvilOnTheInside绘制的地图令人着迷。除此之外,独具特色的操控和精心设计的英雄角色,也令Vainglory在MOBA竞技史上给所有人留下了深刻的印象。
可惜的是,由于Vainglory独特的操控模式上手难度极大,以及种种运营不善等原因,导致这款曾经的现象级的游戏在2020年停止了运营,但停服之后,仍有大量热爱Vainglory的玩家活跃在社区服,LYS也不例外。
LYS肥肠喜欢使用剑客黑羽这名角色,因为他不但有爆发性的刺客输出,也有一定的拉扯和扛伤能力,同时还兼具免控与位移为一体的高机动性技能,使得他在单体和团战都能发挥强大的作用。
其中,该英雄的一技能"红心诡计"描述如图:
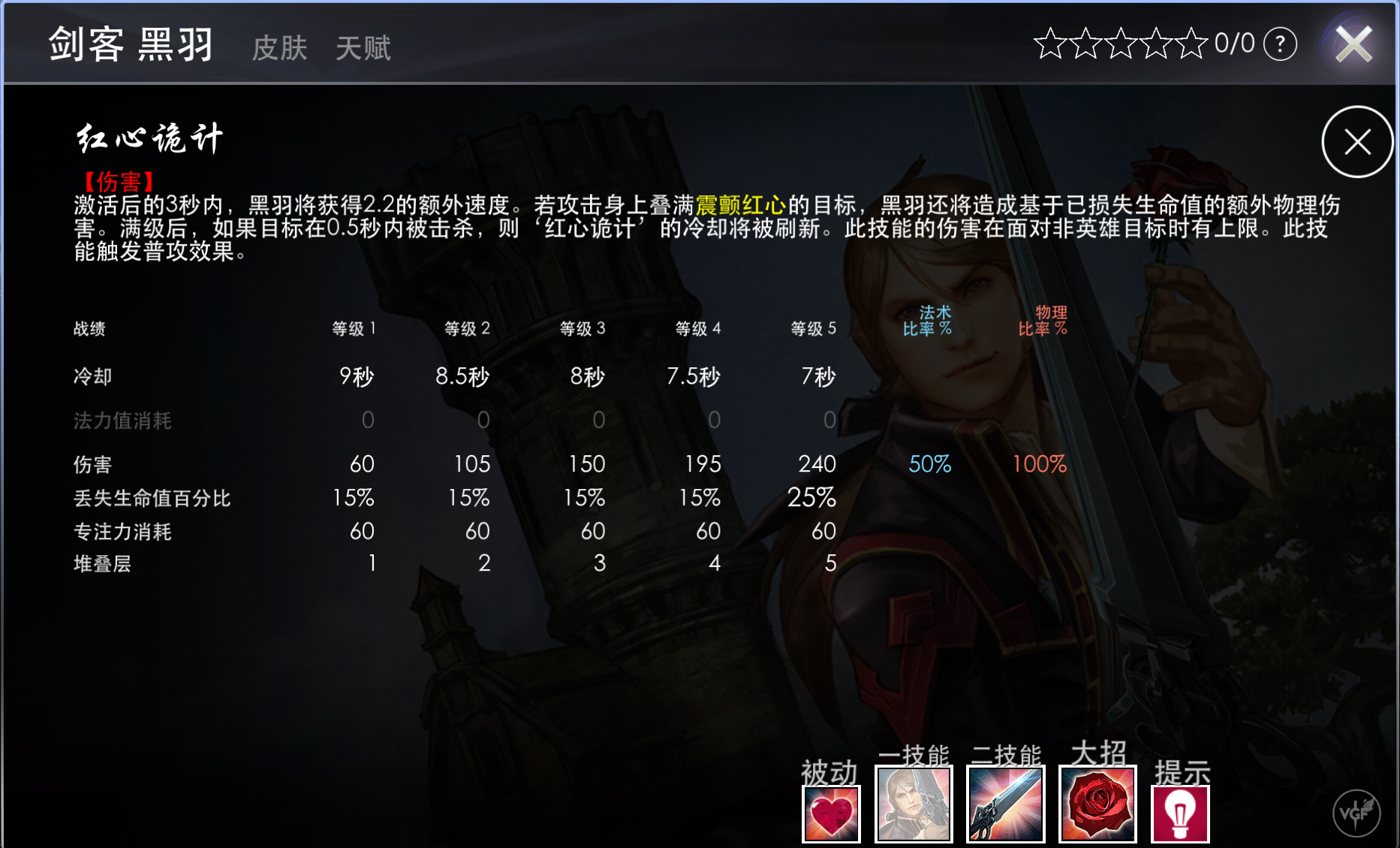
例如:对于某一次正在发生的团战,LYS的黑羽已经将”红心诡计“升至了 $5$ 级,满级的黑羽基础物理普通攻击的伤害是$ 160$,且身上的装备为其提供了 $50$ 点物理强度和 $300$ 点法术强度。
此时LYS遇到了一名敌人,该敌人当前生命值为 $500$,生命值上限为 $2800$,他在敌人到达技能释放范围内时,发动了”红心诡计“,迅速位移至敌人位置对其施加了满层的“震颤红心”并造成伤害,击杀了敌人并刷新了“红心诡计”的冷却时间,其伤害计算如下:
\begin{aligned}
敌人受到的伤害 &= 240(5级技能基础伤害)\\\\
&+ 300 × 50\%(法术强度×法术比率的额外伤害)\\\\
& + 160(该技能触发普通攻击效果,满级黑羽基础物理普通攻击的伤害是160)\\\\
& + 50 × 100\%(物理强度×物理比率的额外伤害)\\\\
&+ 2300 × 25\%(已损失的生命值×5级技能造成的百分比额外伤害)\\\\
&= 1175点!
\end{aligned}
已知:
当前LYS已经将”红心诡计“升至了 $5$ 级,且黑羽的等级已达到最大,其基础物理普通攻击的伤害是 $160$。
求:敌人原地挂机不动,LYS是否可以操作黑羽,在 $(X,Y)$ 处选择任意一个在技能范围 $D$ 之内的敌人开始,使用“红心诡计”位移到其身边击杀敌人并刷新技能,然后选择下一个敌人,如此重复,直到击杀所有的 $5$ 名敌人。若"红心诡计"的范围内不存在敌人或使用一次”红心诡计“无法击杀敌人,LYS将停止后续的操作。
输入格式
第一行 $5$ 个数,分别为黑羽装备的物理强度 $AD$,法术强度 $AP$,黑羽目前的位置横坐标 $X$ 和纵坐标 $Y$,以及以 $(X,Y)$ 为中心的”红心诡计“释放范围半径 $D$。
接下来 $5$ 行,每行四个数,分别为敌人当前所剩的生命值 $L$,生命上限 $R$,以及其位置的横坐标 $x$ 和纵坐标 $y$.
输出格式
第一行,若可以击杀全部敌人,输出”YES“,否则输出”NO“。
若为"NO",第二行额外输出一个整数,表示最大击杀数。
数据范围
$0\le AD,AP,D\le1000$
$-1000\le X,Y,x,y\le 1000$
$1\le L\le R\le5000$
样例输入1
50 200 0 0 3
200 1500 0 3
800 4000 2 2
100 1200 1 1
500 3900 3 0
600 4400 4 3样例输出1
YES样例输入2
100 30 -1 1 4.2
1500 1900 1.2 0.8
140.9 892.6 3.1 2.2
230 556.9 4.4 -1
530 2799.2 -2.5 -2
462.6 3784 2.9 -1.1样例输出
NO
1提示
对于样例 $1$,可行的情况为从 $(0,0)$ 开始,先击杀 $(0,3)$ 刷新了技能,然后击杀 $(1,1)$ 再次刷新技能,接着击杀 $(3,0)$,$(2,2)$,$(4,3)$ 或者从 $(0,0)$ 开始,先击杀 $(3,0)$ 刷新了技能,然后击杀 $(1,1)$ 再次刷新技能,接着击杀 $(0,3)$,$(2,2)$,$(4,3)$。
思想1:
- 由题意可知,要求从$(X,Y)$开始,在$D$范围内,可以任意选择一个$(x,y)$位置的敌人,如果可以将其击杀,则可以将$(X,Y)$更新为$(x,y)$,继续寻找在其$D$范围内的敌人击杀,直至$D$范围内没有敌人,或下一次无法击杀敌人。
- 对于本题,敌人数量只有$5$,可以暴力枚举:
- 第一层循环枚举敌人
i,判断(X,Y)是否与(x[i],y[i])距离小于d,且若可以将其击杀,则进入下一层循环。 - 在下一层循环开始前,我们利用
int vis[N],vis[i]来标记i号敌人已经被击杀,以后不再枚举i,用cnt记录击杀数。 - 第二层循环枚举敌人
j,判断(x[i],y[i])是否与(x[j],y[j])距离小于d,且若可以将其击杀,则进入下一层循环。 - 在下一层循环开始前,标记
vis[j],且cnt ++。 - 第三层循环枚举敌人
q,判断(x[j],y[j])是否与(x[q],y[q])距离小于d,且若可以将其击杀,则进入下一层循环。 - 在下一层循环开始前,标记
vis[q],且cnt ++。 - $\dots$
- 直到枚举到最后一个敌人,在每一层循环退出之后更新
res,还要将敌人和击杀数恢复为上一层的进入状态。
- 第一层循环枚举敌人
C语言代码:
#include <stdio.h>
//check函数判断是否满足继续的条件
int check(double x1, double y1, double x2, double y2, double d, double l, double r, double ap,double ad){
if((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2) <= d * d){
if(l <= (r - l) * 0.25 + ap * 0.5 + 240 + 160 + ad) return 1;
else return -1;
}
else return -1;
}
int main(){
int check(double x1, double y1, double x2, double y2, double d, double l, double r, double ap,double ad);
double ap, ad, X, Y, d;
scanf("%lf %lf %lf %lf %lf", &ad, &ap, &X, &Y, &d);
double l[10], r[10], x[10], y[10];
for(int i = 1; i <= 5; i ++) scanf("%lf %lf %lf %lf", &l[i], &r[i], &x[i], &y[i]);
int res = 0; //res存储可以击杀的最大敌人数量
for(int i = 1; i <= 5; i ++){ //第一层循环,判断从(X,Y)开始能否击杀 i 号敌人
int cnt = 0; //表示当前击杀数
if(check(X, Y, x[i], y[i], d, l[i], r[i], ap, ad) < 0) continue; //不能击杀则跳过
//能击杀 i
int vis[10]; //vis[*]存储第 * 号敌人是否已经击杀
for(int k = 1; k <= 5; k ++) vis[k] = 0; //初始化全部敌人未击杀
vis[i] = 1; //标记 i 已经被击杀
cnt ++; //击杀数加一
for(int j = 1; j <= 5; j ++){ //第二层循环,判断击杀 i 后,剩下的敌人 j 是否可以击杀
if(vis[j] || check(x[i], y[i], x[j], y[j], d, l[j], r[j], ap, ad) < 0) continue;
//能击杀 j
vis[j] = 1; //标记 j 已经被击杀
cnt ++;
for(int q = 1; q <= 5; q ++){ //第三层循环,判断击杀 j 后,剩下的敌人 q 是否可以击杀
if(vis[q] || check(x[j], y[j], x[q], y[q], d, l[q], r[q], ap, ad) < 0) continue;
vis[q] = 1;
cnt ++;
for(int w = 1; w <= 5; w ++){
if(vis[w] || check(x[q], y[q], x[w], y[w], d, l[w], r[w], ap, ad) < 0) continue;
vis[w] = 1;
cnt ++;
for(int e = 1; e <= 5; e ++){ //最后一个循环,判断第五个敌人是否可以击杀
if(vis[e] || check(x[w], y[w], x[e], y[e], d, l[e], r[e], ap, ad) < 0) continue;
vis[e] = 1;
cnt ++;
break;
}
//结束每一层的循环后
res = res > cnt ? res : cnt; //更新最大击杀数
vis[w] = 0; //恢复原有的敌人状态(变为未击杀)
cnt --; //恢复击杀数
}
res = res > cnt ? res : cnt;
vis[q] = 0;
cnt --;
}
res = res > cnt ? res : cnt;
vis[j] = 0;
cnt --;
}
res = res > cnt ? res : cnt; //最后的更新
}
if(res == 5) printf("YES\n");
else printf("NO\n%d\n",res);
return 0;
}思想2:
DFS搜索。- 利用递归的每一层代替暴力循环嵌套。
另一种暴力搜索的思路:
- 对所有的敌人击杀顺序的组合进行全排列,依次判断每一种排列组合的最大击杀数。
C++代码:
#include <bits/stdc++.h>
using namespace std;
bool check(double x1, double y1, double x2, double y2, double d, double l, double r, double ap,double ad){
if((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2) <= d * d){
if(l <= (r - l) * 0.25 + ap * 0.5 + 240 + 160 + ad) return true;
else return false;
}
else return false;
}
struct point{
double l, r, x, y;
}p[10];
int res;
bool vis[10];
void dfs(double xx, double yy, double d, double ap,double ad, int u){
for(int i = 1; i <= 5; i ++){
if(!vis[i] && check(xx, yy, p[i].x, p[i].y, d, p[i].l, p[i].r, ap, ad)){
vis[i] = 1;
dfs(p[i].x, p[i].y, d, ap, ad, u + 1);
vis[i] = 0; //恢复状态
}
}
res = max(res, u); //更新击杀数
return ;
}
int main(){
double ad, ap, X, Y, d;
cin >> ad >> ap >> X >> Y >> d;
for(int i = 1; i <= 5; i ++){
double l, r, x, y;
cin >> l >> r >> x >> y;
p[i] = {l, r, x, y};
}
for(int i = 1; i <= 5; i ++){
memset(vis, 0, sizeof vis); //初始化标记
dfs(X, Y, d, ap, ad, 0);
}
if(res == 5) cout << "YES" << endl;
else cout << "NO" << endl << res << endl;
return 0;
}E. 不要停下来啊!!!
描述
新的学期开始了,我们的奥尔加团长又一次嘱托我们,无论以后学习遇到什么困难,都请记住:“不要停下来啊!!!”

输入格式
同样例输入
第一行输入三个整数 $N,M,K$,代表一个 $N$ 行 $M$ 列的二维数组和 $K$ 行坐标信息
接下来共 $K$ 行,每行输入两个整数 $x,y$,对于二维数组 $(x,y)$ 位置的点标记为"#",未被标记的点记为"."
输出格式
同样例输出(注意每个字符间隔一个空格)
样例输入
15 9 44
0 2
1 1
2 1
3 1
3 3
3 4
4 1
4 3
4 4
5 1
5 2
5 3
5 4
5 5
5 6
6 2
6 3
6 4
6 5
6 6
7 2
7 3
7 4
7 5
7 6
8 2
8 3
8 4
8 5
8 6
9 3
9 4
9 6
10 3
10 5
10 7
11 3
11 6
12 3
12 6
13 3
13 6
14 3
14 6样例输出
. . # . . . . . .
. # . . . . . . .
. # . . . . . . .
. # . # # . . . .
. # . # # . . . .
. # # # # # # . .
. . # # # # # . .
. . # # # # # . .
. . # # # # # . .
. . . # # . # . .
. . . # . # . # .
. . . # . . # . .
. . . # . . # . .
. . . # . . # . .
. . . # . . # . .注意:
- 该二维数组下标从 $(0,0)$ 开始。
思想1:
- 签到题,考察二维数组。
C代码1:
#include <stdio.h>
int main(){
char mp[100][100];
int n, m, k;
scanf("%d %d %d", &n, &m, &k);
for(int i = 0; i < n; i ++){
for(int j = 0; j < m; j ++){
mp[i][j] = '.';
}
}
for(int i = 1; i <= k; i ++){
int x, y;
scanf("%d %d", &x, &y);
mp[x][y] = '#';
}
for(int i = 0; i < n; i ++){
for(int j = 0; j < m; j ++){
printf("%c ",mp[i][j]);
}
printf("\n");
}
return 0;
}思想2:
- 样例输出即为答案,直接打表也可以。
C代码2:
#include <stdio.h>
int main(){
printf(". . # . . . . . .\n");
printf(". # . . . . . . .\n");
printf(". # . . . . . . .\n");
printf(". # . # # . . . .\n");
printf(". # . # # . . . .\n");
printf(". # # # # # # . .\n");
printf(". . # # # # # . .\n");
printf(". . # # # # # . .\n");
printf(". . # # # # # . .\n");
printf(". . . # # . # . .\n");
printf(". . . # . # . # .\n");
printf(". . . # . . # . .\n");
printf(". . . # . . # . .\n");
printf(". . . # . . # . .\n");
printf(". . . # . . # . .\n");
return 0;
}F. 反卷行动
描述
众所周知,河工院的计算机学院和软件学院存在着许多大佬,这些大佬们每天最喜欢做的事情就是口口声声的称:"今天又是摆烂的一天,啥也没干",其实背地里却是名副其实的"卷王",私底下学了不少东西
LYS心中大惊Σ(っ °Д °;)っ!他说:“这样好吗?这不好!”
LYS深知卷王的可怕,靠近卷王的人迟早也会被卷王传染,进而也会变成卷王,如此下去,所有人都将被卷,这太可怕了!
可惜的是,变成卷王的人再也变不会原来的样子了,所以LYS只能尽可能的想办法守护还没有变成卷王的人。
为了顺利开展反卷行动,LYS以每一个寝室为单位进行守护,他发现寝室的排列整好是按照 $1\sim N$ 的编号围成了一圈,并且他将有卷王存在的 $M$ 个宿舍都打上了标记。
已知有卷王存在的宿舍 $Mi$ 经过一个夜晚的奋战,会将其相邻的两个宿舍($M{i-1}$和$M_{i+1}$)的人全部变成卷王(编号为 $M_N$ 的宿舍相邻宿舍是 $M1$ 和 $M{N-1}$),LYS可以在夜晚降临之前据守在任意一个没有卷王存在的宿舍 $M_j$,使其宿舍内的所有人获得“反卷之力”,获得“反卷之力”的宿舍在今晚不会被变成卷王,且以后也不会被变成卷王。
由于LYS太弱小了,他一天只能保护一个宿舍,但是LYS想要保护尽可能多的宿舍,因此他需要精心策划每一次的据点,由于LYS孤军奋战,他需要一个人帮他谋划据点宿舍的选择,你能帮帮他吗?
输入格式
第一行输入两个整数 $N,M$,分别代表寝室最大编号和卷王宿舍的数量。
第二行 $M$ 个数,表示卷王宿舍的编号 $m_i$。
输出格式
输出一个整数,输出最终没有被变成卷王的宿舍数量。
数据范围
$5\le N \le 10^9$
$1\le M\le min(N,2\times 10^5)$
$1\le m_i\le N$
样例输入1
6 2
3 5样例输出1
2样例输入2
12 2
8 2样例输入2
5思想:
- 贪心。
- 每次选择未被变成卷王(未被感染)宿舍的最长区间进行保护。
- 对于被保护的区间
[l,r]:- 经过第一天:
- 保护
[l,r]的一个端点,设保护a[l]。 a[l]不会感染,a[r]会被感染。- 其他所有未受到保护的区间
[l',r']里,a[l']和a[r']被感染。 - 经过第二天:
- 保护
[l,r]的另一个端点a[r],由于第一天a[r]被感染,故只能保护a[r - 1]。 - 其他所有未受到保护的区间
[l',r']里,a[l' + 1]和a[r' - 1]被感染。 - 即对于选择保护的区间
[l,r],a[r]被感染,我们只能保护到[l,r - 1]这一段,且其余所有未受到保护的区间[l',r']里a[l'],a[r'],a[l' + 1],a[r' - 1]受到感染,感染后的区间变为[l' + 2, r' - 2]。
- 综上可知,我们优先保护最长的未被变成卷王的区间,即可实现最优策略。
- 由于选择保护的区间端点可以任选,故只需要考虑区间长度,不需要维护额外的信息。
- 注意不要忽略首尾相连的区间。
注意:
- 本题的数据卡掉了冒泡排序的可能性,选手可选择任意一种时间复杂度优于冒泡排序的方法进行处理。
- 以
C++的sort()排序函数为例,给出如下代码1,以优先队列维护最长区间为例,给出如下代码2。 sort()用法参考:std::sort。
C++代码1:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e7 + 10;
int a[N], b[N];
int main(){
int n, m;
scanf("%d %d", &n, &m);
for(int i = 0; i < m; i ++) scanf("%d", &a[i]); //读入所有卷王的房间编号
sort(a, a + m); //将卷王房间的编号从小到大排序
int idx = 0; //idx作为被保护的区间数组b的下标
b[idx ++] = n - a[m - 1] + a[0] - 1; //将首尾相连的区间加入
for(int i = 0; i < m - 1; i ++) b[idx ++] = a[i + 1] - a[i] - 1;
sort(b, b + idx, greater<int>()); //将区间长度从大到小排序
int res = 0;
for(int i = 0; i < idx; i ++){
int k = 0;
if(b[i] - i * 4 > 0){ //完全保护好当前区间需要两天,则未被保护的区间由于两端均会被感染,故两天会损失4个宿舍
k = b[i] - i * 4; //经过i天后未被保护的区间在受到保护时剩下的还未变成卷王的区间长度
if(k > 1) k --; //两天里一天只能保护一端,另一端会被感染
res += k;
}
else break;
}
printf("%d\n",res);
return 0;
}C++代码2:
#include <bits/stdc++.h>
using namespace std;
void solve(){
int n, m;
cin >> n >> m;
vector<int> vis; //vis存储最先被感染的房屋编号
for(int i = 0; i < m; i ++){
int x;
cin >> x;
vis.push_back(x);
}
sort(vis.begin(),vis.end()); //将编号从小到大排序
priority_queue<int> st; //优先队列维护当前最大长度的区间
st.push(n - vis.back() + vis[0] - 1); //将首尾相连的区间长度加入
for(int i = 0; i + 1 < vis.size(); i ++){
st.push(vis[i + 1] - vis[i] - 1); //将未感染的区间的长度加入
}
int cnt = 0; //存储未感染的区间长度
for(int i = 0; i + 1 > 0; i ++){ //i代表天数
if(!st.empty() && st.top() - i * 4 > 0){ //经过一天,下一个区间长度 -4
int k = st.top() - i * 4; //设k为当前区间经过i天后未感染的区间长度
if(k > 1) k --; //对于一个端点的保护,会使另一个端点被感染(长度-1),若区间长度仅为1,则只能保护1长度
cnt += k; //累计保护到的区间长度
st.pop();
}
else break;
}
cout << cnt << endl;
}
int main(){
solve();
return 0;
}G. 机器人OR寄器人
描述
随着新学期的开始,HFCJ学长准备开发一个可以接收指令从而行动的机器人,现在硬件部分的设计已经解决,只剩下编辑指令和处理的部分。可是这种小事对他来说太简单了,用他的原话说就是:"有手就行",于是他就懒得继续做下去了。
HFCJ把这个做了一半的机器人丢给了LYS,如果他能完成剩余的工作,并且成品能够通过测试,那么这个机器人就归LYS辣。
以下是待完成的任务要求:
- 要求能够存储多个指令,在测试时执行对应编号的指令
- 添加指令:输入一个整数 $P$,表示添加的指令编号,然后输入两个整数 $x,y$,作为执行信息存储。
- 执行指令:输入一个整数 $Q$,表示执行的指令编号,然后执行该指令的信息 $x_q,y_q$,使得机器人从原位置 $(X,Y)$ 移动到 $(X+x_q,Y+y_q)$。
LYS肥肠想要这个机器人,可是他啥也不会,现在他来找你帮忙了,你能帮帮他吗?
输入格式
第一行输入四个整数 $N,M,X,Y$,分别表示添加 $N$ 个指令和 $M$ 次执行,以及机器人的起始坐标 $(X,Y)$。
接下来 $N$ 行,第 $i(1\sim N)$ 行输入两个整数 $x_i,y_i$,表示 $i$ 号指令的执行信息。
然后一行,输入 $M$ 个整数,$M_i$ 为执行的指令编号。
输出格式
一行,输出两个整数,表示执行完所有指令后机器人的坐标。
数据范围
$1\le N,M\le 1000$
$-1000\le X,Y,x,y\le 1000$
样例输入
3 4 0 0
1 1
-1 -1
2 2
1 3 2 2样例输出
1 1思想:
- 构造偏移量数组
dx[N],dy[N],存储编号的信息。 - 执行指令编号为
q,则使X和Y加上对应编号的偏移量,即X += dx[q], Y += dy[q]。
C代码
#include <stdio.h>
int main(){
int dx[1010], dy[1010];
int n, m, X, Y;
scanf("%d %d %d %d", &n, &m, &X, &Y);
for(int i = 1; i <= n; i ++) scanf("%d %d", &dx[i], &dy[i]);
for(int i = 1; i <= m; i ++){
int q;
scanf("%d", &q);
X += dx[q];
Y += dy[q];
}
printf("%d %d\n", X, Y);
return 0;
}H. 帕秋莉GO!!!
描述
众嗦♂粥汁,帕秋莉·诺蕾姬是《东方Project》系列弹幕游戏及其衍生作品的登场角色之一。
她是大小姐蕾米莉亚的好朋友,是个大概有100岁的魔女。她居住在幻想乡中藏书最多的大图书馆——红魔馆地下图书馆中。喜欢读书,并且会使用七曜魔法。
贤者(Philosopher)的另一个意思是哲学家,因此也可称她为七曜的哲♂学家。平常总待在大图书馆里的她,患有哮喘、贫血,体质虚弱,因此在肉搏♂战中非常劣势。
在比利王客串的兄贵本篇TalesFromTheFoxhole里,作为军官的比利对于下属的小兵在休息时间感到不满而发出的“Attention on”因为音质问题常被空耳成“帕秋莉♂GO”。

由于某种不可知的异变,姆Q穿越到了知名演员野兽♂仙贝的家中,这名不谙世事的马猴烧酒头一次从红魔馆的地下走出,没想到居然会收获颇丰,她在野兽♂仙贝的激情指导下学习到了她从未见识过的膜法,只不过由于哮喘的原因,导致她无法将这强大的咒语一次性咏唱完毕。
我们的姆Q非常困扰,她决定将这条强大的咒语告诉你,想借助科学的力量完成咏唱,你能帮帮她吗?
咒语:持续进行咏唱“114514”直到达到“1919“次。
输入格式
无。
输出格式
每行输出"114514"(不包含引号),共输出1919行。
思想:
- 签到题,考察循环结构。
C代码:
#include <stdio.h>
int main(){
for(int i = 1; i <= 1919; i ++) printf("114514\n");
return 0;
}
膜拜大佬