A 4497. 分糖果
描述
给定三个正整数 $a,b,c$。
请计算 $⌊\frac{a+b+c}{2}⌋$,即 $a,b,c $相加的和除以$ 2 $再下取整的结果。
输入格式
第一行包含整数 $T$,表示共有 $T $组测试数据。
每组数据占一行,包含三个正整数 $a,b,c$。
输出格式
每组数据输出一行结果,表示答案。
数据范围
前三个测试点满足$ 1≤T≤10$。
所有测试点满足$ 1≤T≤1000,1≤a,b,c≤10^{16}$。
输入样例:
4
1 3 4
1 10 100
10000000000000000 10000000000000000 10000000000000000
23 34 45输出样例:
4
55
15000000000000000
51思想
- 数据范围极大,高精度计算
- 板子题,没什么好说的
模板
- 倒序
vector<int>存储A和B,进行高精度A和B加法运算 - 倒序
vector<int>存储A,进行高精度除低精度b运算
//高精度加法
vector<int> add(vector<int> &A,vector<int> &B){
if(A.size()<B.size()) return add(B,A); //判断A和B的长度
int k=0; //定义进位,初始化为0
vector<int> C; //存储答案
for(int i=0;i<A.size();i++){ //遍历模拟
k+=A[i]; //进位加A本位
if(i<B.size()) k+=B[i]; //如果B未遍历完,则加上B本位
C.push_back(k%10); //存入答案
k/=10; //更新进位
}
if(k) C.push_back(k); //如果最后进位非零,则补上进位
return C;
}
//高精度除法
vector<int> div(vector<int> &A,int b,int &r){
vector<int> C; //存储答案
r=0; //初始化余数为0
for(int i=A.size()-1;i>=0;i--){ //从最高位开始遍历
int k=r*10+A[i]; //定义除数k为余数r*10加A本位
C.push_back(k/b); //存入答案
r=k%b; //更新余数
}
reverse(C.begin(),C.end()); //由于答案从最高位开始存入,故需翻转
while(C.size()>1&&C.back()==0) C.pop_back(); //去除前导0
return C;
}代码
#include<bits/stdc++.h>
using namespace std;
vector<int> add(vector<int> &A, vector<int> &B)
{
if (A.size() < B.size()) return add(B, A);
vector<int> C;
int t = 0;
for (int i = 0; i < A.size(); i ++ )
{
t += A[i];
if (i < B.size()) t += B[i];
C.push_back(t % 10);
t /= 10;
}
if (t) C.push_back(t);
return C;
}
vector<int> div(vector<int> &A, int b, int &r)
{
vector<int> C;
r = 0;
for (int i = A.size() - 1; i >= 0; i -- )
{
r = r * 10 + A[i];
C.push_back(r / b);
r %= b;
}
reverse(C.begin(), C.end());
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
void solve(){
vector<int> A,B,C;
string a, b, c;
int r;
cin >> a >> b >> c;
for(int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0'); //倒序存储
for(int i = b.size() - 1; i >= 0; i--) B.push_back(b[i] - '0');
for(int i = c.size() - 1; i >= 0; i--) C.push_back(c[i] - '0');
vector<int> D = add(A,B);
vector<int> E = add(C,D); //E = A + B + C
vector<int> F = div(E,2,r);
for(int i = F.size() - 1; i >= 0; i--) cout << F[i];
cout << endl;
}
int main(){
int _;
cin >> _;
while(_--){
solve();
}
return 0;
}
B 4498. 指针
描述
给定一个如下图所示的全圆量角器。
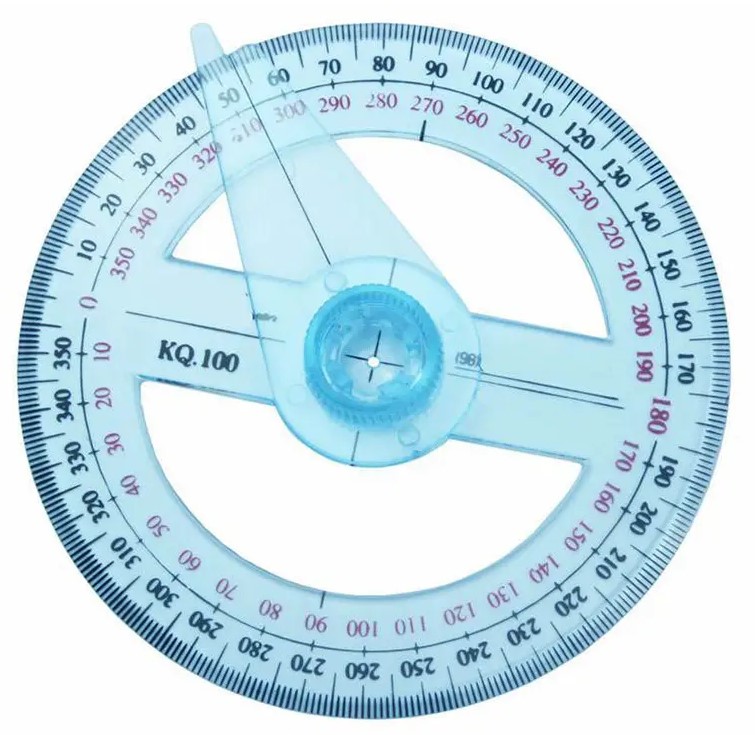
初始时,量角器上的指针指向刻度 0。
现在,请你对指针进行 n 次拨动操作,每次操作给定一个拨动角度 ai,由你将指针拨动 ai 度,每次的拨动方向(顺时针或逆时针)由你自由决定。
请你判断,能否通过合理选择每次拨动的方向,使得指针最终仍然指向刻度 0。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一个整数 ai,表示一次操作的拨动角度。
输出格式
如果可以做到指针最终仍然指向刻度 0,则输出 YES,否则输出 NO。
数据范围
前 4 个测试点满足 1≤n≤3。
所有测试点满足 1≤n≤15,1≤ai≤180。
输入样例1:
3
10
20
30输出样例1:
YES输入样例2:
3
10
10
10输出样例2:
NO输入样例3:
3
120
120
120输出样例3:
YES思想
- 设当所有操作结束后,转过的角度大小为$P$
- 当且仅当$360|P$时,可以回到原点
- 考虑
dfs,递归第$i$层表示为第$i$次操作
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 3;
int a[N];
int n;
bool flag;
void dfs(int u,int p)
{
if(u > n){
if(p % 360 == 0){
flag = 1;
}
return ;
}
dfs(u + 1,p + a[u]); //顺时针旋转
dfs(u + 1,p - a[u]); //逆时针旋转
}
int main(){
cin >> n;
for(int i = 0; i < n; i++) cin >> a[i];
dfs(0,0);
if(flag) cout << "YES" << endl;
else cout << "NO" << endl;
return 0;
}C 4499. 画圆
描述
在一个二维平面内,给定一个以 (x1,y1) 为圆心,半径为 R 的圆以及一个坐标为 (x2,y2) 的点。
请你在二维平面上画一个圆,要求:
平面中不存在点满足既在你画的圆上,又在给定的圆外。
给定的点不能在你画的圆内(可以在圆上)。
被给定圆覆盖且不被你画的圆覆盖的区域面积应尽可能小。
请输出你画的圆的圆心坐标以及半径。
输入格式
共一行,包含 5 个整数 R,x1,y1,x2,y2。
输出格式
三个实数 xans,yans,r,其中 (xans,yans) 是你画的圆的圆心坐标,r 是你画的圆的半径。
结果保留六位小数。
数据范围
所有测试点满足 1≤R≤105,|x1|,|y1|,|x2|,|y2|≤105。
输入样例1:
5 3 3 1 1输出样例1:
3.767767 3.767767 3.914214输入样例2:
10 5 5 5 15输出样例2:
5.000000 5.000000 10.000000思想
- 分析题目可知:
- 圆要画在给定圆内
- 当给定点在给定圆外或圆上时,答案就是给定的圆
- 当给定点在圆内时,要使要求3中面积最小,则画的圆尽量大,所以半径尽量大
代码
#include <bits/stdc++.h>
using namespace std;
void solve(){
double r, x_1, y_1, x_2, y_2;
scanf("%lf%lf%lf%lf%lf", &r, &x_1, &y_1, &x_2, &y_2);
double l = (x_1 - x_2) * (x_1 - x_2) + (y_1 - y_2) * (y_1 - y_2);
if (l == 0){ //重合
printf("%.6lf %.6lf %.6lf", x_1 + (r / 2), y_1, r / 2);
}
else if (l < r * r && l){
l = sqrt(l);
double d = l + r; //给定点与圆心的距离加上给定圆的半径即为该情况下半径的最大值
double r_1 = d / 2.0; //半径
double l_1 = y_1 - y_2;
double l_2 = x_1 - x_2;
double x_3 = (x_1 + x_2 + (r * l_2 / l)) / 2;
double y_3 = (y_1 + y_2 + (r * l_1 / l)) / 2;
printf("%.6lf %.6lf %.6lf", x_3, y_3, r_1);
}
else{
printf("%.6lf %.6lf %.6lf", x_1, y_1, r);
}
}
int main(){
solve();
return 0;
}