本文最后更新于 1354 天前,其中的信息可能已经有所发展或是发生改变。
例题 843. n-皇后问题
描述
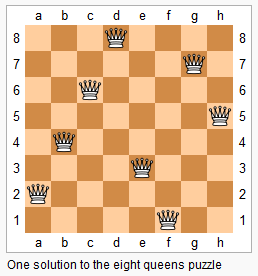
n−皇后问题是指将 n 个皇后放在 n×n 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。
现在给定整数 n,请你输出所有的满足条件的棋子摆法。
输入格式
共一行,包含整数 n。
输出格式
每个解决方案占 n 行,每行输出一个长度为 n 的字符串,用来表示完整的棋盘状态。
其中 . 表示某一个位置的方格状态为空,Q 表示某一个位置的方格上摆着皇后。
每个方案输出完成后,输出一个空行。
注意:输出顺序要按照样例的规律
数据范围
1≤n≤9
输入样例:
4输出样例:
.Q..
...Q
Q...
..Q.
..Q.
Q...
...Q
.Q..分析
- 由于皇后不能互相攻击到,故棋盘的每一行,每一列及其有皇后存在的对角线的平行线上有且只有一个皇后
- 递归处理,每一次递视为一次对棋子的判断,递归的层数视为棋盘的层数,每一层选择放置一个皇后
- 对于递归的每一层,遍历这层棋盘的格子,判断以该格子的列和对角线的平行线上是否存在过皇后
- 若放置皇后,则需要对放置的格子所在的列和对角线的平行线进行标记,并将其记录在答案数组中
- 递归处理上述过程,直到将皇后放置完毕,此时遍历答案数组输出一次排列
- 对于对角线的处理,我们 可以利用数学关系,转换为截距进行标记
k = i + u或k = i - u
代码
#include <bits/stdc++.h>
using namespace std;
const int N=100;
int n;
char mp[N][N]; //当前棋盘的状态
bool y[N],l[N],r[N]; //标记是否存在过皇后
void dfs(int u){
if(u==n+1){ //当u=n+1时说明第n层的棋盘已经放置完毕,输出一次可能性
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
cout<<mp[i][j];
}
cout<<endl;
}
cout<<endl;
return ;
}
for(int i=1;i<=n;i++){
if(!y[i]&&!l[u-i+n]&&!r[u+i+n]){ //若该点所在的列及其所在的对角线的平行线不曾出现过皇后
y[i]=l[u-i+n]=r[u+i+n]=1; //标记
mp[u][i]='Q'; //放置皇后
dfs(u+1); //递归到下一层
mp[u][i]='.'; //回溯
y[i]=l[u-i+n]=r[u+i+n]=0;
}
}
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){ //初始化
for(int j=1;j<=n;j++){
mp[i][j]='.';
}
}
dfs(1);
return 0;
}