3.1 简单搜索
分类
- DFS
- BFS
- A* (BFS+贪心)
- 双向广搜
- 双端队列广搜
- 双向DFS
- IDDFS (DFS+BFS)
- IDA* (IDDFS优化)
3.1.1 BFS
思想
- 当题目需要对一组数据进行扩展式搜索时可以考虑
BFS - 搜索时要将已经满足要求的点入队
- 不断地弹出队头,以队头元素进行扩展搜索,可以得到若干新的元素
- 对这些元素进行判断,满足继续搜索的条件则将该元素入队,否则具体问题具体分析,标记或抛弃。
- 一般来说,
BFS在第一次搜到答案时可以直接返回值,提前结束搜索
例题 844. 走迷宫
描述
给定一个 n×m 的二维整数数组,用来表示一个迷宫,数组中只包含 0 或 1,其中 0 表示可以走的路,1 表示不可通过的墙壁。
最初,有一个人位于左上角 (1,1) 处,已知该人每次可以向上、下、左、右任意一个方向移动一个位置。
请问,该人从左上角移动至右下角 (n,m) 处,至少需要移动多少次。
数据保证 (1,1) 处和 (n,m) 处的数字为 0,且一定至少存在一条通路。
输入格式
第一行包含两个整数 n 和 m。
接下来 n 行,每行包含 m 个整数(0 或 1),表示完整的二维数组迷宫。
输出格式
输出一个整数,表示从左上角移动至右下角的最少移动次数。
数据范围
1≤n,m≤100
输入样例:
5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0输出样例:
8代码
#include <bits/stdc++.h>
using namespace std;
const int N=110;
int mp[N][N]; //记录地图
bool vis[N][N]; //标记该点是否走过
int ans[N][N]; //存储答案
int n,m;
struct point{ //初始化point为struct类型
int x,y;
};
int dx[]={0,0,1,-1},dy[]={1,-1,0,1};
int bfs(){
queue<point> st; //定义队列
st.push({1,1}); //将起始点的信息入队
vis[1][1]=1; //标记起始点已经走过
while(!st.empty()){
auto p=st.front(); //使p获得队头的信息
st.pop(); //将队头出队
for(int i=0;i<4;i++){ //循环遍历偏移量数组,搜索四个方向
int l=p.x+dx[i],r=p.y+dy[i];
if(l>=1&&l<=n&&r>=1&&r<=m&&mp[l][r]==0&&!vis[l][r]){ //判断该点是否满足搜索条件
ans[l][r]=ans[p.x][p.y]+1; //更新答案
if(l==n&&r==m) return ans[n][m]; //搜到答案直接返回
vis[l][r]=1; //标记该点已经走过
st.push({l,r}); //将该点入队,后续继续扩展该点搜索
}
}
}
return ans[n][m]; //没有提前搜到答案,最后返回答案
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>mp[i][j];
}
}
cout<<bfs()<<endl;
return 0;
}例题 走出迷宫
描述
小明现在在玩一个游戏,游戏来到了教学关卡,迷宫是一个N*M的矩阵。
小明的起点在地图中用“S”来表示,终点用“E”来表示,障碍物用“#”来表示,空地用“.”来表示。
障碍物不能通过。小明如果现在在点(x,y)处,那么下一步只能走到相邻的四个格子中的某一个:(x+1,y),(x-1,y),(x,y+1),(x,y-1);
小明想要知道,现在他能否从起点走到终点。
输入格式:
本题包含多组数据。
每组数据先输入两个数字N,M
接下来N行,每行M个字符,表示地图的状态。
数据范围:
2<=N,M<=500
保证有一个起点S,同时保证有一个终点E.
输出格式:
每组数据输出一行,如果小明能够从起点走到终点,那么输出Yes,否则输出No
输入样例:
3 3
S..
..E
...
3 3
S##
###
##E输出样例
Yes
No分析
- 走出迷宫需要对每一个点进行搜索
- 首先需要记录
S的坐标 - 从
S开始搜索,需要偏移量数组 - 对于
BFS在搜随时,若搜到E点直接返回
BFS代码
#include <bits/stdc++.h>
using namespace std;
const int N=510;
int n,m;
char mp[N][N]; //存储地图
bool vis[N][N]; //标记是否走过该点
int s1,s2; //标记S的坐标
int dx[]={0,0,1,-1},dy[]={1,-1,0,0}; //初始化偏移量数组
struct point{ //用于记录点的信息
int x,y;
};
bool bfs(){
queue<point> st; //定义队列
st.push({s1,s2}); //将S点的信息入队
vis[s1][s2]=1; //标记S点为走过
while(!st.empty()){ //当队列不空时
auto p=st.front(); //使p获得队头的信息
st.pop(); //将队头出队
for(int i=0;i<4;i++){ //循环遍历偏移量数组,搜索四个方向
int l=p.x+dx[i],r=p.y+dy[i];
if(l>=1&&l<=n&&r>=1&&r<=m&&!vis[l][r]&&mp[l][r]!='#'){ //判断该点是否满足搜索条件
if(mp[l][r]=='E') return 1; //搜到答案直接返回
vis[l][r]=1; //标记该点已经走过
st.push({l,r}); //将该点入队,后续继续扩展该点搜索
}
}
}
return 0;
}
int main(){
while(cin>>n>>m){
//初始化清空数据
memset(vis,0,sizeof vis);
memset(mp,0,sizeof mp);
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>mp[i][j];
if(mp[i][j]=='S'){ //标记S的坐标
s1=i;
s2=j;
}
}
}
if(bfs()) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
return 0;
}3.1.2 DFS
思想
-
利用递归,将大问题拆分为同类型的小问题解决
-
一般情况下,从初识状态出发,进行扩展得到若干新的状态
-
选定一个状态继续深入,直到不再出现新的状态为止,然后回退,并将上一层的状态恢复
-
重复上述过程,直到将所有可以达到的状态全部遍历
-
一般来说,使用
DFS在提前搜索到答案时一般只进行标记,不提前返回或退出 -
当搜索过程中出现明显不满足目标的状态时可以提前返回,减少搜索次数
例题 3429. 全排列
描述
给定一个由不同的小写字母组成的字符串,输出这个字符串的所有全排列。
我们假设对于小写字母有 a<b<…<y<z,而且给定的字符串中的字母已经按照从小到大的顺序排列。
输入格式
输入只有一行,是一个由不同的小写字母组成的字符串,已知字符串的长度在 1 到 6 之间。
输出格式
输出这个字符串的所有排列方式,每行一个排列。
要求字母序比较小的排列在前面。
字母序如下定义:
已知 S=s1s2…sk,T=t1t2…tk,则 S<T 等价于,存在 p(1≤p≤k),使得 s1=t1,s2=t2,…,sp−1=tp−1,sp<tp 成立。
数据范围
字符串的长度在 1 到 6 之间
输入样例:
abc输出样例:
abc
acb
bac
bca
cab
cba分析
- 对于全排列,我们需要明确排列的顺序,按照字典序排列分析
- 递归处理,每一次递归视为一次选择,递归的层数即为选择数
- 对于每一次的选择进行标记,记录选择并递归到下一层
- 回退时要对上一次的标记的状态进行还原
代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+3;
char a[N]; //存入可选的字符
char ans[N]; //存储当前的排列
bool vis[N]; //记录是否选过了该字符
int n;
void dfs(int u){
if(u==n){ //当选够了全部的字符
for(int i=0;i<n;i++){ //遍历输出排列
cout<<ans[i];
}
cout<<endl;
return ;
}
for(int i=0;i<n;i++){
if(!vis[a[i]]){ //若该字符未曾使用
vis[a[i]]=1; //标记为使用过
ans[u]=a[i]; //选择该字符加入排列
dfs(u+1); //递归到下一层
vis[a[i]]=0; //恢复状态
}
}
}
int main(){
cin>>a; //读入字符数组
n=strlen(a); //得到该字符数组的长度
dfs(0);
return 0;
}例题 843. n-皇后问题
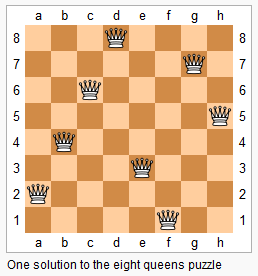
描述
n−皇后问题是指将 n 个皇后放在 n×n 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。
现在给定整数 n,请你输出所有的满足条件的棋子摆法。
输入格式
共一行,包含整数 n。
输出格式
每个解决方案占 n 行,每行输出一个长度为 n 的字符串,用来表示完整的棋盘状态。
其中 . 表示某一个位置的方格状态为空,Q 表示某一个位置的方格上摆着皇后。
每个方案输出完成后,输出一个空行。
注意:输出顺序要按照样例的规律
数据范围
1≤n≤9
输入样例:
4输出样例:
.Q..
...Q
Q...
..Q.
..Q.
Q...
...Q
.Q..分析
- 由于皇后不能互相攻击到,故棋盘的每一行,每一列及其有皇后存在的对角线的平行线上有且只有一个皇后
- 递归处理,每一次递视为一次对棋子的判断,递归的层数视为棋盘的层数,每一层选择放置一个皇后
- 对于递归的每一层,遍历这层棋盘的格子,判断以该格子的列和对角线的平行线上是否存在过皇后
- 若放置皇后,则需要对放置的格子所在的列和对角线的平行线进行标记,并将其记录在答案数组中
- 递归处理上述过程,直到将皇后放置完毕,此时遍历答案数组输出一次排列
- 对于对角线的处理,我们 可以利用数学关系,转换为截距进行标记
代码
#include <bits/stdc++.h>
using namespace std;
const int N=100;
int n;
char mp[N][N]; //当前棋盘的状态
bool y[N],l[N],r[N]; //标记是否存在过皇后
void dfs(int u){
if(u==n+1){ //当u=n+1时说明第n层的棋盘已经放置完毕,输出一次可能性
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
cout<<mp[i][j];
}
cout<<endl;
}
cout<<endl;
return ;
}
for(int i=1;i<=n;i++){
if(!y[i]&&!l[u-i+n]&&!r[u+i+n]){ //若该点所在的列及其所在的对角线的平行线不曾出现过皇后
y[i]=l[u-i+n]=r[u+i+n]=1; //标记
mp[u][i]='Q'; //放置皇后
dfs(u+1); //递归到下一层
mp[u][i]='.'; //回溯
y[i]=l[u-i+n]=r[u+i+n]=0;
}
}
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){ //初始化
for(int j=1;j<=n;j++){
mp[i][j]='.';
}
}
dfs(1);
return 0;
}3.2 树与图的深度优先遍历
思想
- 通过邻接表建图
- 利用
DFS进行遍历
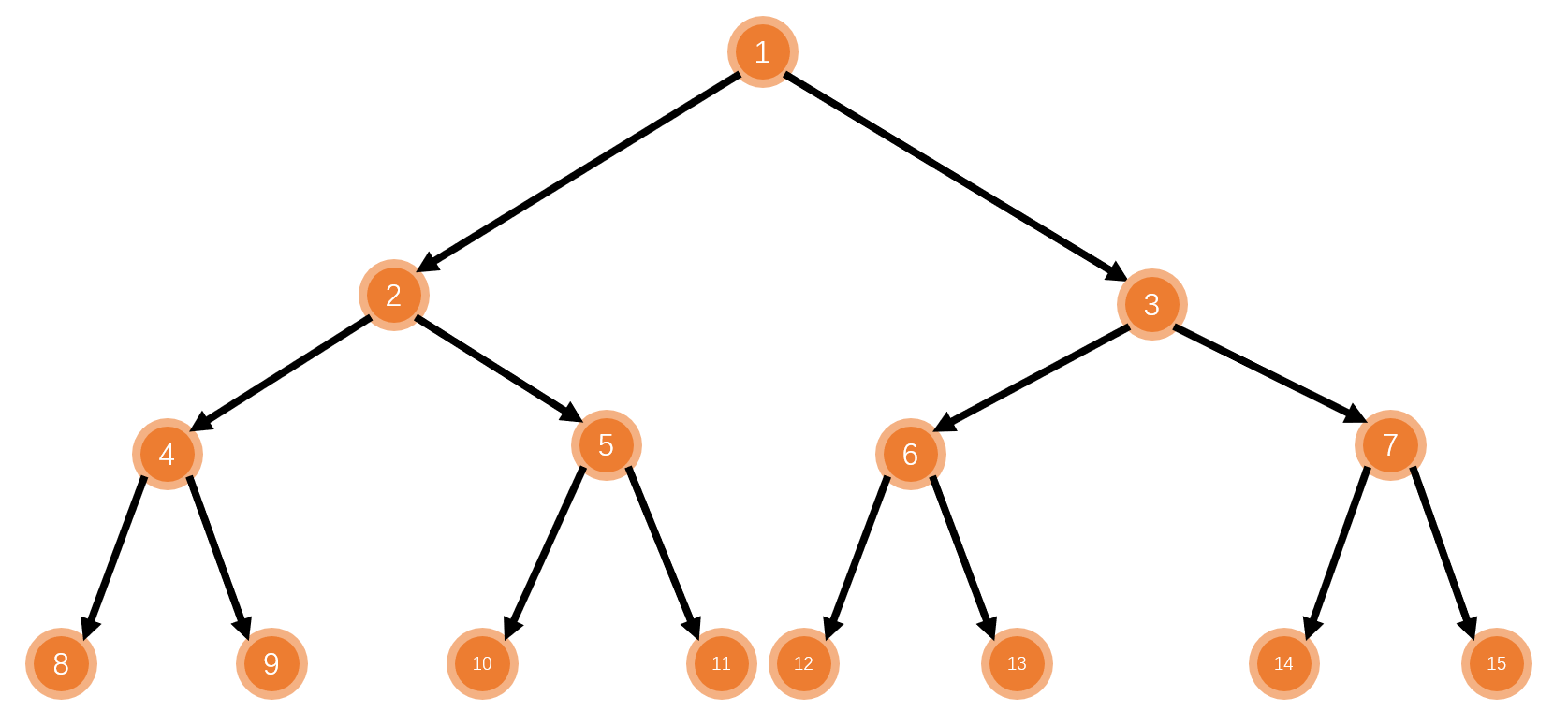
例题 846. 树的重心
描述
给定一颗树,树中包含 n 个结点(编号 1∼n)和 n−1 条无向边。
请你找到树的重心,并输出将重心删除后,剩余各个连通块中点数的最大值。
重心定义:重心是指树中的一个结点,如果将这个点删除后,剩余各个连通块中点数的最大值最小,那么这个节点被称为树的重心。
输入格式
第一行包含整数 n,表示树的结点数。
接下来 n−1 行,每行包含两个整数 a 和 b,表示点 a 和点 b 之间存在一条边。
输出格式
输出一个整数 m,表示将重心删除后,剩余各个连通块中点数的最大值。
数据范围
1≤n≤105
输入样例
9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6输出样例:
4代码
#include <bits/stdc++.h>
using namespace std;
int n;
const int N=1e6+3;
int ans=0x3f3f3f3f;
int h[N],e[N],ne[N],idx; //初始化邻接表
bool vis[N]; //记录是否走过了该节点
void add(int a,int b){
e[idx]=b,ne[idx]=h[a],h[a]=idx++; //建图过程
}
//返回以u为根的子树中节点的数量
int dfs(int u ){
vis[u]=1; //标记走过了该节点
int size=0,sum=1; //size记录子树节点数量的最大值,sum用于记录根子树的个数
for(int i=h[u];i!=-1;i=ne[i]){ //dfs遍历子树结点
if(!vis[e[i]]){
int s=dfs(e[i]);
size=max(size,s);
sum+=s;
}
}
size=max(size,n-sum-1); //n-sum表示的是减掉u为根的子树,整个树剩下的点的数量
ans=min(ans,size); //遍历过的假设重心中,最小的最大联通子图的节点数
return sum;
}
int main(){
memset(h,-1,sizeof h); //初始化邻接表的表头,-1表示尾节点
cin>>n;
for(int i=0;i<n;i++){
int a,b;
cin>>a>>b;
add(a,b),add(b,a); //建立无向图,a->b b->a
}
dfs(1);
cout<<ans<<endl;
return 0;
}3.3 树与图的广度优先遍历
思想
- 通过邻接表建图
- 利用
BFS进行遍历
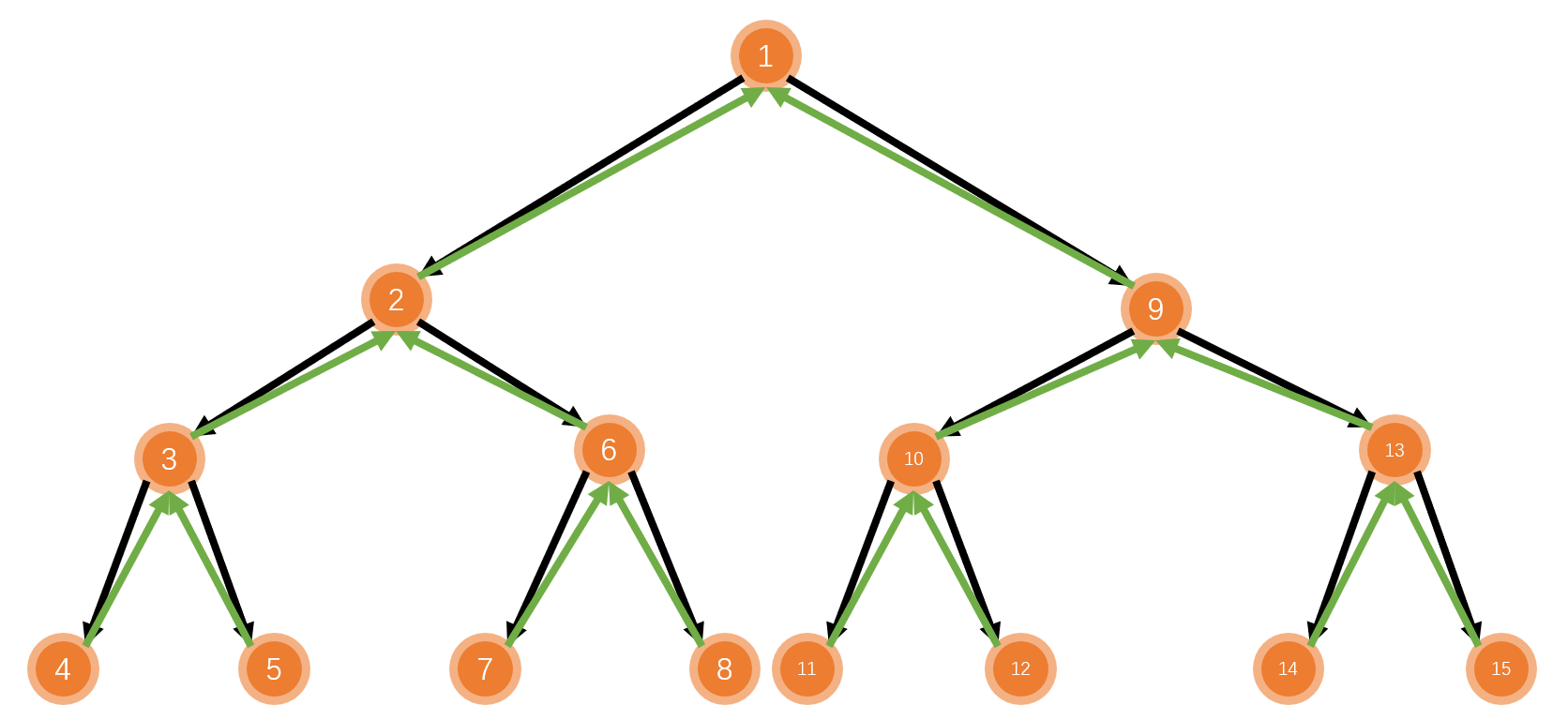
例题 847. 图中点的层次
描述
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环。
所有边的长度都是 1,点的编号为 1∼n。
请你求出 1 号点到 n 号点的最短距离,如果从 1 号点无法走到 n 号点,输出 −1。
输入格式
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含两个整数 a 和 b,表示存在一条从 a 走到 b 的长度为 1 的边。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
数据范围
1≤n,m≤105
输入样例:
4 5
1 2
2 3
3 4
1 3
1 4输出样例:
1代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+3;
int n,m;
int h[N],e[N],ne[N],idx; //初始化邻接表
bool vis[N]; //记录是否走过了该节点
int dist[N]; //记录1号点到n号点的距离
void add(int a,int b){
e[idx]=b,ne[idx]=h[a],h[a]=idx++; //建图过程
}
int bfs(){
memset(dist,-1,sizeof dist); //初始化1号点到n号点的距离全为-1
dist[1]=0; //1号点到1号点的距离为0
queue<int> st; //初始化队列
st.push(1); //1号点入队
vis[1]=1; //标记为走过
while(!st.empty()){
int p=st.front();
st.pop();
for(int i=h[p];i!=-1;i=ne[i]){ //遍历邻接表
if(!vis[e[i]]){
vis[e[i]]=1;
dist[e[i]]=dist[p]+1; //距离+1
st.push(e[i]);
}
}
}
return dist[n];
}
int main(){
memset(h,-1,sizeof h); //初始化邻接表的表头,-1表示尾节点
cin>>n>>m;
for(int i=0;i<m;i++){
int a,b;
cin>>a>>b;
add(a,b); //建立有向图 a->b
}
cout<<bfs()<<endl;
return 0;
}3.4拓扑排序
概念
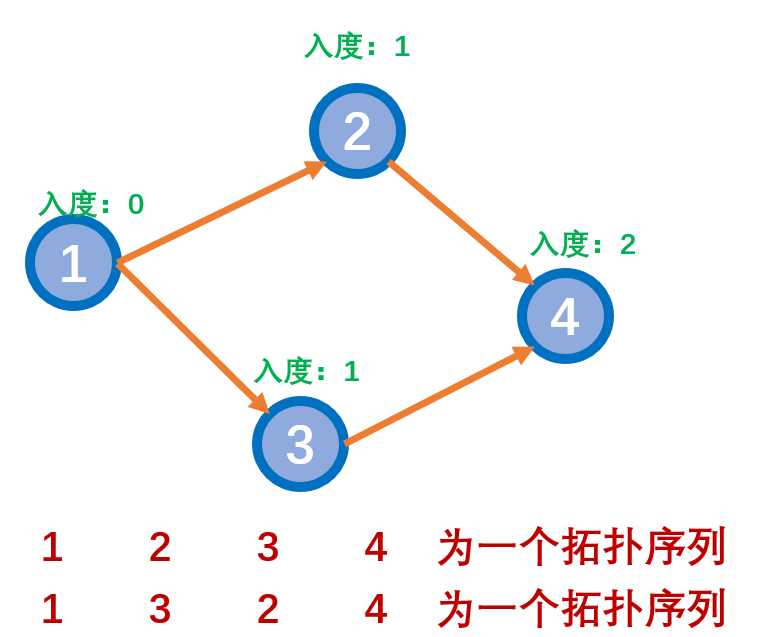
- 拓扑序列是对于有向图而言的,有向图的拓扑序是其顶点的线性排序
- 对于上图,存在4条边:
(1,3)(1,2)(2,4)(2,3) - 该图的拓扑序必须要满足以下两点:
- 每个顶点只出现一次。
- 对于图中的任何一条边,起点必须在终点之前。
判断是否是拓扑序
- 一个有向图,如果图中有入度为 0 的点(没有其他点指向该点),就把这个点删掉,同时也删掉这个点所连的边
- 重复上述处理,如果所有点都能被删掉,则这个图可以进行拓扑排序
以上图为例:
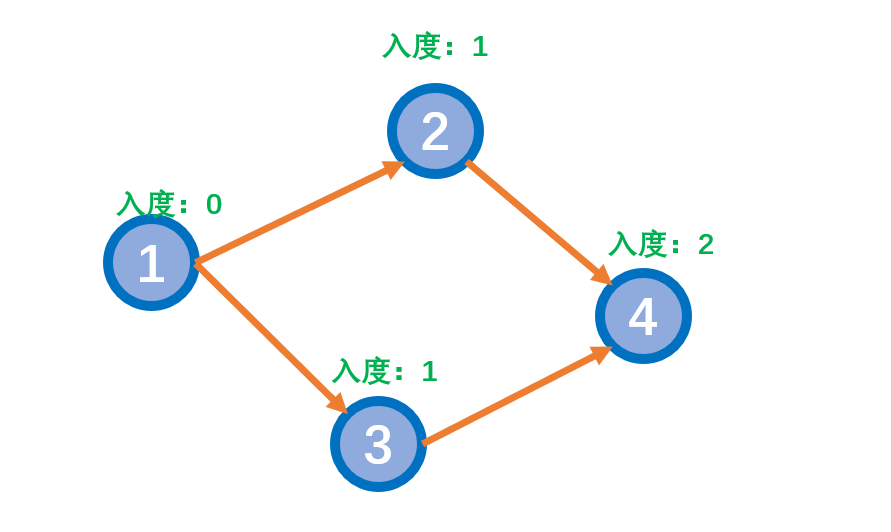
- 初始图为上图的状态,发现1的入度为 0,所以删除1和1上所连的边,结果如下图:
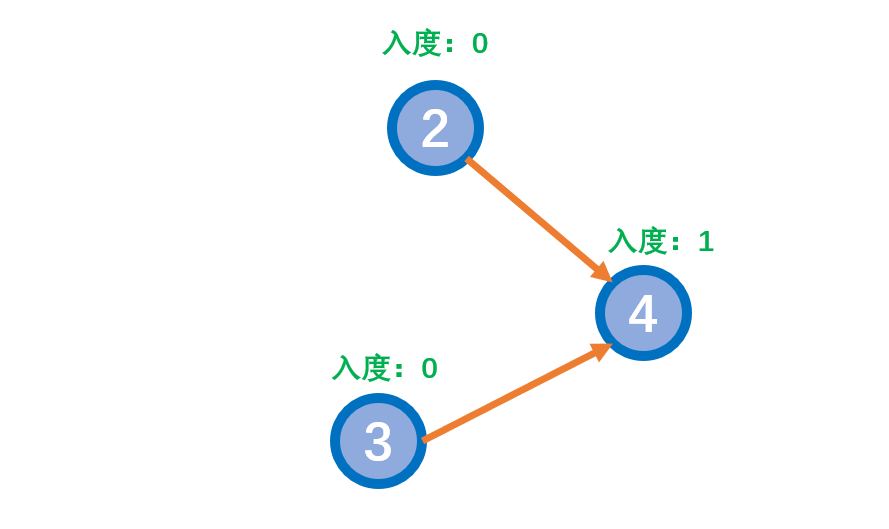
- 此时发现2的入度为 0,3的入度为 0,所以删除2和2上所连的边、3和3上所连的边,结果如下图:
- 此时发现4的入度为 0,且4为最后一个节点,按照删除的顺序可以得到拓扑序
注意:只有有向无环图才有拓扑序,所以有向无环图又被称为拓扑图。
例题 848. 有向图的拓扑序列
描述
给定一个 n 个点 m 条边的有向图,点的编号是 1 到 n,图中可能存在重边和自环。
请输出任意一个该有向图的拓扑序列,如果拓扑序列不存在,则输出 −1。
若一个由图中所有点构成的序列 A 满足:对于图中的每条边 (x,y),x 在 A 中都出现在 y 之前,则称 A 是该图的一个拓扑序列。
输入格式
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含两个整数 x 和 y,表示存在一条从点 x 到点 y 的有向边 (x,y)。
输出格式
共一行,如果存在拓扑序列,则输出任意一个合法的拓扑序列即可。
否则输出 −1。
数据范围
1≤n,m≤105
输入样例:
3 3
1 2
2 3
1 3输出样例:
1 2 3分析
- 首先用邻接表建图,同时记录各个点的入度
- 调用
BFS时将入度为 0 的点放入队列 - 将队列里的点依次出队列,然后找出所有出队列这个点发出的边,删除边,更新被删掉边的节点的入度
- 如果所有点都进过队列,则可以拓扑排序,输出所有顶点。否则输出-1,代表不可以进行拓扑排序
代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+3;
int n,m;
int h[N],e[N],ne[N],idx; //初始化邻接表
int cnt[N]; //记录每个点的入度
queue<int> ans; //记录删掉的节点即为一种答案
void add(int a,int b){
e[idx]=b,ne[idx]=h[a],h[a]=idx++; //建图过程
}
bool bfs(){
queue<int> st; //初始化队列
for(int i=1;i<=n;i++){ //将入度为 0 的点放入队列
if(cnt[i]==0){
st.push(i);
}
}
while(!st.empty()){
int p=st.front();
st.pop();
for(int i=h[p];i!=-1;i=ne[i]){
cnt[e[i]]--; //删掉该边
if(cnt[e[i]]==0){ //删掉边后入度变为0,则将其入队
st.push(e[i]);
}
}
ans.push(p); //将该点记录在答案的顺序中
}
if(ans.size()==n) return 1; //若答案中的点的数量和n相同,说明可以进行拓扑排序
else return 0;
}
int main(){
memset(h,-1,sizeof h);
cin>>n>>m;
for(int i=0;i<m;i++){
int a,b;
cin>>a>>b;
add(a,b);
cnt[b]++;
}
if(bfs()){
while(!ans.empty()){
cout<<ans.front()<<' ';
ans.pop();
}
cout<<endl;
}
else cout<<-1<<endl;
return 0;
}3.5 最短路
3.5.1 Dijkstra
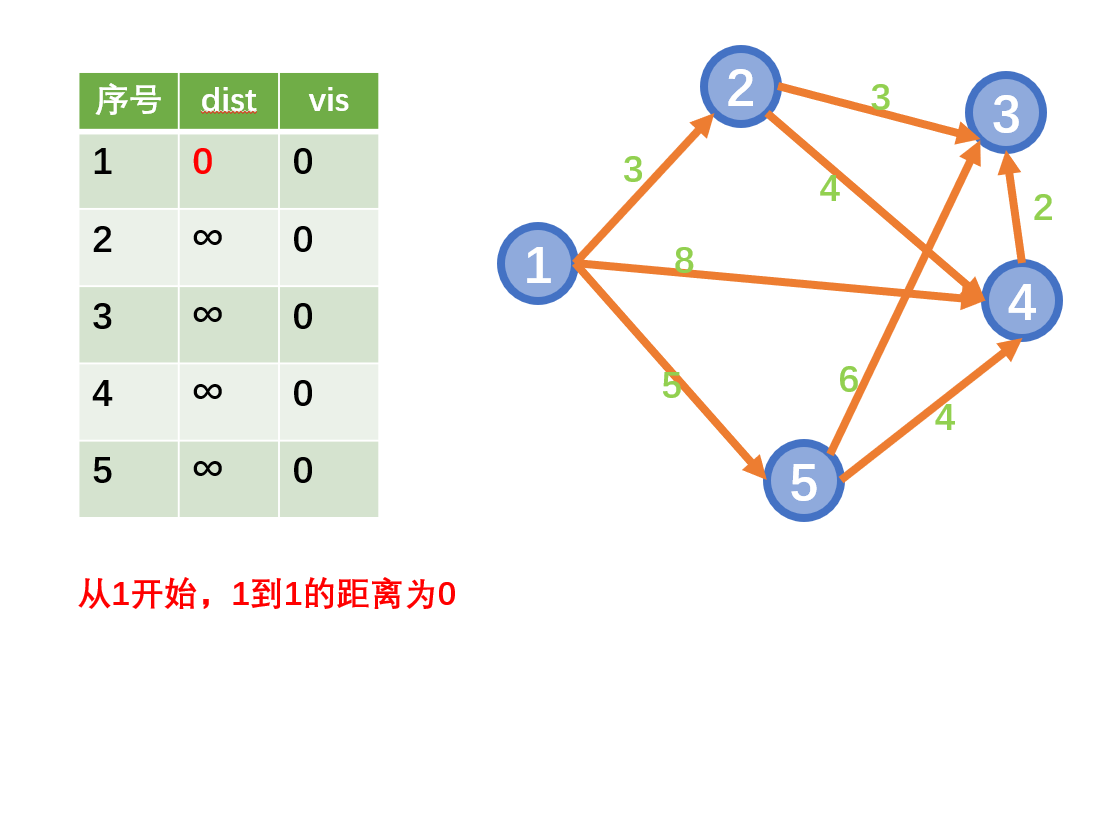
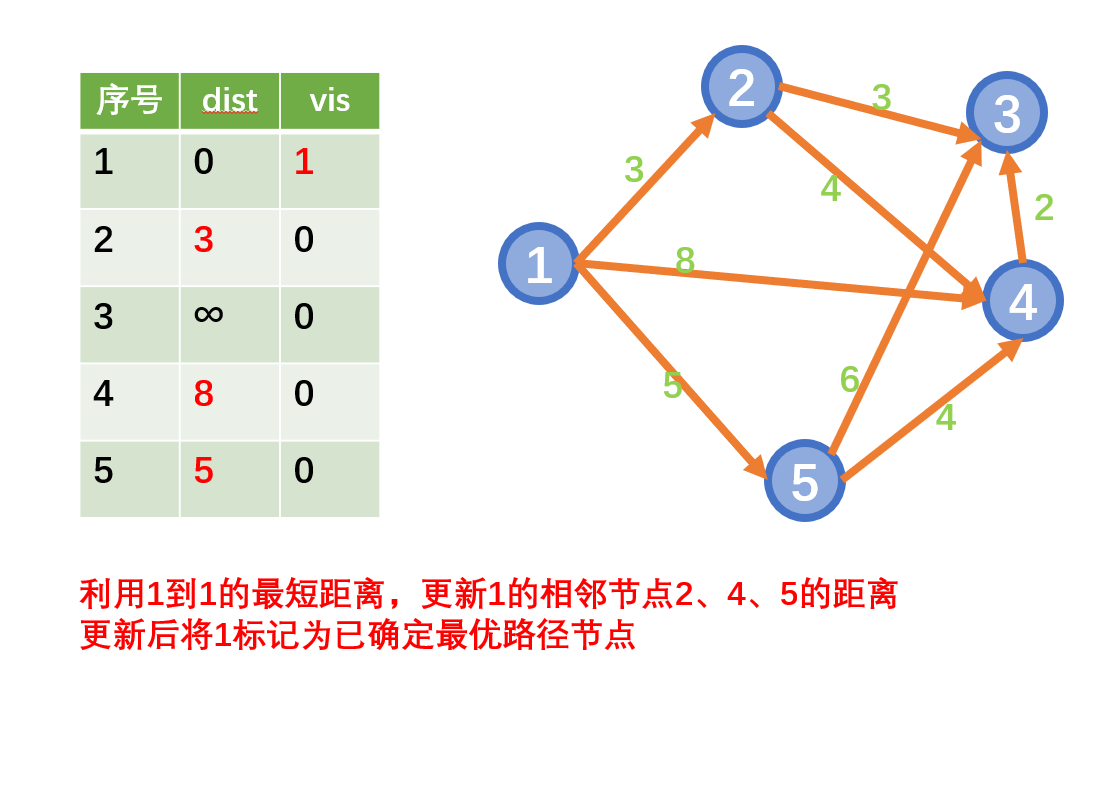
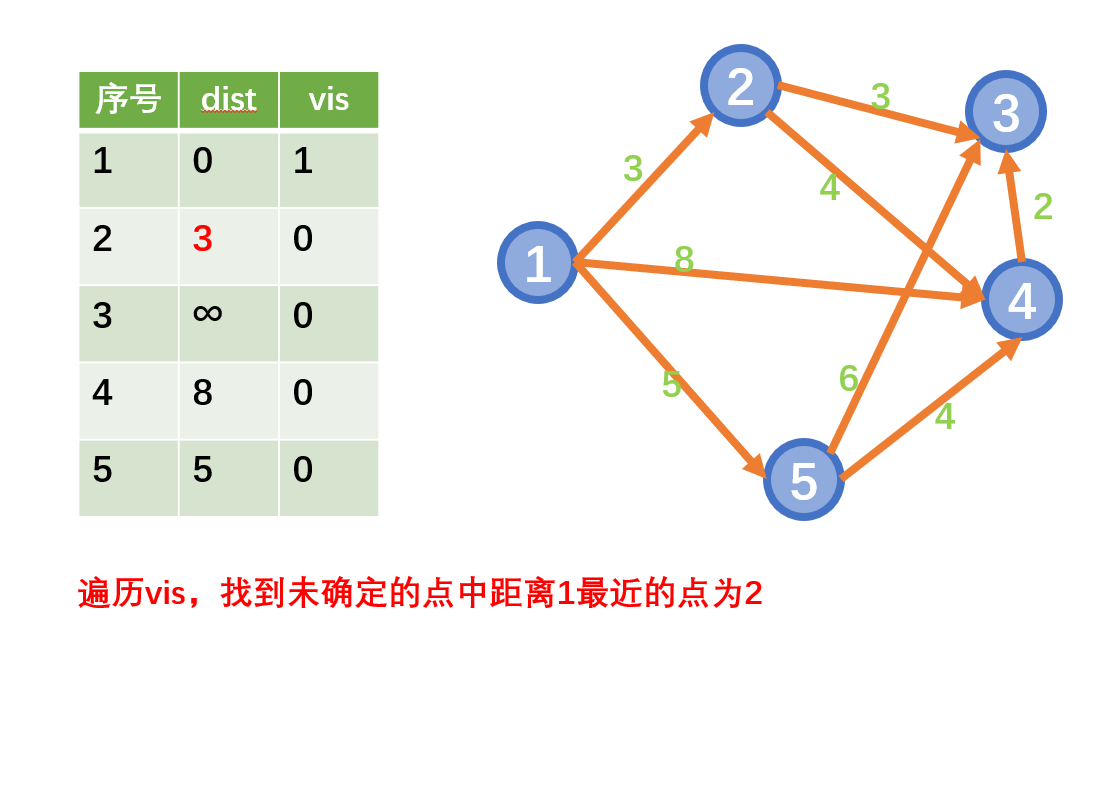
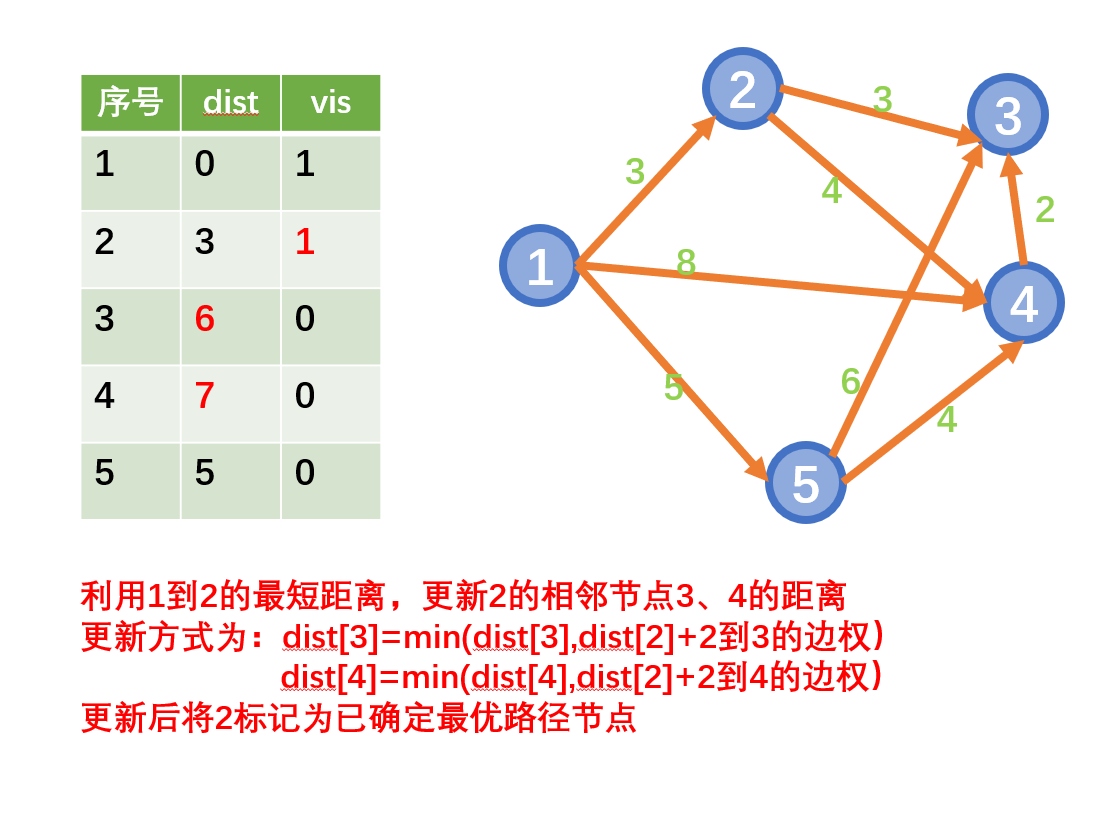
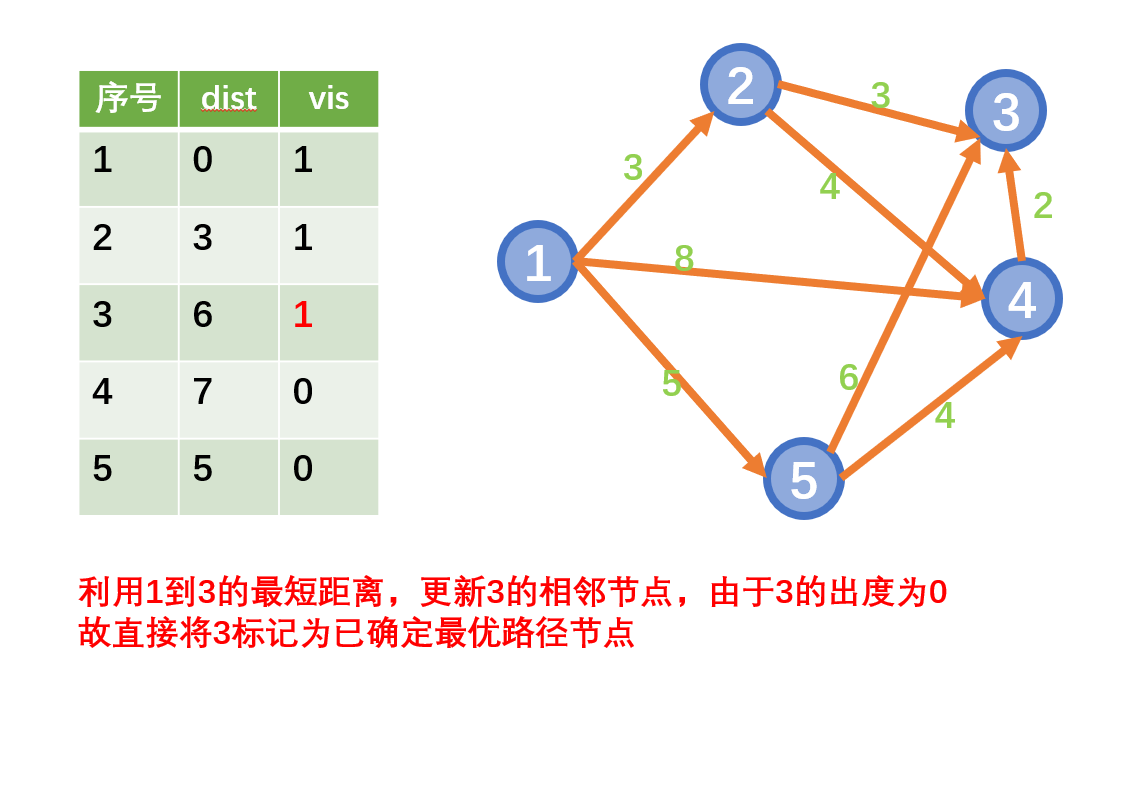
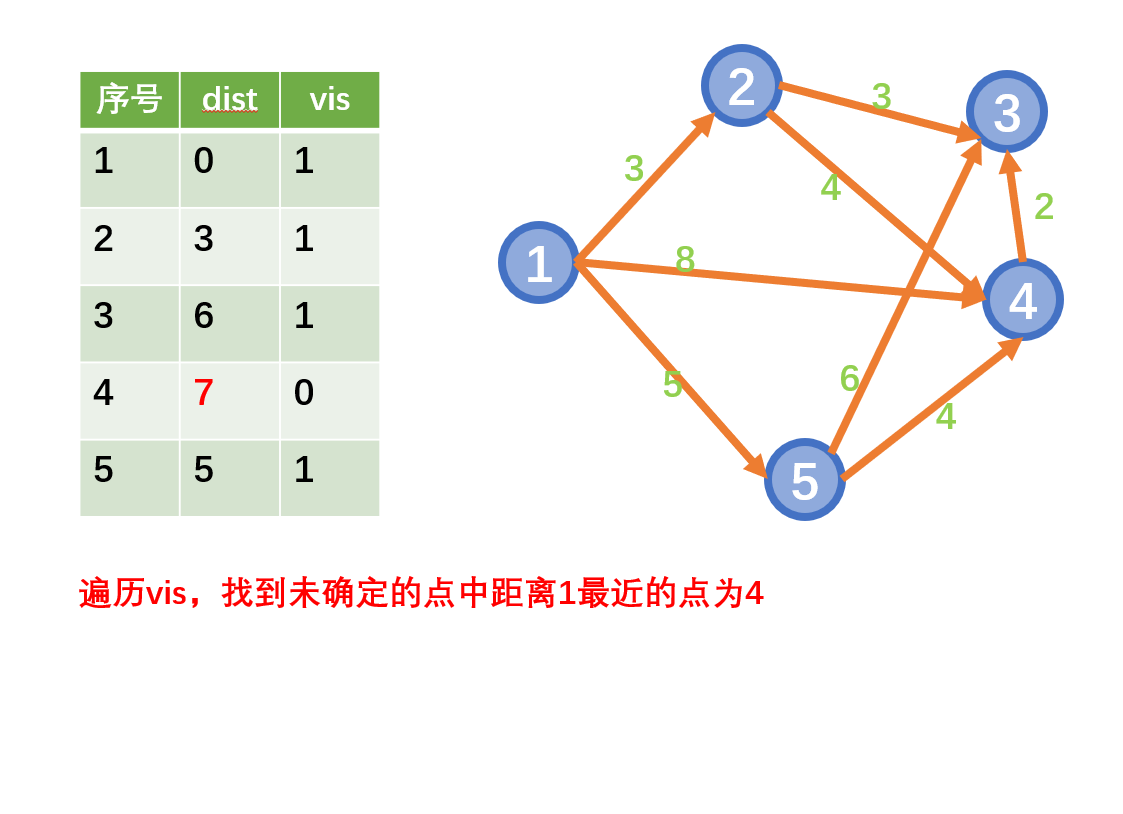
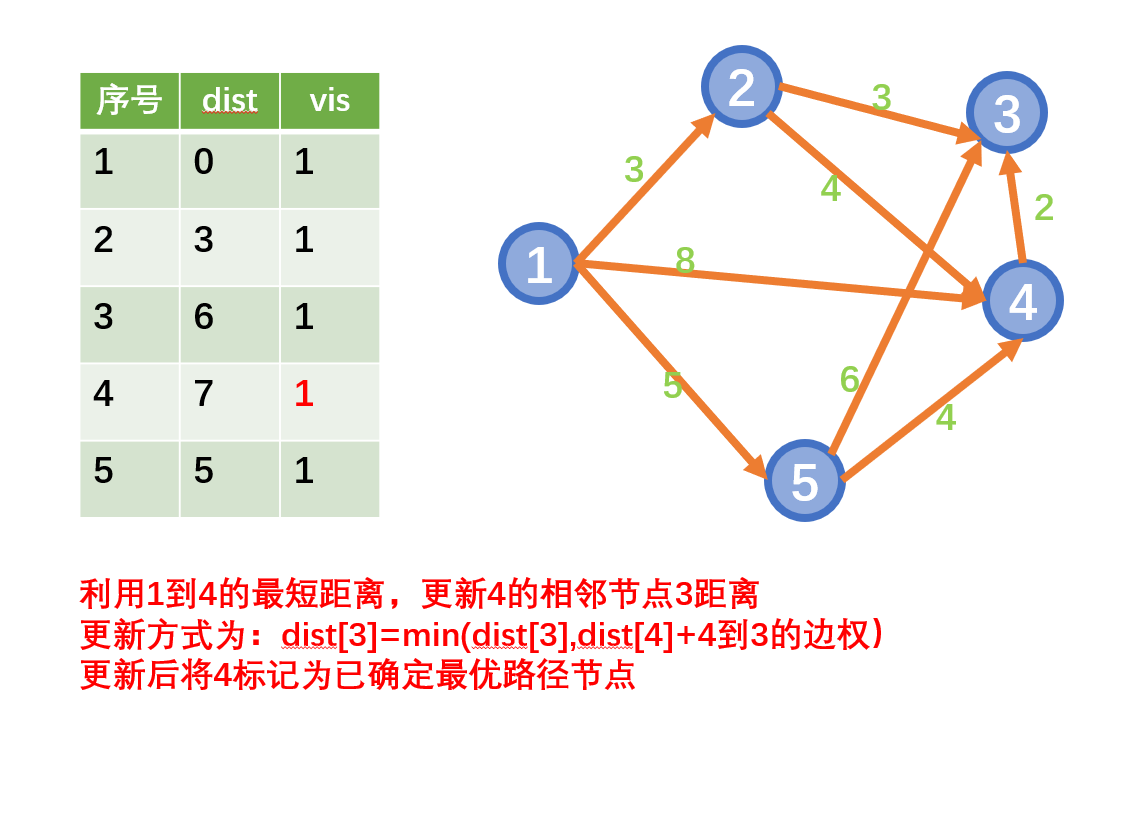
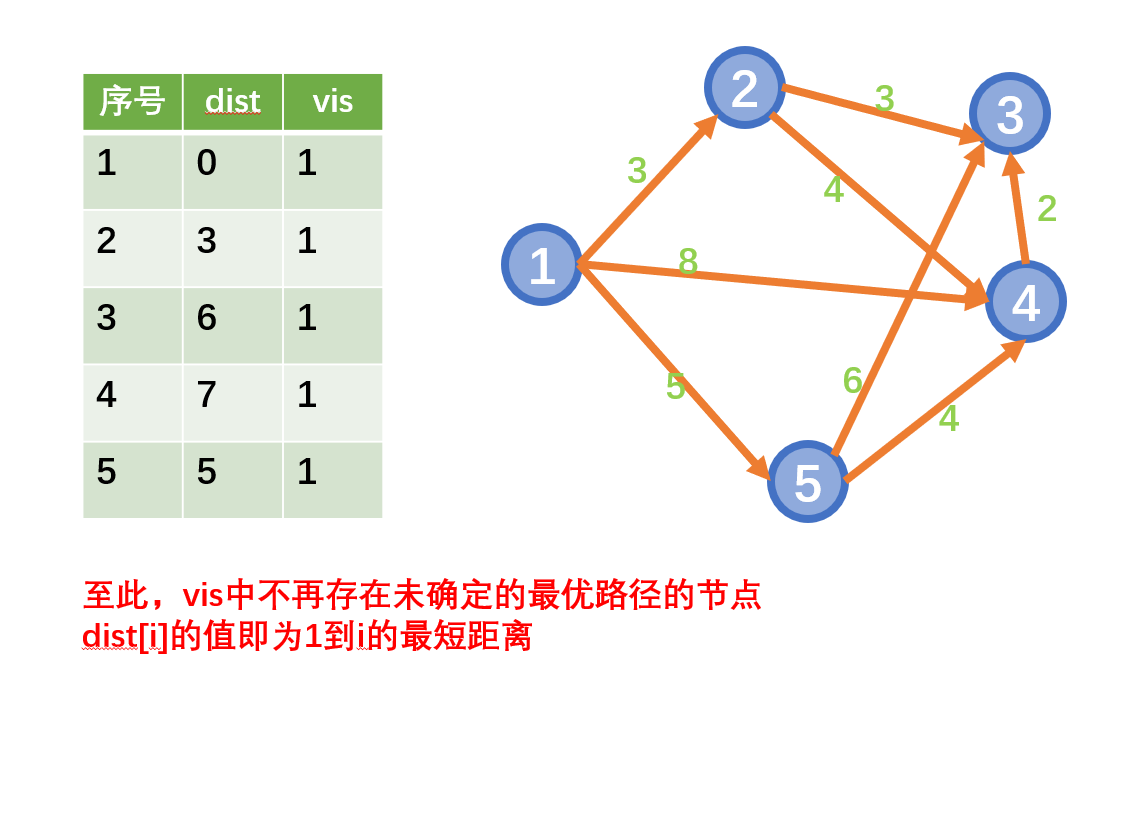
迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959年提出的,因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法(单源最短路)
思想
- 从起始点开始采用贪心策略
- 每一次遍历到始点距离最近且未访问过的顶点的邻接节点,直到扩展到终点为止
注意:Dijkstra不能用于存在负权边的情况
示例:
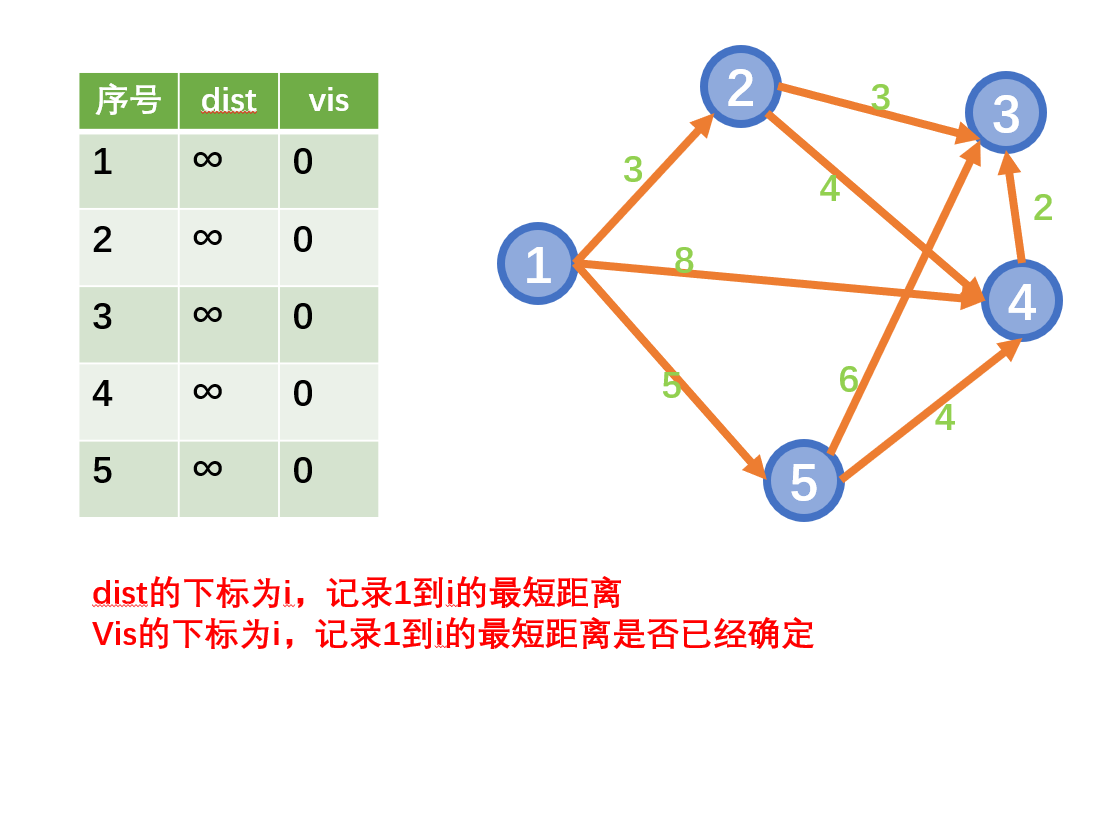



1. 朴素版本(邻接矩阵)
注意
- 当建立的图为稠密图时,用邻接矩阵来建图
模板题 849. Dijkstra求最短路 I
描述
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,所有边权均为正值。
请你求出 1 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 −1。
输入格式
第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
如果路径不存在,则输出 −1。
数据范围
1≤n≤500,
1≤m≤105,
图中涉及边长均不超过10000。
输入样例:
3 3
1 2 2
2 3 1
1 3 4输出样例:
3代码
#include <bits/stdc++.h>
using namespace std;
const int N=510;
int n,m;
int g[N][N]; //初始化邻接矩阵
int dist[N]; //记录最短路径
bool vis[N]; //标记是否已经确定最短路径
int dijkstra(){
memset(dist,0x3f,sizeof dist); //将所有的节点到1号点的初始距离设为INF
dist[1]=0; //1到1的距离为0
for(int i=1;i<=n;i++){
int t=0;
for(int j=1;j<=n;j++){
if(!vis[j]&&dist[j]<dist[t]) t=j; //遍历vis,找到剩余未确定最短路径的点中距离1最近的点
}
for(int j=1;j<=n;j++){
dist[j]=min(dist[j],dist[t]+g[t][j]); //更新1到j的点的距离min(dist[j],dist[t]+t到j的边权)(松弛操作)
}
vis[t]=1; //标记已确定t的最短路径
}
if(dist[n]==0x3f3f3f3f) return -1; //若dist[n]距离1为INF,说明走不到n
else return dist[n];
}
int main(){
memset(g,0x3f,sizeof g); //初始化所有的边权为INF
cin>>n>>m;
for(int i=0;i<m;i++){
int a,b,c;
cin>>a>>b>>c;
g[a][b]=min(g[a][b],c); //将重边的边权更新为最小的那一条
}
cout<<dijkstra()<<endl;
return 0;
}2. 堆优化版本(邻接表)
注意
- 当建立的图为稀疏图时,用邻接表来建图
优化方式
- 利用
priority_queue优化遍历vis找到未确定的最短路径的点中的距离1最近的点的操作
模板题 850. Dijkstra求最短路 II
描述
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,所有边权均为非负值。
请你求出 1 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 −1。
输入格式
第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
如果路径不存在,则输出 −1。
数据范围
1≤n,m≤1.5×105,
图中涉及边长均不小于 0,且不超过 10000。
数据保证:如果最短路存在,则最短路的长度不超过 109。
输入样例:
3 3
1 2 2
2 3 1
1 3 4输出样例:
3代码
#include <bits/stdc++.h>
using namespace std;
typedef pair<int,int> PII;
const int N=1e6+3;
int n,m;
int h[N],e[N],ne[N],w[N],idx; //初始化邻接表
void add(int a,int b,int c){
e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++; //加边操作
}
int dist[N]; //记录最短路径
bool vis[N]; //标记是否已经确定最短路径
int dijkstra(){
memset(dist,0x3f,sizeof dist); //将所有的节点到1号点的初始距离设为INF
dist[1]=0; //1到1的距离为0
priority_queue<PII,vector<PII>,greater<PII>> st; //定义小根堆
st.push({0,1}); //将起始点的信息入队
while(!st.empty()){
auto p=st.top().second;
st.pop();
if(vis[p]) continue; //已确定最短路径的点跳过
for(int i=h[p];i!=-1;i=ne[i]){ //更新相邻的点的最短距离
if(dist[e[i]]>dist[p]+w[i]){ //松弛操作
dist[e[i]]=dist[p]+w[i];
st.push({dist[e[i]],e[i]});
}
}
vis[p]=1; //标记已找到最短路径
}
if(dist[n]==0x3f3f3f3f) return -1;
else return dist[n];
}
int main(){
memset(h,-1,sizeof h); //初始化邻接表的表头
cin>>n>>m;
for(int i=0;i<m;i++){
int a,b,c;
cin>>a>>b>>c;
add(a,b,c);
}
cout<<dijkstra()<<endl;
return 0;
}3.5.2 Bellman-Ford
思想
- 初始化所有点到源点的距离为
INF,把源点到自己的距离设置为0 - 遍历
n次;每次遍历m条边,用每一条边去更新各点到源点的距离
注意
- 需要把
dist数组进行一个备份,防止每次更新的时候出现串联 - 由于存在负权边,因此
return 0的条件就要改成dist[n]>0x3f3f3f3f/2 Bellman_ford算法可以存在负权回路,因为它求得的最短路限制了边数
模板例题 853. 有边数限制的最短路
描述
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环, 边权可能为负数。
请你求出从 1 号点到 n 号点的最多经过 k 条边的最短距离,如果无法从 1 号点走到 n 号点,输出 impossible。
注意:图中可能 存在负权回路 。
输入格式
第一行包含三个整数 n,m,k
接下来 m 行,每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式
输出一个整数,表示从 1 号点到 n 号点的最多经过 k 条边的最短距离。
如果不存在满足条件的路径,则输出 impossible。
数据范围
1≤n,k≤500
1≤m≤10000
任意边长的绝对值不超过 10000
输入样例:
3 3 1
1 2 1
2 3 1
1 3 3输出样例:
3代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+3;
int n,m,k;
int dist[N]; //记录最短路径
int last[N]; //备份dist
struct point{
int a,b,c; //存储边的信息
}p[N];
bool b_f(){
memset(dist,0x3f,sizeof dist); //将所有的节点到1号点的初始距离设为INF
dist[1]=0; //1到1的距离为0
while(k--){ //限制k次
memcpy(last,dist,sizeof dist); //备份dist
for(int i=0;i<m;i++){
auto t=p[i];
dist[t.b]=min(dist[t.b],last[t.a]+t.c); //松弛操作
}
}
if(dist[n]>0x3f3f3f3f/2) return 0;
else return 1;
}
int main(){
cin>>n>>m>>k;
for(int i=0;i<m;i++){
int a,b,c;
cin>>a>>b>>c;
p[i]={a,b,c};
}
if(!b_f()) cout<<"impossible"<<endl;
else cout<<dist[n]<<endl;
return 0;
}3.5.3 SPFA
思想
- 使用队列优化
Bellman-Ford遍历m条边的过程 - 队列存储每次更新了的点,每条边最多遍历一次
- 队头不断出队,计算始点起点经过队头到其他点的距离是否变短,如果变短且被点不在队列中,则把该点加入到队尾
- 重复上述过程,如果存在负权回路,从起点1出发,回到1距离会变小,可以处理负权边和判断负环(抽屉原理)
模板例题
描述
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环, 边权可能为负数。
请你求出 1 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 impossible
数据保证不存在负权回路。
输入格式
第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
如果路径不存在,则输出 impossible。
数据范围
1≤n,m≤105,
图中涉及边长绝对值均不超过 10000。
输入样例:
3 3
1 2 5
2 3 -3
1 3 4输出样例:
2代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+3;
int n,m;
int dist[N]; //记录最短路径
bool vis[N]; ////标该点是不是在队列中
int h[N],e[N],ne[N],w[N],idx; //初始化邻接表
void add(int a,int b,int c){
e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++; //加边操作
}
bool spfa(){
memset(dist,0x3f,sizeof dist); //将所有的节点到1号点的初始距离设为INF
dist[1]=0; //1到1的距离为0
queue<int> st; //定义队列
st.push(1); //将起始点的信息入队
while(!st.empty()){
auto p=st.front();
st.pop();
vis[p]=0; //标记为出队
for(int i=h[p];i!=-1;i=ne[i]){ //遍历相邻的节点
if(dist[e[i]]>dist[p]+w[i]){
dist[e[i]]=dist[p]+w[i]; //松弛操作
if(!vis[e[i]]){ //若该点不在队列中
vis[e[i]]=1;
st.push(e[i]); //入队
}
}
}
}
if(dist[n]==0x3f3f3f3f) return 0;
else return 1;
}
int main(){
memset(h,-1,sizeof h);
cin>>n>>m;
for(int i=0;i<m;i++){
int a,b,c;
cin>>a>>b>>c;
add(a,b,c);
}
if(!spfa()) cout<<"impossible"<<endl;
else cout<<dist[n]<<endl;
return 0;
}例题 852. spfa判断负环
描述
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环, 边权可能为负数。
请你判断图中是否存在负权回路。
输入格式
第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式
如果图中存在负权回路,则输出 Yes,否则输出 No。
数据范围
1≤n≤2000,
1≤m≤10000,
图中涉及边长绝对值均不超过 10000。
输入样例:
3 3
1 2 -1
2 3 4
3 1 -4输出样例:
Yes代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+3;
int n,m;
int dist[N]; //记录最短路径
int cnt[N]; //记录入队的次数
bool vis[N]; ////标该点是不是在队列中
int h[N],e[N],ne[N],w[N],idx; //初始化邻接表
void add(int a,int b,int c){
e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++; //加边操作
}
bool spfa(){
memset(dist,0x3f,sizeof dist); //将所有的节点到1号点的初始距离设为INF
dist[1]=0; //1到1的距离为0
queue<int> st; //定义队列
//点1可能到不了有负环的点, 因此把所有点都加入队列
for(int i=1;i<=n;i++){
st.push(i);
vis[i]=1;
}
while(!st.empty()){
auto p=st.front();
st.pop();
vis[p]=0;
for(int i=h[p];i!=-1;i=ne[i]){
if(dist[e[i]]>dist[p]+w[i]){
cnt[e[i]]=cnt[p]+1;
if(cnt[e[i]]>=n) return 0; //入队大于等于n次说明存在负环
dist[e[i]]=dist[p]+w[i];
if(!vis[e[i]]){
vis[e[i]]=1;
st.push(e[i]);
}
}
}
}
return 1;
}
int main(){
memset(h,-1,sizeof h);
cin>>n>>m;
for(int i=0;i<m;i++){
int a,b,c;
cin>>a>>b>>c;
add(a,b,c);
}
if(!spfa()) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
return 0;
}3.5.4 Floyd
思想
f[k,i,j]表示从i走到j的路径上除i和j点外只经过1到k的点的所有路径的最短距离。那么f[k,i,j] = min(f[k-1,i,j] , f[k-1,i,k] + f[k-1,k,j]),因此在计算第k层的f[i, j]的时候必须先将第k - 1层的所有状态计算出来,所以需要把k放在最外层- 读入邻接矩阵,将次通过动态规划转换为从
i到j的最短距离矩阵 - 判断从
a到b是否是无穷大距离时,需要进行if(t > INF/2)判断,而并非是if(t == INF)判断,原因是INF是一个确定的值,并非真正的无穷大,会随着其他数值而受到影响,t大于某个与INF相同数量级的数即可
注意:Floyd 用于求多源汇最短路,时间复杂度为O(n^3)
模板例题 854. Floyd求最短路
描述
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,边权可能为负数。
再给定 k 个询问,每个询问包含两个整数 x 和 y,表示查询从点 x 到点 y 的最短距离,如果路径不存在,则输出 impossible。
数据保证图中不存在负权回路。
输入格式
第一行包含三个整数 n,m,k。
接下来 m 行,每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
接下来 k 行,每行包含两个整数 x,y,表示询问点 x 到点 y 的最短距离。
输出格式
共 k 行,每行输出一个整数,表示询问的结果,若询问两点间不存在路径,则输出 impossible。
数据范围
1≤n≤200,
1≤k≤n2
1≤m≤20000,
图中涉及边长绝对值均不超过 10000。
3 3 2
1 2 1
2 3 2
1 3 1
2 1
1 3输出样例:
输出样例:
impossible
1代码
#include <bits/stdc++.h>
using namespace std;
const int N=510;
int dist[N][N]; //记录答案
int n,m,k;
void floyd(){
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
dist[i][j]=min(dist[i][j],dist[i][k]+dist[k][j]); //更新最短路径
}
}
}
}
int main(){
cin>>n>>m>>k;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(i!=j) dist[i][j]=0x3f3f3f3f;
}
}
for(int i=0;i<m;i++){
int a,b,c;
cin>>a>>b>>c;
dist[a][b]=min(dist[a][b],c);
}
floyd();
while(k--){
int a,b;
cin>>a>>b;
if(dist[a][b]>0x3f3f3f3f/2) cout<<"impossible"<<endl;
else cout<<dist[a][b]<<endl;
}
return 0;
}3.6 最小生成树
概念
- 最小生成树(minimum spanning tree)是由n个顶点,n-1条边,将一个连通图连接起来,且使权值最小的结构
- 最小生成树可以用
Prim算法或Kruskal算法求出
3.6.1 Prim
思想
- 类似于
Dijkstra采用贪心策略 - 维护一个集合,每次更新集合外的点到集合中任意点的最短距离
- 将该点加入集合,重复操作,直到所有的点都在集合当中
朴素
Prim算法适用于稠密图的情况,稀疏图可以使用堆进行优化,方法同Dijkstra的优化
模板例题 858. Prim算法求最小生成树
描述
给定一个 n 个点 m 条边的无向图,图中可能存在重边和自环,边权可能为负数。
求最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
给定一张边带权的无向图 G=(V,E),其中 V 表示图中点的集合,E 表示图中边的集合,n=|V|,m=|E|。
由 V 中的全部 n 个顶点和 E 中 n−1 条边构成的无向连通子图被称为 G 的一棵生成树,其中边的权值之和最小的生成树被称为无向图 G 的最小生成树。
输入格式
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含三个整数 u,v,w,表示点 u 和点 v 之间存在一条权值为 w 的边。
输出格式
共一行,若存在最小生成树,则输出一个整数,表示最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
数据范围
1≤n≤500,
1≤m≤105,
图中涉及边的边权的绝对值均不超过 10000。
输入样例:
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4输出样例:
6代码
#include <bits/stdc++.h>
using namespace std;
const int N=510;
int n,m;
int g[N][N]; //稠密图使用邻接矩阵存储
int dist[N]; //到集合的最短距离
bool vis[N]; //维护的当前生成树中的点的集合
int res; //最小生成树边的总长
int prim(){
memset(dist,0x3f,sizeof dist); //初始化距离为0x3f3f3f3f
for(int i=0;i<n;i++){
int t=-1;
for(int j=1;j<=n;j++){
if(!vis[j]&&(t==-1||dist[t]>dist[j])) t=j; //遍历vis,找到集合外距离集合最近的点
}
if(i&&dist[t]==0x3f3f3f3f) return dist[t]; //若距离集合为INF说明没有最小生成树
if(i) res+=dist[t];
for(int j=1;j<=n;j++){
dist[j]=min(dist[j],g[t][j]); //更新其他点到集合的最短距离
}
vis[t]=1; //标记为存在集合中
}
return res;
}
int main(){
cin>>n>>m;
memset(g,0x3f,sizeof g);
for(int i=0;i<m;i++){
int a,b,c;
cin>>a>>b>>c;
g[a][b]=g[b][a]=min(g[a][b],c); //建立无向图,重边取最小
}
int p=prim();
if(p==0x3f3f3f3f) cout<<"impossible"<<endl;
else cout<<p<<endl;
return 0;
}3.6.2 Kruskal
思想
- 先对所有的边按照边权从小到大进行排序
- 遍历排序后的所有边,用并查集来维护最小生成树的集合
- 若两个点不在同一集合中,则合并两个集合
- 重复操作,直到所有的连通块合并,最终的集合为最小生成树的集合
模板例题 859. Kruskal算法求最小生成树
描述
给定一个 n 个点 m 条边的无向图,图中可能存在重边和自环,边权可能为负数。
求最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
给定一张边带权的无向图 G=(V,E),其中 V 表示图中点的集合,E 表示图中边的集合,n=|V|,m=|E|。
由 V 中的全部 n 个顶点和 E 中 n−1 条边构成的无向连通子图被称为 G 的一棵生成树,其中边的权值之和最小的生成树被称为无向图 G 的最小生成树。
输入格式
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含三个整数 u,v,w,表示点 u 和点 v 之间存在一条权值为 w 的边。
输出格式
共一行,若存在最小生成树,则输出一个整数,表示最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
数据范围
1≤n≤105,
1≤m≤2∗105,
图中涉及边的边权的绝对值均不超过 1000。
输入样例:
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4输出样例:
6代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+3;
int n,m;
int p[N]; //并查集来维护连通块
int ans,cnt; //ans为当前生成树的总边权,cnt为当前生成树边的数量
struct point{ //记录边的信息
int x,y,z;
bool operator<(const point &p)const{ //重载小于号
return z<p.z;
}
}g[N];
int find(int x){ //并查集查询操作
if(p[x]!=x) p[x]=find(p[x]);
return p[x];
}
int kruskal(){
sort(g,g+m); //先对边权进行排序
for(int i=1;i<=n;i++) p[i]=i; //初始化并查集
for(int i=0;i<m;i++){ //枚举m条边
int a=g[i].x,b=g[i].y,c=g[i].z;
a=find(a),b=find(b);
if(a!=b){ //如果a和b不在同一个集合中
p[a]=b; //合并a和b
ans+=c; //更新总边权
cnt++; //总边数加一
}
}
if(cnt!=n-1) return 0x3f3f3f3f; //总边数!=n-1说明没有最小生成树
else return ans;
}
int main(){
cin>>n>>m;
for(int i=0;i<m;i++){
int a,b,c;
cin>>a>>b>>c;
g[i]={a,b,c};
}
if(kruskal()==0x3f3f3f3f) cout<<"impossible"<<endl;
else cout<<ans<<endl;
return 0;
}3.7 二分图
概念
- 将图的点分配到两个集合中,使得图的每一条边相连的两个点不在同一集合中
- 即图中的点可以分成左右两部分,左侧的点只和右侧的点相连,右侧的点只和左侧的点相连
注意:若改图存在奇数环(构成环的点有奇数个)则无法生成二分图
示例:
3.7.1 染色法判断二分图
思想
- 首先在图中选择任意一点开始染色
- 判断其相邻的顶点中,若未染色则将其染上和相邻顶点不同的颜色
- 若已经染色且颜色和相邻顶点的颜色相同则说明不是二分图,若颜色不同则继续判断
- 可以使用
DFS或BFS实现
模板例题 860. 染色法判定二分图
描述
给定一个 n 个点 m 条边的无向图,图中可能存在重边和自环。
请你判断这个图是否是二分图。
输入格式
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含两个整数 u 和 v,表示点 u 和点 v 之间存在一条边。
输出格式
如果给定图是二分图,则输出 Yes,否则输出 No。
数据范围
1≤n,m≤105
输入样例:
4 4
1 3
1 4
2 3
2 4输出样例:
Yes代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+3;
int n,m;
int h[N],e[N],ne[N],idx; //初始化邻接表
int vis[N]; //标记染的颜色
void add(int a,int b){
e[idx]=b,ne[idx]=h[a],h[a]=idx++; //加边操作
}
int flag=1; //标记是否可以生成二分图
bool dfs(int u,int c){
vis[u]=c; //将该点染色
for(int i=h[u];i!=-1;i=ne[i]){ //遍历该点的相邻点
if(!vis[e[i]]){ //若该点未染色
if(!dfs(e[i],3-c)) return 0; //染色为2,若递归染色结果为false说明无法生成二分图
}
else if(vis[e[i]]==c) return 0; //若该点已经染色,判断该点颜色是否相同,相同说明无法生成二分图
}
return 1;
}
int main(){
memset(h,-1,sizeof h);
cin>>n>>m;
for(int i=0;i<m;i++){
int a,b;
cin>>a>>b;
add(a,b),add(b,a); //建立无向图
}
for(int i=1;i<=n;i++){
if(!vis[i]){ //若该点未染色
if(!dfs(i,1)){ //若染色为1
flag=0; //若递归染色结果为false,标记为无法生成二分图
break;
}
}
}
if(flag) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
return 0;
}3.7.2 匈牙利算法
概念
- 匹配:在二分图中,任意两条边都没有公共顶点(一对一)的一组边称为一组匹配
- 最大匹配:一个图所有匹配中,所含匹配的边数最多的匹配,称为这个图的最大匹
思想
- 基于Hall定理中充分性证明的思想
- 核心是寻找增广路径,用增广路径求二分图最大匹配
模板例题 861. 二分图的最大匹配
描述
给定一个二分图,其中左半部包含 n1 个点(编号 1∼n1),右半部包含 n2 个点(编号 1∼n2),二分图共包含 m 条边。
数据保证任意一条边的两个端点都不可能在同一部分中。
请你求出二分图的最大匹配数。
二分图的匹配:给定一个二分图 G,在 G 的一个子图 M 中,M 的边集 {E} 中的任意两条边都不依附于同一个顶点,则称 M 是一个匹配。
二分图的最大匹配:所有匹配中包含边数最多的一组匹配被称为二分图的最大匹配,其边数即为最大匹配数。
输入格式
第一行包含三个整数 n1、 n2 和 m。
接下来 m 行,每行包含两个整数 u 和 v,表示左半部点集中的点 u 和右半部点集中的点 v 之间存在一条边。
输出格式
输出一个整数,表示二分图的最大匹配数。
数据范围
1≤n1,n2≤500,
1≤u≤n1,
1≤v≤n2,
1≤m≤105
输入样例:
2 2 4
1 1
1 2
2 1
2 2输出样例:
2代码
#include <bits/stdc++.h>
using namespace std;
int n1,n2,m;
int res;
const int N=1e6+3;
int match[N]; //记录当前配对的信息
bool vis[N]; //标记当前匹配阶段是否发生过配对
int h[N],e[N],ne[N],idx; //初始化邻接表,存稀疏图
void add(int a,int b){
e[idx]=b,ne[idx]=h[a],h[a]=idx++; //加边操作
}
bool find(int u){ //判断是否可以配对
for(int i=h[u];i!=-1;i=ne[i]){ //遍历该点的所有相邻点
if(!vis[e[i]]){ //若在该次模拟中,该点尚未被匹配
vis[e[i]]=1; //标记为匹配
if(match[e[i]]==0||find(match[e[i]])){ //若该点最终没有配对,或原来的配对的点可以找到其他新的配对
match[e[i]]=u; //更新匹配的状态
return 1; //匹配成功
}
}
}
return 0;
}
int main(){
memset(h,-1,sizeof h);
cin>>n1>>n2>>m;
for(int i=0;i<m;i++){
int a,b;
cin>>a>>b;
add(a,b);
}
for(int i=1;i<=n1;i++){
memset(vis,0,sizeof vis); //每次模拟匹配,需要初始化
if(find(i)) res++;
}
cout<<res<<endl;
}