2022_HAUE_计算机学院暑期培训——BFS&DFS
1. 预习内容
1.1 阅读资料
1.2 练习题目
1. Z字形扫描
描述
在图像编码的算法中,需要将一个给定的方形矩阵进行 Z 字形扫描(Zigzag Scan)。
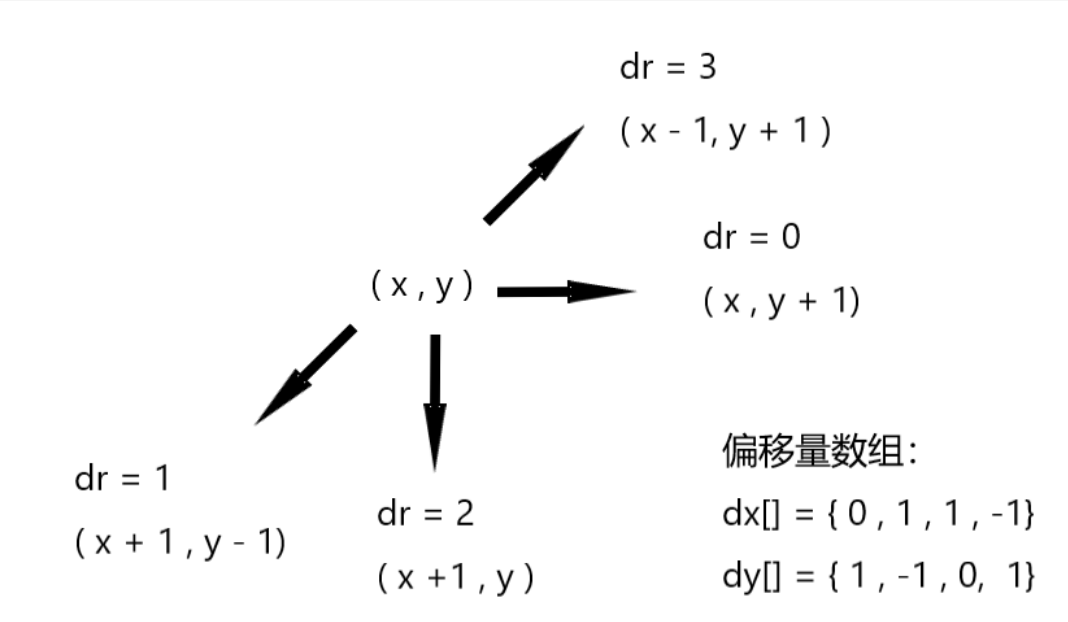
给定一个 n×n 的矩阵,Z 字形扫描的过程如下图所示:
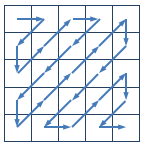
对于下面的 4×4 的矩阵,
1 5 3 9
3 7 5 6
9 4 6 4
7 3 1 3对其进行 Z 字形扫描后得到长度为 16 的序列:1 5 3 9 7 3 9 5 4 7 3 6 6 4 1 3。
请实现一个 Z 字形扫描的程序,给定一个 n×n 的矩阵,输出对这个矩阵进行 Z 字形扫描的结果。
输入格式
输入的第一行包含一个整数 nn,表示矩阵的大小。
输入的第二行到第 n+1n+1 行每行包含 nn 个正整数,由空格分隔,表示给定的矩阵。
输出格式
输出一行,包含 n×n 个整数,由空格分隔,表示输入的矩阵经过 ZZ 字形扫描后的结果。
数据范围
1≤n≤500,
矩阵元素为不超过 1000 的正整数。
输入样例:
4
1 5 3 9
3 7 5 6
9 4 6 4
7 3 1 3输出样例:
1 5 3 9 7 3 9 5 4 7 3 6 6 4 1 3分析
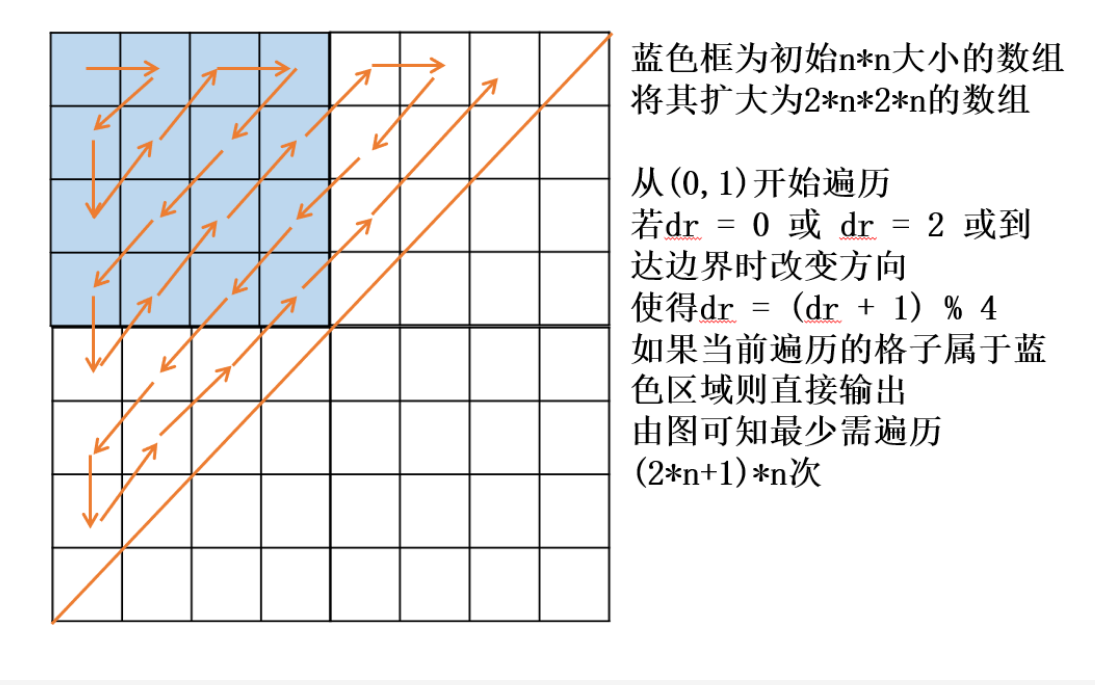
- 该题以Z字形遍历数组,对于奇数和偶数情况下,边界转向复杂
- 扩大原二维数组,使边界转向统一
- 观察旋转方向,设初始方向
dr = 0 - 扩大二维数组,遍历满足在原数组范围内时输出
代码
#include <bits/stdc++.h>
using namespace std;
const int N=505;
int a[2*N][2*N]; //定义时直接扩大
int main(){
int n;
scanf("%d",&n);
for(int i=0;i<n;i++){ //初始化二维数组
for(int j=0;j<n;j++){
scanf("%d",&a[i][j]);
}
}
int dr=0,dx[]={0,1,1,-1},dy[]={1,-1,0,1}; //定义(0,1)的方向dr=0 定义偏移量数组
printf("%d ",a[0][0]); //先将(0,0)位置的数输出
int x=0,y=1; //初始化位置为(0,1)
for(int i=0;i<(2*n+1)*n;i++){ //循环遍历扩大后的数组
if(x<n&&y<n){
printf("%d ",a[x][y]); //满足在原始数组范围内输出
}
int l=x+dx[dr],r=y+dy[dr]; //临时变量判断下一个要遍历的格子坐标(l,r)
if(dr==0||dr==2||r<0||l<0||r>=n||l>=n){ //如果dr=0或dr=2或(l,r)出界时改变方向
dr=(dr+1)%4;
l=x+dx[dr],r=y+dy[dr];
}
x=l,y=r; //更新(x,y)
}
return 0;
}2. 上楼梯
描述
一个楼梯共有 n 级台阶,每次可以走一级或者两级或者三级,问从第 0 级台阶走到第 n 级台阶一共有多少种方案。
输入格式
一个整数 N。
输出格式
一个整数,表示方案总数。
数据范围
1≤N≤20
输入样例:
4输出样例:
7分析
- 利用递归进行模拟
代码
#include <bits/stdc++.h>
using namespace std;
int n,ans;
void dfs(int u){
if(u==n) ans++;
//当不会超出n时进行下一步
if(u+1<=n) dfs(u+1);
if(u+2<=n) dfs(u+2);
if(u+3<=n) dfs(u+3);
}
int main(){
cin>>n;
dfs(0);
cout<<ans<<endl;
return 0;
}2. 课程内容
2.1 搜索技术简介
搜索是基本的编程技术,在算法竞赛学习中是基础的基础。
分类
- DFS
- BFS
- A* (BFS+贪心)
- 双向广搜
- 双端队列广搜
- 双向DFS
- IDDFS (DFS+BFS)
- IDA* (IDDFS优化)
搜索常使用的算法是BFS和DFS,BFS用队列、DFS用递归来具体实现。在BFS和DFS的基础上可以扩展出A*算法、双向广搜算法、迭代加深搜索、IDA等技术。
思想
- 搜索技术是“暴力法”算法思想的具体实现
- 将所有可能的情况都罗列出来,然后逐一检查,从中找到答案
特点
- 很多问题只能用暴力法解决,例如猜密码,走迷宫等问题
- 对于小规模的问题,暴力法完全够用,而且避免了高级算法需要的复杂编码
- 把暴力法当作参照(benchmark)。拿到题目后,如果没有其他思路,可以先试试暴力法,在具体编程时常常需要对暴力法进行优化,以减少搜索空间,提高效率。
2.2 BFS (广度优先搜索)
2.2.1 C++STL队列相关操作
特点
- 先进先出
- 只允许对队头进行操作

1. 头文件
#include <queue>
2. 定义与声明
queue<数据类型> 名称
eg:
#include <iostream>
#include <string>
#include <queue>
using namespace std;
struct point{ //声明point为struct类型
int x,y;
};
int main() {
queue<int> a; //定义一个名为a,存储int类型数据的队列
queue<string> b; //定义一个名为b,存储string类型数据的队列
queue<point> c; //定义一个名为c,存储point类型数据的队列
return 0;
}3. 向队尾插入元素(入队)
语法:.push()
eg:
#include <iostream>
#include <string>
#include <queue>
using namespace std;
struct point{ //声明point为struct类型
int x,y;
};
int main() {
queue<int> a; //定义一个名为a,存储int类型数据的队列
queue<string> b; //定义一个名为b,存储string类型数据的队列
queue<point> c; //定义一个名为c,存储point类型数据的队列
a.push(1); //在队列a的末尾添加int类型的元素1
b.push("abc"); //在队列b的末尾添加string类型的元素abc
point p;
p.x=10;
p.y=20;
c.push(p); //在队列c的末尾添加point类型的元素p,p.x=10,p.y=20
c.push({10,20}); //与c.push(p)等价
return 0;
}4. 将队头弹出(出队)
语法:.pop()
eg:
#include <iostream>
#include <string>
#include <queue>
using namespace std;
struct point{ //声明point为struct类型
int x,y;
};
int main() {
queue<int> a; //定义一个名为a,存储int类型数据的队列
queue<string> b; //定义一个名为b,存储string类型数据的队列
queue<point> c; //定义一个名为c,存储point类型数据的队列
a.push(1); //在队列a的末尾添加int类型的元素1
b.push("abc"); //在队列b的末尾添加string类型的元素abc
point p;
p.x=10;
p.y=20;
c.push(p); //在队列c的末尾添加point类型的元素p,p.x=10,p.y=20
c.push({10,20}); //与c.push(p)等价
/*目前队列中的元素:
a: 1
b: "abc"
c: {10,20},{10,20};
*/
a.pop(); //将队列a的队头元素弹出,此时队列a为空
b.pop(); //将队列b的队头元素弹出,此时队列b为空
c.pop(); //将队列c的队头元素弹出,此时队列c还有一个元素{10,20}
return 0;
}5. 查看队列的长度
语法:.size()
eg:
#include <iostream>
#include <string>
#include <queue>
using namespace std;
struct point{ //声明point为struct类型
int x,y;
};
int main() {
queue<int> a; //定义一个名为a,存储int类型数据的队列
queue<string> b; //定义一个名为b,存储string类型数据的队列
queue<point> c; //定义一个名为c,存储point类型数据的队列
a.push(1); //在队列a的末尾添加int类型的元素1
b.push("abc"); //在队列b的末尾添加string类型的元素abc
b.push("cdef");
point p;
p.x=10;
p.y=20;
c.push(p); //在队列c的末尾添加point类型的元素p,p.x=10,p.y=20
c.push({10,20}); //与c.push(p)等价
while(c.size()){ //当队列c中存在元素时弹出队头
c.pop();
}
/*目前队列中的元素:
a: 1
b: "abc","cdef"
c:
*/
cout<<a.size()<<endl; //输出队列a的元素个数为1
cout<<b.size()<<endl; //输出队列b的元素个数为2
cout<<c.size()<<endl; //输出队列c的元素个数为0
return 0;
}6. 查看队列是否为空
语法:.empty()
eg:
#include <iostream>
#include <string>
#include <queue>
using namespace std;
struct point{ //声明point为struct类型
int x,y;
};
int main() {
queue<int> a; //定义一个名为a,存储int类型数据的队列
queue<string> b; //定义一个名为b,存储string类型数据的队列
queue<point> c; //定义一个名为c,存储point类型数据的队列
a.push(1); //在队列a的末尾添加int类型的元素1
b.push("abc"); //在队列b的末尾添加string类型的元素abc
b.push("cdef");
point p;
p.x=10;
p.y=20;
c.push(p); //在队列c的末尾添加point类型的元素p,p.x=10,p.y=20
c.push({10,20}); //与c.push(p)等价
while(!c.empty()){ //当队列c中存在元素时弹出队头
c.pop();
}
/*目前队列中的元素:
a: 1
b: "abc","cdef"
c:
*/
cout<<a.empty()<<endl; //队列a不空,输出0
cout<<b.empty()<<endl; //队列b不空,输出0
cout<<c.empty()<<endl; //队列c为空,输出1
return 0;
}2.2.2 BFS详解
1. 思想
- 当题目需要对一组数据进行扩展式搜索时可以考虑
BFS - 搜索时要将已经满足要求的点入队
- 不断地弹出队头,以队头元素进行扩展搜索,可以得到若干新的元素
- 对这些元素进行判断,满足继续搜索的条件则将该元素入队,否则具体问题具体分析,标记或抛弃。
- 一般来说,
BFS在第一次搜到答案时可以直接返回值,提前结束搜索
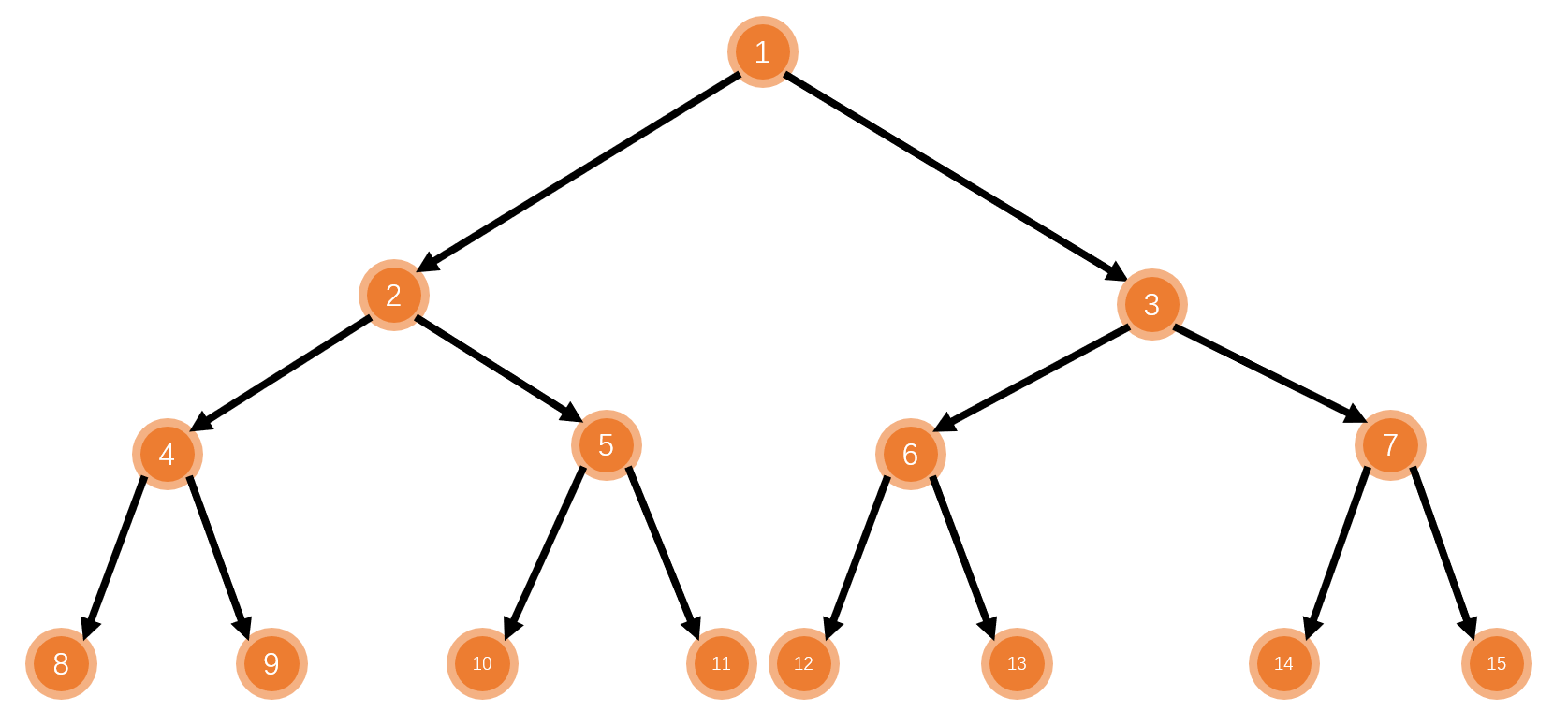
2. 走出迷宫(BFS)
描述
小明现在在玩一个游戏,游戏来到了教学关卡,迷宫是一个N*M的矩阵。
小明的起点在地图中用“S”来表示,终点用“E”来表示,障碍物用“#”来表示,空地用“.”来表示。
障碍物不能通过。小明如果现在在点(x,y)处,那么下一步只能走到相邻的四个格子中的某一个:(x+1,y),(x-1,y),(x,y+1),(x,y-1);
小明想要知道,现在他能否从起点走到终点。
输入格式:
本题包含多组数据。
每组数据先输入两个数字N,M
接下来N行,每行M个字符,表示地图的状态。
数据范围:
2<=N,M<=500
保证有一个起点S,同时保证有一个终点E.
输出格式:
每组数据输出一行,如果小明能够从起点走到终点,那么输出Yes,否则输出No
输入样例:
3 3
S..
..E
...
3 3
S##
###
##E输出样例
Yes
No分析
- 走出迷宫需要对每一个点进行搜索
- 首先需要记录
S的坐标 - 从
S开始搜索,需要偏移量数组 - 对于
BFS在搜随时,若搜到E点直接返回
BFS代码
#include <bits/stdc++.h>
using namespace std;
const int N=510;
int n,m;
char mp[N][N]; //存储地图
bool vis[N][N]; //标记是否走过该点
int s1,s2; //标记S的坐标
int dx[]={0,0,1,-1},dy[]={1,-1,0,0}; //初始化偏移量数组
struct point{ //用于记录点的信息
int x,y;
};
bool bfs(){
queue<point> st; //定义队列
st.push({s1,s2}); //将S点的信息入队
vis[s1][s2]=1; //标记S点为走过
while(!st.empty()){ //当队列不空时
auto p=st.front(); //使p获得队头的信息
st.pop(); //将队头出队
for(int i=0;i<4;i++){ //循环遍历偏移量数组,搜索四个方向
int l=p.x+dx[i],r=p.y+dy[i];
if(l>=1&&l<=n&&r>=1&&r<=m&&!vis[l][r]&&mp[l][r]!='#'){ //判断该点是否满足搜索条件
if(mp[l][r]=='E') return 1; //搜到答案直接返回
vis[l][r]=1; //标记该点已经走过
st.push({l,r}); //将该点入队,后续继续扩展该点搜索
}
}
}
return 0;
}
int main(){
while(cin>>n>>m){
//初始化清空数据
memset(vis,0,sizeof vis);
memset(mp,0,sizeof mp);
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>mp[i][j];
if(mp[i][j]=='S'){ //标记S的坐标
s1=i;
s2=j;
}
}
}
if(bfs()) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
return 0;
}3. 走迷宫
描述
给定一个 n×m 的二维整数数组,用来表示一个迷宫,数组中只包含 0 或 1,其中 0 表示可以走的路,1 表示不可通过的墙壁。
最初,有一个人位于左上角 (1,1) 处,已知该人每次可以向上、下、左、右任意一个方向移动一个位置。
请问,该人从左上角移动至右下角 (n,m) 处,至少需要移动多少次。
数据保证 (1,1) 处和 (n,m) 处的数字为 0,且一定至少存在一条通路。
输入格式
第一行包含两个整数 n 和 m。
接下来 n 行,每行包含 m 个整数(0 或 1),表示完整的二维数组迷宫。
输出格式
输出一个整数,表示从左上角移动至右下角的最少移动次数。
数据范围
1≤n,m≤100
输入样例:
5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0输出样例:
8代码
#include <bits/stdc++.h>
using namespace std;
const int N=110;
int mp[N][N]; //记录地图
bool vis[N][N]; //标记该点是否走过
int ans[N][N]; //存储答案
int n,m;
struct point{ //初始化point为struct类型
int x,y;
};
int dx[]={0,0,1,-1},dy[]={1,-1,0,0};
int bfs(){
queue<point> st; //定义队列
st.push({1,1}); //将起始点的信息入队
vis[1][1]=1; //标记起始点已经走过
while(!st.empty()){
auto p=st.front(); //使p获得队头的信息
st.pop(); //将队头出队
for(int i=0;i<4;i++){ //循环遍历偏移量数组,搜索四个方向
int l=p.x+dx[i],r=p.y+dy[i];
if(l>=1&&l<=n&&r>=1&&r<=m&&mp[l][r]==0&&!vis[l][r]){ //判断该点是否满足搜索条件
ans[l][r]=ans[p.x][p.y]+1; //更新答案
if(l==n&&r==m) return ans[n][m]; //搜到答案直接返回
vis[l][r]=1; //标记该点已经走过
st.push({l,r}); //将该点入队,后续继续扩展该点搜索
}
}
}
return ans[n][m]; //没有提前搜到答案,最后返回答案
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>mp[i][j];
}
}
cout<<bfs()<<endl;
return 0;
}2.3 DFS (深度优先搜索)
2.3.1 栈与递归
1. 栈的特点
- 栈是一种先进后出的数据结构
- 只允许对栈顶元素操作,不允许遍历
2. 简单递归
- 在计算机编程教材中都会提到递归的概念和应用,一般会用数学中的递推方程来讲递归的概念
- 在计算机系统中,递归是通过嵌套来实现的,涉及指针、地址、栈的使用。
- 从算法思想上看,递归是把大问题逐步缩小,直到变成最小的同类问题的过程
- 在递归的过程中,一个递归函数直接调用自己,将数据暂存于栈中是入栈过程,满足条件时返回是出栈过程
例题1 计算n的阶乘
eg:
#include <bits/stdc++.h>
using namespace std;
int n;
int fx(int u){
//cout<<"u = "<<u<<endl; //输出每一次递归调用后u的值
if(u==1){
return 1;
}
return fx(u-1)*u;
}
int main(){
cin>>n;
cout<<fx(n)<<endl;
return 0;
}例题2 走方格
描述
给定一个 n×m 的方格阵,沿着方格的边线走,从左上角 (0,0) 开始,每次只能往右或者往下走一个单位距离,问走到右下角 (n,m) 一共有多少种不同的走法。
输入
共一行,包含两个整数 n 和 m。
数据范围
0≤n,m≤10
输出
共一行,包含一个整数,表示走法数量。
样例输入
2 3样例输出
10分析
- 每次前进,都有两种方式可选
- 利用递归,产生不同的分支实现两种选择
- 当任意一个分支走到了终点,则为一种走法
代码
#include <bits/stdc++.h>
using namespace std;
int n,m;
int ans;
void step(int x,int y){
if(x==n&&y==m) ans++;
//当走下一步,没有超出终点时,利用递归进行选择的实现
if(x+1<=n) step(x+1,y);
if(y+1<=m) step(x,y+1);
}
int main(){
cin>>n>>m;
if(n!=0&&m!=0) step(0,0); //注意如果起始点和终点重合,则不需要走
cout<<ans<<endl;
return 0;
}
2.3.2 DFS详解
1. 思想
-
利用递归,将大问题拆分为同类型的小问题解决
-
一般情况下,从初识状态出发,进行扩展得到若干新的状态
-
选定一个状态继续深入,直到不再出现新的状态为止,然后回退,并将上一层的状态恢复
-
重复上述过程,直到将所有可以达到的状态全部遍历
-
一般来说,使用
DFS在提前搜索到答案时一般只进行标记,不提前返回或退出 -
当搜索过程中出现明显不满足目标的状态时可以提前返回,减少搜索次数
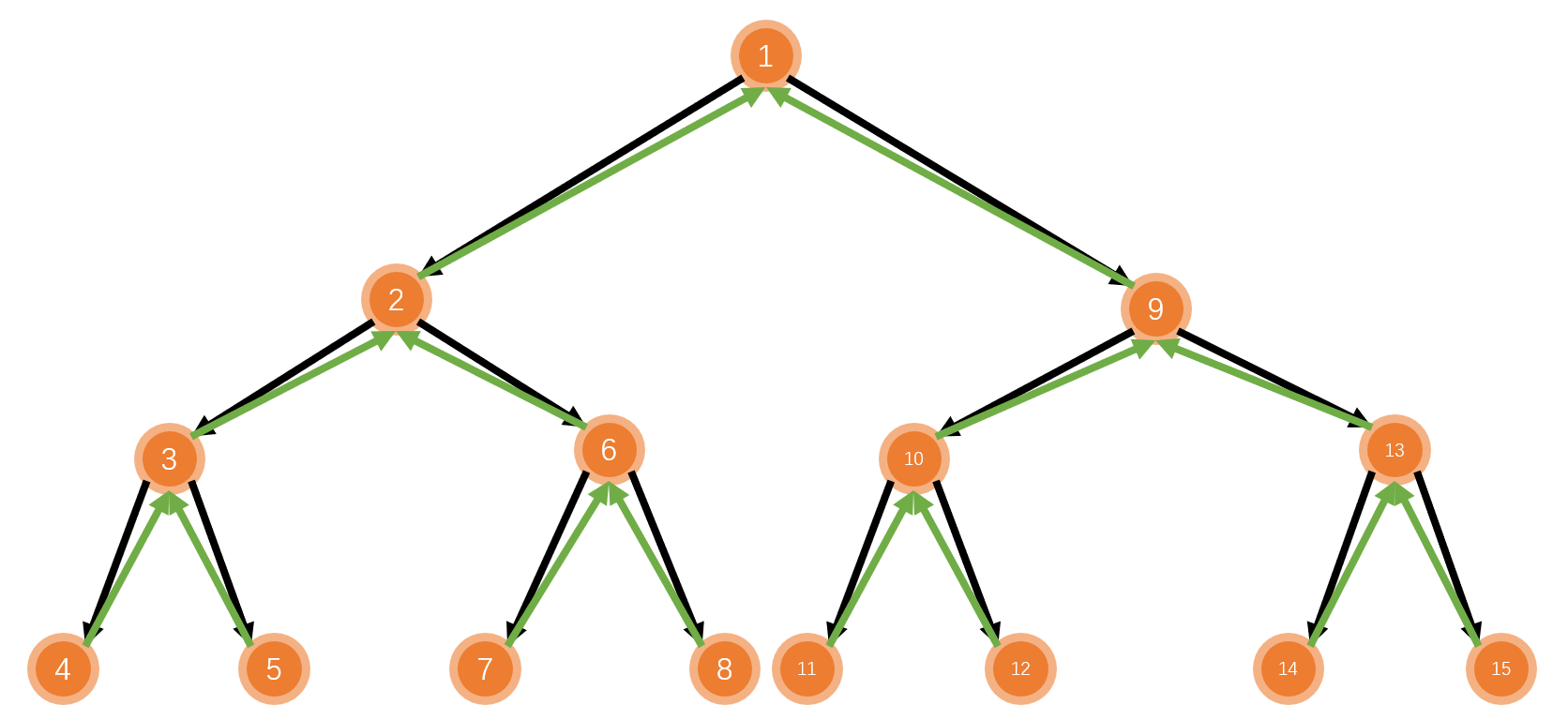
2. 走出迷宫(DFS)
描述
小明现在在玩一个游戏,游戏来到了教学关卡,迷宫是一个N*M的矩阵。
小明的起点在地图中用“S”来表示,终点用“E”来表示,障碍物用“#”来表示,空地用“.”来表示。
障碍物不能通过。小明如果现在在点(x,y)处,那么下一步只能走到相邻的四个格子中的某一个:(x+1,y),(x-1,y),(x,y+1),(x,y-1);
小明想要知道,现在他能否从起点走到终点。
输入格式:
本题包含多组数据。
每组数据先输入两个数字N,M
接下来N行,每行M个字符,表示地图的状态。
数据范围:
2<=N,M<=500
保证有一个起点S,同时保证有一个终点E.
输出格式:
每组数据输出一行,如果小明能够从起点走到终点,那么输出Yes,否则输出No
输入样例:
3 3
S..
..E
...
3 3
S##
###
##E输出样例
Yes
No分析
- 走出迷宫需要对每一个点进行搜索
- 首先需要记录
S的坐标 - 从
S开始搜索,需要偏移量数组 - 对于
DFS在搜索时,若搜到E点则标记答案
DFS代码
#include <bits/stdc++.h>
using namespace std;
const int N=510;
int n,m;
char mp[N][N]; //存储地图
bool vis[N][N]; //标记是否走过该点
int s1,s2; //标记S的坐标
int dx[]={0,0,1,-1},dy[]={1,-1,0,0}; //初始化偏移量数组
bool flag; //标记是否可以走到E
void dfs(int x,int y){
if(mp[x][y]=='E'){
flag=1; //标记答案
}
for(int i=0;i<4;i++){ //循环遍历偏移量数组,搜索四个方向
int l=x+dx[i],r=y+dy[i];
if(l>=1&&l<=n&&r>=1&&r<=m&&!vis[l][r]&&mp[l][r]!='#'){ //判断该点是否满足搜索条件
vis[l][r]=1; //标记该点已经走过
dfs(l,r); //继续以该点搜索
}
}
}
int main(){
while(cin>>n>>m){ //多实例输入
//初始化清空数据
flag=0;
memset(vis,0,sizeof vis);
memset(mp,0,sizeof mp);
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>mp[i][j];
if(mp[i][j]=='S'){ //标记S的坐标
s1=i;
s2=j;
}
}
}
dfs(s1,s2);
if(flag) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
return 0;
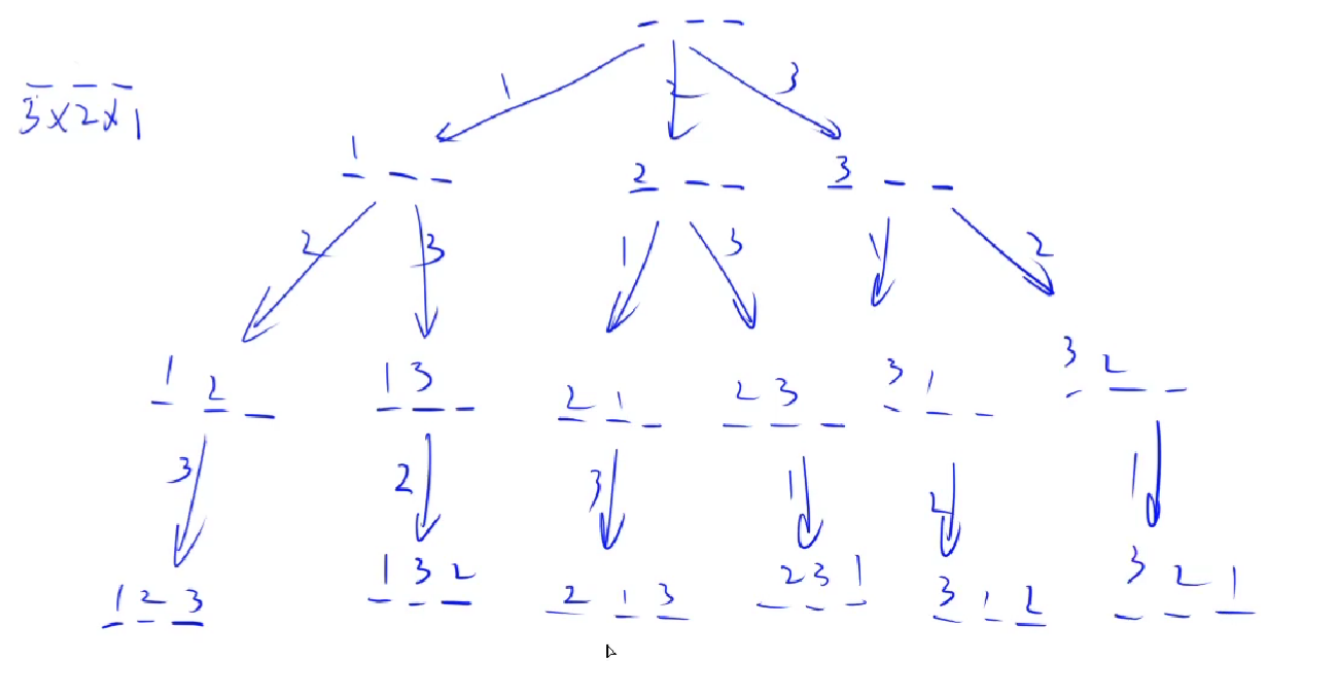
}3. 排列数字
描述
给定一个整数 n,将数字 1∼n 排成一排,将会有很多种排列方法。
现在,请你按照字典序将所有的排列方法输出。
输入格式
共一行,包含一个整数 n。
输出格式
按字典序输出所有排列方案,每个方案占一行。
数据范围
1≤n≤9输入样例:
3输出样例:
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
分析:
-
对于全排列,我们需要明确排列的顺序,按照字典序排列分析
-
递归处理,每一次递归视为一次选择,递归的层数即为选择数
-
对于每一次的选择进行标记,记录选择并递归到下一层
-
回退时要对上一次的标记的状态进行还原
-
代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+3;
int ans[N];
int a[N];
bool vis[N]; //标记是否使用过该数
int n;
void dfs(int u){
if(u==n){
for(int i=0;i<n;i++){
cout<<ans[i]<<" ";
}
cout<<endl;
return ;
}
for(int i=0;i<n;i++){
if(!vis[a[i]]){
vis[a[i]]=1; //标记为使用过
ans[u]=a[i]; //选择该数
dfs(u+1); //递归到下一层
vis[a[i]]=0; //恢复状态
}
}
}
int main(){
cin>>n;
for(int i=0;i<n;i++){ //初始化
a[i]=i+1;
}
dfs(0);
return 0;
}扩展:
- 利用
STL中的next_permutation函数
next_permutation按照字典序生成下一个排列组合
复杂度O(n)
排列范围[first,last)
代码:
#include <bits/stdc++.h>
using namespace std;
int main(){
int n,a[1000]; //a[]用于存放排列
cin>>n;
for(int i=1;i<=n;i++){
a[i]=i; //初始化排列
}
do{
for(int i=1;i<=n;i++){ //循环输出排列
cout<<a[i]<<" ";
}
cout<<endl;
}while(next_permutation(a+1,a+n+1)); //如果下一个排列存在,则生成排列并执行
return 0;
}4. N皇后
描述
给出一个 nn×n的国际象棋棋盘,你需要在棋盘中摆放nn个皇后,使得任意两个皇后之间不能互相攻击。具体来说,不能存在两个皇后位于同一行、同一列,或者同一对角线。请问共有多少种摆放方式满足条件。
输入描述:
一行,一个整数n(1≤n≤12),表示棋盘的大小。
输出描述:
输出一行一个整数,表示总共有多少种摆放皇后的方案,使得它们两两不能互相攻击。
样例输入
4样例输出
2分析
- 由于皇后不能互相攻击到,故棋盘的每一行,每一列及其有皇后存在的对角线的平行线上有且只有一个皇后
- 递归处理,每一次递视为一次对棋子的判断,递归的层数视为棋盘的层数,每一层选择放置一个皇后
- 对于递归的每一层,遍历这层棋盘的格子,判断以该格子的列和对角线的平行线上是否存在过皇后
- 若放置皇后,则需要对放置的格子所在的列和对角线的平行线进行标记
- 递归处理上述过程,直到将皇后放置完毕
- 对于对角线的处理,我们 可以利用数学关系,转换为截距进行标记
k = i + u或k = i - u
代码
#include <bits/stdc++.h>
using namespace std;
const int N=510;
bool y[N],l[N],r[N]; //标记是否存在皇后
int n;
int ans;
void dfs(int u){
if(u==n){
ans++;
return ;
}
for(int i=0;i<n;i++){
if(!y[i]&&!l[u+i+n]&&!r[u-i+n]){ //若该格子的列和对角线的平行线上没有存在过皇后
y[i]=l[u+i+n]=r[u-i+n]=1; //标记
dfs(u+1); //递归到下一层
y[i]=l[u+i+n]=r[u-i+n]=0; //恢复现场
}
}
}
int main(){
cin>>n;
dfs(0);
cout<<ans<<endl;
}
评论
Deprecated: preg_replace(): Passing null to parameter #3 ($subject) of type array|string is deprecated in /var/www/html/wp-content/themes/argon/functions.php on line 1748