2. 基础数据结构初识

本文最后更新于 963 天前，其中的信息可能已经有所发展或是发生改变。

2.1 链表

2.1.1 单链表

概念：

链表是一种物理存储单元上非连续的存储结构，数据元素的逻辑顺序是通过链表中的指针链接实现的
链表由一系列结点组成，每个结点中分为存储数据元素的数据域和存储下一个结点的指针域

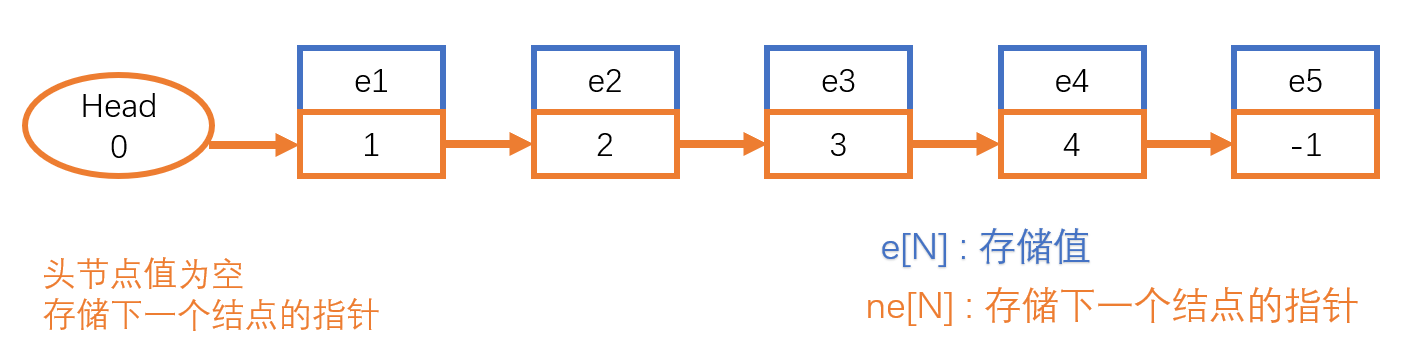
操作思想

插入：新建一个结点，改变前一个结点的指针指向新建的结点

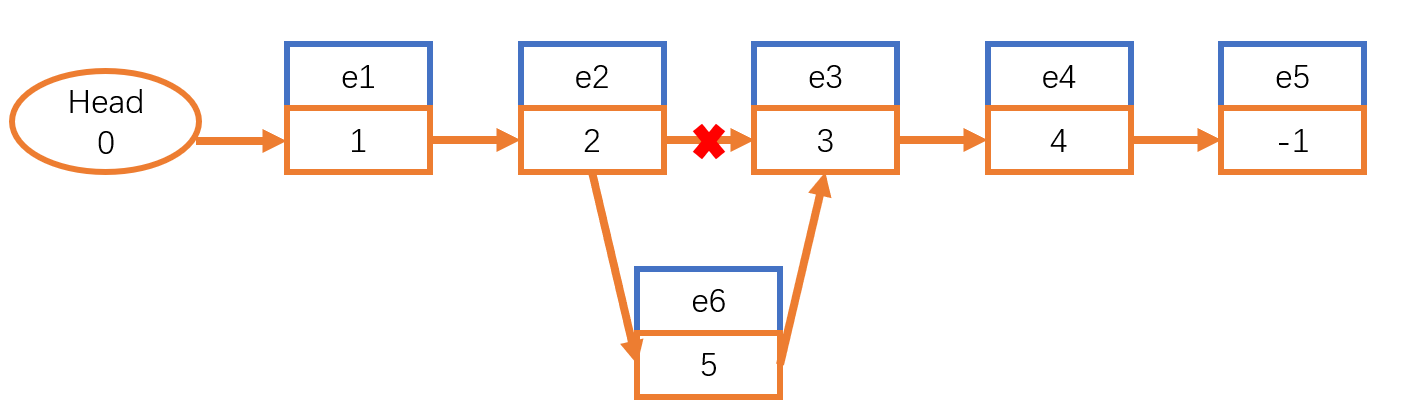
删除：将删除结点的前一个结点的指针指向该节点的后一个结点的指针

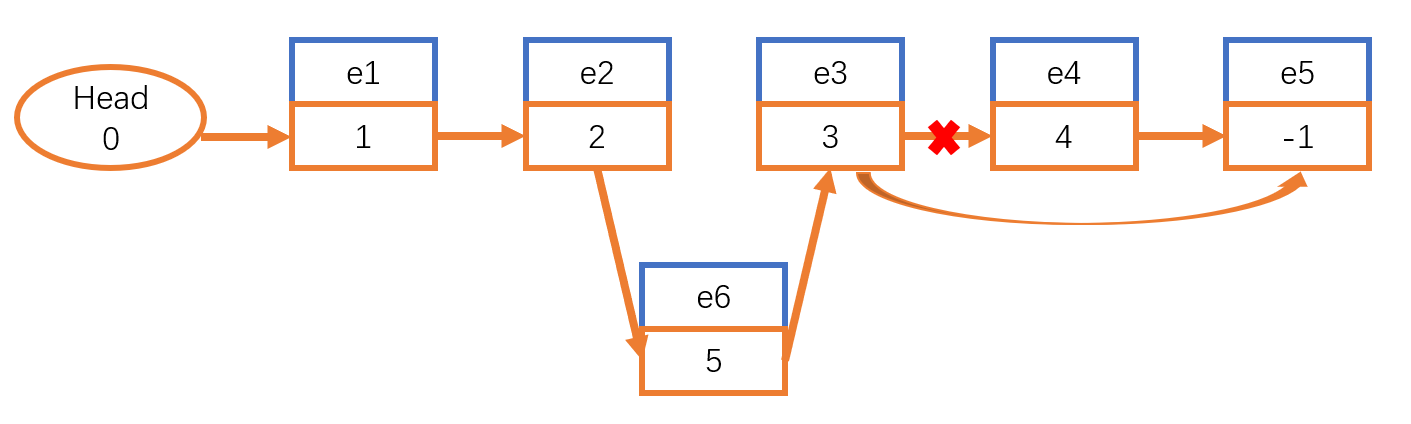
模板

 /*  可使用数组、结构体等模拟链表，malloc和new模拟动态链表较慢，而结构体模拟代码繁琐，故采用静态数组模拟链表  */
 
const int N=1e6+10;  //根据需要开辟链表大小
 
int e[N],ne[N],head=-1,idx=0;  //e[N]存储值，ne[N]存储下一个结点，初始化head头结点，idx充当指针作用
 
void head_add(int x){  //在头部插入x
    e[idx]=x;
    ne[idx]=head;
    head=idx++;
}
 
void add(int k,int x){  //在下标k后面插入x
    e[idx]=x;
    ne[idx]=ne[k];
    ne[k]=idx++;
}
 
void remove(int k){  //删除下标k后面的结点
    ne[k]=ne[ne[k]];
}

例题 826.单链表

原题链接

描述

实现一个单链表，链表初始为空，支持三种操作：

1.向链表头插入一个数；
2.删除第 k 个插入的数后面的数；
3.在第 k 个插入的数后插入一个数。

现在要对该链表进行 M 次操作，进行完所有操作后，从头到尾输出整个链表。

注意:题目中第 k 个插入的数并不是指当前链表的第 k 个数。例如操作过程中一共插入了 n 个数，则按照插入的时间顺序，这 n 个数依次为：第 1 个插入的数，第 2 个插入的数，…第 n 个插入的数。

输入格式
第一行包含整数 M，表示操作次数。

接下来 M 行，每行包含一个操作命令，操作命令可能为以下几种：

H x，表示向链表头插入一个数 x。
D k，表示删除第 k 个插入的数后面的数（当 k 为 0 时，表示删除头结点）。
I k x，表示在第 k 个插入的数后面插入一个数 x（此操作中 k 均大于 0）。

输出格式
共一行，将整个链表从头到尾输出。

数据范围
1≤M≤100000
所有操作保证合法。

输入样例：

输出样例：

 6 4 6 5

代码

 #include <bits/stdc++.h>
using namespace std;
 
const int N=1e6+10;
 
int e[N],ne[N],head=-1,idx=0; 
 
void head_add(int x){  //在头部插入x
    e[idx]=x;
    ne[idx]=head;
    head=idx++;
}
 
void add(int k,int x){  //在下标k后面插入x
    e[idx]=x;
    ne[idx]=ne[k];
    ne[k]=idx++;
}
 
void remove(int k){  //删除下标为k的结点
    ne[k]=ne[ne[k]];
}
 
int main(){
    int m;
    cin>>m;  //读入操作次数
 
    while(m--){
        string s;
        cin>>s;  //读入操作
 
        if(s=="H"){  //头部插入
            int x;
            cin>>x;
            head_add(x);
        }
        else if(s=="D"){  //删除操作
            int k;
            cin>>k; 
            if(k==0){
                head=ne[head];
            }
            else{
                remove(k-1);  //idx从0开始，下标为k-1
            }
        }
        else if(s=="I"){  //插入操作
            int k,x;
            cin>>k>>x;
            add(k-1,x);
        }
    }
 
    for(int i=head;i!=-1;i=ne[i]){  //遍历输出
        cout<<e[i]<<" ";
    }
 
    return 0;
 
}

2.1.2 双链表

概念：

在单链表的基础上，取消头结点，换为左端点和右端点，每个结点的指针域存储其左边结点的指针和右边结点的指针

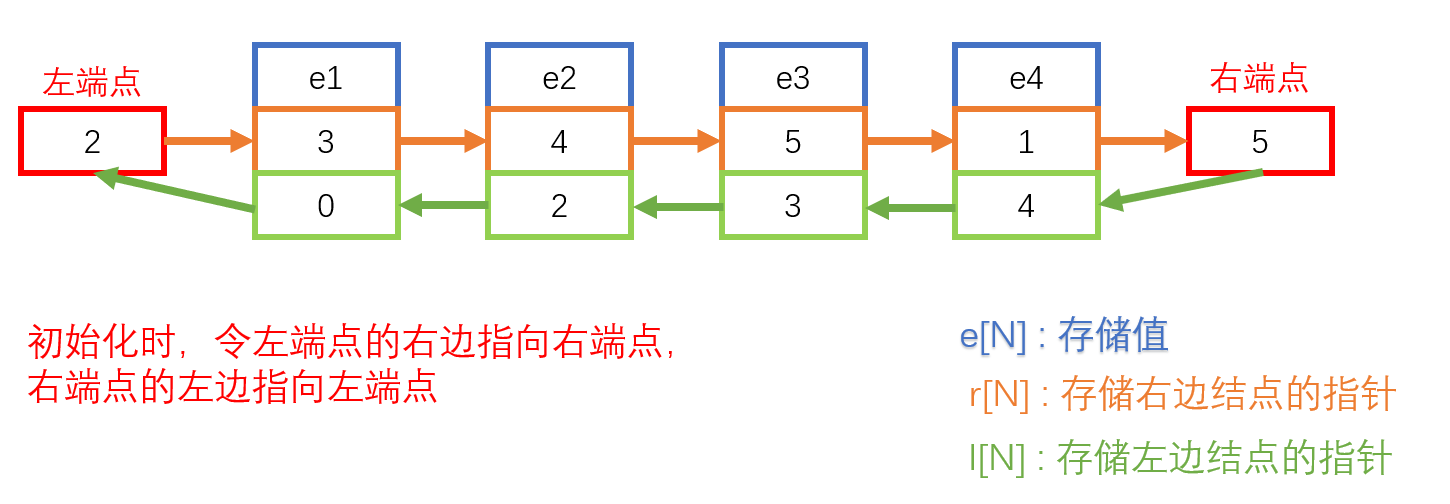
操作思想

插入：思想同单链表，新建结点后，依次更改左右结点的左右指针的指向
删除：思想同单链表，将删除结点的左右结点的左右指针改向，跳过该节点

模板

 const int N=1e6+10;  //根据需要开辟链表大小
 
int e[N],r[N],l[N],idx;  //e[N]存储值，r[N]存储右结点，l[N]存储左结点，idx用于计数
 
void init(){  //初始化链表
    r[0]=1;  //初始化左端点右边为右端点
    l[1]=0;  //初始化右端点左边为左端点
    idx=2;  //已经用掉了左端点和右端点，下标从2开始
}
 
void add(int k,int x){  //在下标k右边插入x
    e[idx]=x;  //存储新结点的值
    l[idx]=k;  //新结点的左边指针为k
    r[idx]=r[k];  //新结点的右边指针为左结点的右指针r[k]
    l[r[k]]=idx;  //修改新结点右边结点的左指针为新结点下标idx
    r[k]=idx++;  //修改新结点左边结点的右指针为新结点下标idx
}
 
//调用时，若在第k个数的右边插入x则为 add(k+1,x) idx从2开始，故为k+1
//调用时，若在第k个数的左边插入x则为 add(l[k+1],x) 相当于在k左边的点的右边插入x
 
void remove(int k){  //删除下标为k的点
    r[l[k]]=r[k];
    l[r[k]]=l[k];
}

例题 827. 双链表

原题链接

描述

实现一个双链表，双链表初始为空，支持 5 种操作：

1.在最左侧插入一个数；
2.在最右侧插入一个数；
3.将第 k 个插入的数删除；
4.在第 k 个插入的数左侧插入一个数；
5.在第 k 个插入的数右侧插入一个数

现在要对该链表进行 M 次操作，进行完所有操作后，从左到右输出整个链表。

输入格式
第一行包含整数 M，表示操作次数。

接下来 M 行，每行包含一个操作命令，操作命令可能为以下几种：

1.L x，表示在链表的最左端插入数 x。
2.R x，表示在链表的最右端插入数 x。
3.D k，表示将第 k 个插入的数删除。
4.IL k x，表示在第 k 个插入的数左侧插入一个数。
5.IR k x，表示在第 k 个插入的数右侧插入一个数。

输出格式
共一行，将整个链表从左到右输出。

数据范围
1≤M≤100000
所有操作保证合法。

输入样例：

 10
R 7
D 1
L 3
IL 2 10
D 3
IL 2 7
L 8
R 9
IL 4 7
IR 2 2

输出样例：

 8 7 7 3 2 9

代码

 #include <bits/stdc++.h>
using namespace std;
 
const int N=1e6+10;
 
int e[N],r[N],l[N],idx=2;
 
void add(int k,int x){
    e[idx]=x;
    l[idx]=k;
    r[idx]=r[k];
    l[r[k]]=idx;
    r[k]=idx++;
}
 
void remove(int k){
    r[l[k]]=r[k];
    l[r[k]]=l[k];
}
 
int main()
{
 
    r[0]=1,l[1]=0;  //初始化链表
 
    int m;
    cin>>m;  //读入操作次数
 
    while(m--){
        string s;
        cin>>s;  //读入操作
 
        if(s=="L"){  //最左端插入x
            int x;
            cin>>x;
            add(0,x);  //最左端的端点下标为0
        }
        else if(s=="R"){  //最右端插入x
            int x;
            cin>>x;
            add(l[1],x);  //最右端的端点下标为下标为1的左边，即l[1]
        }
        else if(s=="D"){  //删除操作
            int k;
            cin>>k;
            remove(k+1);  //idx从2开始，下标为k+1
        }
        else if(s=="IL"){  //在第k个数左边插入x
            int k,x;
            cin>>k>>x;
            add(l[k+1],x);  //即在第k个数左边的数的右边插入x
        }
        else if(s=="IR"){  //在第k个数右边插入x
            int k,x;
            cin>>k>>x;
            add(k+1,x);
        }
    }
 
    for(int i=r[0];i!=1;i=r[i]){  //遍历输出
        cout<<e[i]<<" ";
    }
 
    return 0;
 
}

2.2 栈

2.1.1 模拟栈

概念：

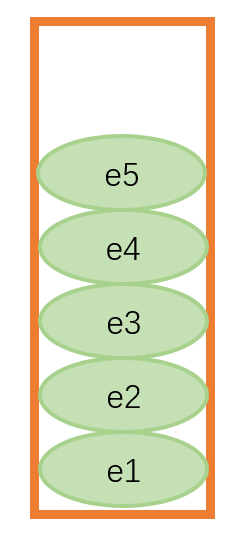
栈是一种先进后出的数据结构
只允许对栈顶元素操作，不允许遍历

操作思想

利用静态数组模拟栈
实现进栈，出栈等操作

模板

 const int N=1e6+10;  
 
int stk[N],tt=0;  //stk[N]用于模拟栈，类型可自定义，tt表示栈顶
 
void add(int x){  //栈顶插入x
    stk[++tt]=x;
}
 
int top(){  //返回栈顶元素
    return stk[tt];
}
 
void pop(){  //弹出栈顶元素
    tt--;
}
 
bool empty(){  //判断是否为空
    return tt==0;  //若为空则返回true
}

例题 828.模拟栈

原题链接

描述

实现一个栈，栈初始为空，支持四种操作：

push x – 向栈顶插入一个数 x；
pop – 从栈顶弹出一个数；
empty – 判断栈是否为空；
query – 查询栈顶元素。

现在要对栈进行 M 个操作，其中的每个操作 3 和操作 4 都要输出相应的结果。

输入格式
第一行包含整数 M，表示操作次数。

接下来 M 行，每行包含一个操作命令，操作命令为 push x，pop，empty，query 中的一种。

输出格式
对于每个 empty 和 query 操作都要输出一个查询结果，每个结果占一行。

其中，empty 操作的查询结果为 YES 或 NO，query 操作的查询结果为一个整数，表示栈顶元素的值。

数据范围
1≤M≤100000,
1≤x≤109
所有操作保证合法。

输入样例：

 10
push 5
query
push 6
pop
query
pop
empty
push 4
query
empty

输出样例：

 5
5
YES
4
NO

代码

 #include <bits/stdc++.h>
using namespace std;
 
const int N=1e6+10;
 
int stk[N],tt=0;
 
void add(int x){
    stk[++tt]=x;
}
 
void pop(){
    tt--;
}
 
bool empty(){  //判断是否为空
    return tt==0;  //若为空则返回true
}
 
int top(){
    return stk[tt];
}
 
int main()
{
    int n;
    cin>>n;
 
    while(n--){
        string s;
        cin>>s;
        if(s=="push"){
            int x;
            cin>>x;
            add(x);
        }
        else if(s=="pop"){
            pop();
        }
        else if(s=="empty"){
            if(empty()){
                cout<<"YES"<<endl;
            }
            else cout<<"NO"<<endl;
        }
        else if(s=="query"){
            cout<<top()<<endl;
        }
    }
 
    return 0;
 
}

2.1.2 单调栈

概念

栈中的元素满足某种单调性质

应用

常见模型：找出每个数左边离它最近的比它大/小的数

例题 830. 单调栈

原题链接

描述

给定一个长度为 N 的整数数列，输出每个数左边第一个比它小的数，如果不存在则输出 −1。

输入格式
第一行包含整数 N，表示数列长度。

第二行包含 N 个整数，表示整数数列。

输出格式
共一行，包含 N 个整数，其中第 i 个数表示第 i 个数的左边第一个比它小的数，如果不存在则输出 −1。

数据范围
1≤N≤105
1≤数列中元素≤109
输入样例：

 5
3 4 2 7 5

输出样例：

 -1 3 -1 2 2

代码

 #include <bits/stdc++.h>
using namespace std;
 
const int N=1e6+10;
 
int stk[N],tt=0;
 
int main(){
    int n;
    cin>>n;
    while(n--){
        int x;
        cin>>x;
        while(tt>0&&x<=stk[tt]) tt--;  //当栈不为空时，判断x与栈顶元素关系，若构成逆序，则删除栈顶元素
        if(tt>0) cout<<stk[tt]<<" ";
        else cout<<-1<<" ";
        stk[++tt]=x;
    }
 
    return 0;
 
}

2.3 队列

2.3.1 模拟队列

概念

是一种先进先出的数据结构，它有两个出口
队列容器允许从尾端新增元素，从头端移除元素
队列中只有队头和队尾才可以被外界使用，故队列不允许遍历

操作思想

利用静态数组模拟队列
实现入队，出队等操作

模板

 const int N=1e6+10;
 
int que[N],hh=0,tt=-1;  //que[N]用于模拟队列，类型可自定义，hh为队头，tt为队尾
 
void add(int x){  //队尾插入x
    que[++tt];
}
 
int top(){  //返回队头元素
    return que[hh];
}
 
int back(){  //返回队尾元素
    return que[tt];
}
 
void pop(){  //弹出队头元素
    hh++;
}
 
bool empty(){  //判断是否为空
    return tt<hh;  //若为空则返回true
}

例题 829. 模拟队列

原题链接

描述

实现一个队列，队列初始为空，支持四种操作：

push x – 向队尾插入一个数 x；
pop – 从队头弹出一个数；
empty – 判断队列是否为空；
query – 查询队头元素。

现在要对队列进行 M 个操作，其中的每个操作 3 和操作 4 都要输出相应的结果。

输入格式
第一行包含整数 M，表示操作次数。

接下来 M 行，每行包含一个操作命令，操作命令为 push x，pop，empty，query 中的一种。

输出格式
对于每个 empty 和 query 操作都要输出一个查询结果，每个结果占一行。

其中，empty 操作的查询结果为 YES 或 NO，query 操作的查询结果为一个整数，表示队头元素的值。

数据范围
1≤M≤100000,
1≤x≤109,
所有操作保证合法。

输入样例：

 10
push 6
empty
query
pop
empty
push 3
push 4
pop
query
push 6

输出样例：

 NO
6
YES
4

代码

 #include <bits/stdc++.h>
using namespace std;
 
const int N=1e6+10;
 
int que[N],hh=0,tt=-1;
 
void add(int x){
    que[++tt]=x;
}
 
void pop(){
    hh++;
}
 
bool empty(){
    return tt<hh;
}
 
int top(){
    return que[hh];
}
 
int main()
{
    int m;
    cin>>m;
 
    while(m--){
        string s;
        cin>>s;
        if(s=="push"){
            int x;
            cin>>x;
            add(x);
        }
        else if(s=="pop"){
            pop();
        }
        else if(s=="empty"){
            if(empty()) cout<<"YES"<<endl;
             else cout<<"NO"<<endl;
        }
        else if(s=="query"){
            cout<<top()<<endl;
        }
    }
 
    return 0;
 
}

2.3.2 单调队列

概念

队列中的元素满足某种单调性质

应用

常见模型：找出滑动窗口中的最大值/最小值

例题 154. 滑动窗口

原题链接

描述

给定一个大小为 n≤106 的数组。

有一个大小为 k 的滑动窗口，它从数组的最左边移动到最右边。

你只能在窗口中看到 kk 个数字。

每次滑动窗口向右移动一个位置。

以下是一个例子：

该数组为 [1 3 -1 -3 5 3 6 7]，k 为 3。

窗口位置	最小值	最大值
[1 3 -1] -3 5 3 6 7	-1	3
1 [3 -1 -3] 5 3 6 7	-3	3
1 3 [-1 -3 5] 3 6 7	-3	5
1 3 -1 [-3 5 3] 6 7	-3	5
1 3 -1 -3 [5 3 6] 7	3	6
1 3 -1 -3 5 [3 6 7]	3	7

你的任务是确定滑动窗口位于每个位置时，窗口中的最大值和最小值。

输入格式

输入包含两行。

第一行包含两个整数 n 和 k，分别代表数组长度和滑动窗口的长度。

第二行有 n 个整数，代表数组的具体数值。

同行数据之间用空格隔开。

输出格式

输出包含两个。

第一行输出，从左至右，每个位置滑动窗口中的最小值。

第二行输出，从左至右，每个位置滑动窗口中的最大值。

输入样例：

 8 3
1 3 -1 -3 5 3 6 7

输出样例：

 -1 -3 -3 -3 3 3
3 3 5 5 6 7

代码

 #include <bits/stdc++.h>
using namespace std;
 
const int N=1e6+10;
 
int a[N],q[N],hh,tt;
 
int main()
{
    int n,m;
    cin>>n>>m;
 
    for(int i=0;i<n;i++) scanf("%d",&a[i]);  //读入数组元素
 
    hh=0,tt=-1;  //初始化窗口队列，该队列存储a的下标
    for(int i=0;i<n;i++) 
    {
        if(hh<=tt&&i-m+1>q[hh]) hh++;  //当i-m+1大于当前队头下标时，队头出队
 
        while(hh<=tt&&a[q[tt]]>=a[i]) tt--;  //当窗口内队尾下标对应的数值大于当前进入窗口的值且hh<=tt时，则队尾更新为前一个元素下标，维护队头为最小值
 
        q[++tt]=i;  //当前值入队
 
        if(i>=m-1) printf("%d ",a[q[hh]]);  //输出队头
    }
 
    cout<<endl;
 
    hh=0,tt=-1;  //再次初始化窗口队列，该队列存储a的下标
    for(int i=0;i<n;i++) 
    {
        if(hh<=tt&&i-m+1>q[hh]) hh++;  //当i-m+1大于当前队头下标时，队头出队
 
        while(hh<=tt&&a[q[tt]]<=a[i]) tt--;  //当窗口内队尾下标对应的数值小于当前进入窗口的值且hh<=tt时，则队尾更新为前一个元素下标，维护队头为最大值
 
        q[++tt]=i;  //当前值入队
 
        if(i>=m-1) printf("%d ",a[q[hh]]);  //输出队头
    }
 
    return 0;
 
}

2.4 堆

概念

本质为一颗完全二叉树
以小根堆为例，其每个结点的值，均小于等于左右子节点，即根节点为整棵树的最小值

操作思想

存储方式：用一维数组存储，设根节点的下标是i,则左儿子是2*i，右儿子是2*i+1

 //对无序的一维数组进行建堆(小根堆)
for(int i=n/2;i;i--) down(i);  //n表示数组大小，利用down操作对堆进行排序

排序：若某结点的值发生改变，则判断其与父节点和左右两个子结点的大小关系，再进行上移或下移，递归处理直至满足当前堆的性质。
以小根堆为例：若某一结点的值增大，则需要将其向下移动，直到不能下移为止。
删除和修改元素：将最后插入的元素覆盖掉需要修改的元素，之后从修改元素的位置重新对堆进行排序

2.4.1 堆排序

思想

将数据以堆的形式进行存储
仅实现堆的上移或下移操作对堆中的数据进行排序
不考虑对堆中的数据进行修改

模板

 ////以小根堆为例
 
const int N=1e6+10;  //堆的大小
 
int h[N];  //h[N]为堆 
 
int idx;   //idx表示当前的结点在数组中的下标
 
void down(int u){  //完成下移操作，u表示父节点
 
    int t=u;  //t用于比较
    int p=u*2;  //p表示左儿子节点的下标 p+1表示右儿子
 
    if(p<=idx&&h[p]<h[t]) t=p;   //在树的大小范围内，若左儿子小于父节点，则记录t
    if(p+1<=idx&&h[p+1]<h[t]) t=p+1;  //在树的大小范围内，若右儿子小于父节点，则记录t
    if(u!=t){  //若t与原来的u不相等，说明u需要下移
 
        swap(h[t],h[u]);
        down(t);  //递归处理，直到不能下移
 
    }
 
}
 
void up(int u){  //完成上移操作，u表示子结点
 
    int t=u>>1;   //t表示u的父结点的下标，t=u/2
 
    if(t&&h[u]<h[t]){  //当t>0并且子结点的值小于父结点的值，说明u要上移
 
        swap(h[u],h[t]);
        up(t);  //递归处理，直到不能上移
 
    }
 
}

例题 838. 堆排序

原题链接

描述

输入一个长度为 n 的整数数列，从小到大输出前 m 小的数。

输入格式
第一行包含整数 n 和 m。

第二行包含 n 个整数，表示整数数列。

输出格式
共一行，包含 m 个整数，表示整数数列中前 m 小的数。

数据范围
1≤m≤n≤105，
1≤数列中元素≤109

输出样例：

 5 3
4 5 1 3 2

输出样例：

 1 2 3

代码

 #include <bits/stdc++.h>
using namespace std;
 
const int N=1e6+10;
 
int h[N];
 
int idx;
 
void down(int u){
 
    int p=u*2;
 
    int t=u;
 
    if(p<=idx&&h[p]<h[t]) t=p;
    if(p+1<=idx&&h[p+1]<h[t]) t=p+1;
    if(u!=t){
 
        swap(h[t],h[u]);
        down(t);
 
    }
 
}
 
int main(){
 
    int n,m;
 
    cin>>n>>m;
 
    for(int i=0;i<n;i++) cin>>h[++idx];  //建堆的操作
 
    for(int i=n/2;i;i--) down(i);
 
    while(m--){
 
        cout<<h[1]<<" ";  //将堆顶元素输出
        h[1]=h[idx--];  //将堆最后的值覆盖堆顶的值，idx--使得删除堆最后的元素
        down(1);  //将堆顶的元素执行下移操作，进行排序
 
    }
 
    return 0;
 
}

2.4.2 可操作的堆

支持的操作

插入一个数
求集合中的最小值
删除最小值
删除任意一个元素
修改任意一个元素

模板(注释解析版)

 //以小根堆为例
 
const int N=1e6+10;  //堆的大小
 
int idx,m;  //idx表示当前的结点在数组中的下标，m表示插入的第m个数
 
int h[N],ph[N],hp[N];
    //h[N]为堆 
    //ph[N]存储 第m个数 在h[N]中的下标  为idx 即ph[m]=idx
    //hp[N]存储 在h[N]中 下标为idx的数 为插入第m个数 即hp[idx]=m
    //由于我们在涉及到操作第m个元素时需要知道该元素是插入的第m个数，故需要p[h]和hp[N]的映射关系来确定
 
void h_swap(int a,int b){  //完成交换操作
 
    swap(ph[hp[a]],ph[hp[b]]);
    //通过hp[a]找到idx=a是插入的第m_i个数 ph[hp[a]]就可以得到其在h[N]中的下标
    //通过hp[b]找到idx=a是插入的第m_j个数 ph[hp[b]]就可以得到其在h[N]中的下标
    //交换idx的映射关系
 
    swap(hp[a],hp[b]);
    //交换m的映射关系
 
    swap(h[a],h[b]);
    //交换值
}
 
void down(int u){  //完成下移操作
    //u表示父结点
 
    int t=u;  //t用于比较
    int p=u*2;  //p表示左儿子节点的下标 p+1表示右儿子
 
    if(p<=idx&&h[p]<h[t]) t=p;  
    //p表示左儿子的下标，要在树的大小范围内，若左儿子小于父节点，则暂时记录t，最后与父节点u交换
 
    if(p+1<=idx&&h[p+1]<h[t]) t=p+1;
    //p+1表示右儿子的下标，要在树的大小范围内，若右儿子小于父节点，则暂时记录t，最后与父节点u交换
 
    if(t!=u){  //若t与原来的u不相等，说明u需要下移
        h_swap(t,u);  //交换
        down(t);  //递归处理，直到不能下移
    }
 
}
 
void up(int u){  //完成上移操作
    //u表示子结点
 
    int t=u>>1;  //t表示u的父结点的下标
 
    if(t&&h[u]<h[t]){  //当t>0并且子结点的值小于父结点的值，说明u要上移
        h_swap(t,u);  //交换
        up(t);  //递归处理，直到不能上移
    }
 
}

模板(简注释)

 //以小根堆为例
 
const int N=1e6+10;  //堆的大小
 
int idx,m;  //idx表示当前的结点在数组中的下标，m表示插入的第m个数
 
int h[N],ph[N],hp[N];
 
void h_swap(int a,int b){
    swap(ph[hp[a]],ph[hp[b]]);  //交换idx的映射关系
    swap(hp[a],hp[b]);  //交换m的映射关系
    swap(h[a],h[b]);  //交换值
}
 
void down(int u){
    int t=u;
    int p=u*2;  //p表示左儿子节点的下标 p+1表示右儿子
    if(p<=idx&&h[p]<h[t]) t=p;
    if(p+1<=idx&&h[p+1]<h[t]) t=p+1;
    if(t!=u){
        h_swap(t,u);
        down(t);  //递归处理，直到不能下移
    }
}
 
void up(int u){
    int t=u>>1;
    if(t&&h[u]<h[t]){
        h_swap(t,u);
        up(t);  //递归处理，直到不能上移
    }
}

例题 839. 模拟堆

原题链接

描述

维护一个集合，初始时集合为空，支持如下几种操作：

I x，插入一个数 x；
PM，输出当前集合中的最小值；
DM，删除当前集合中的最小值（数据保证此时的最小值唯一）；
D k，删除第 k 个插入的数；
C k x，修改第 k 个插入的数，将其变为 x；
现在要进行 N 次操作，对于所有第 2 个操作，输出当前集合的最小值。

输入格式
第一行包含整数 N。

接下来 N 行，每行包含一个操作指令，操作指令为 I x，PM，DM，D k 或 C k x 中的一种。

输出格式
对于每个输出指令 PM，输出一个结果，表示当前集合中的最小值。

每个结果占一行。

数据范围
1≤N≤105
−109≤x≤109
数据保证合法。

输入样例：

 8
I -10
PM
I -10
D 1
C 2 8
I 6
PM
DM

输出样例：

 -10
6

代码

 #include <bits/stdc++.h>
using namespace std;
 
const int N=1e6+10;  //堆的大小
 
int idx,m;  //idx表示当前的结点在数组中的下标，m表示插入的第m个数
 
int h[N],ph[N],hp[N];
 
void h_swap(int a,int b){
    swap(ph[hp[a]],ph[hp[b]]);  //交换idx的映射关系
    swap(hp[a],hp[b]);  //交换m的映射关系
    swap(h[a],h[b]);  //交换值
}
 
void down(int u){
    int t=u;
    int p=u*2;  //p表示左儿子节点的下标 p+1表示右儿子
    if(p<=idx&&h[p]<h[t]) t=p;
    if(p+1<=idx&&h[p+1]<h[t]) t=p+1;
    if(t!=u){
        h_swap(t,u);
        down(t);  //递归处理，直到不能下移
    }
}
 
void up(int u){
    int t=u>>1;
    if(t&&h[u]<h[t]){
        h_swap(t,u);
        up(t);  //递归处理，直到不能上移
    }
}
 
int main(){
    cin>>n;
    while(n--){
        string op;
        int k,x;
        cin>>op;
        if(op=="I"){
            cin>>x;
            idx++,m++;
            ph[m]=idx,hp[idx]=m;  //记录映射关系
            h[idx]=x;  //在末尾插入x
            up(idx);  //上移x
        }
        else if(op=="PM"){
            cout<<h[1]<<endl;
        }
        else if(op=="DM"){
            h_swap(1,idx);  //将最后插入的数覆盖h[1]
            idx--;
            down(1);  //将改变后的h[1]下移
        }
        else if(op=="D"){
            cin>>k;
            k=ph[k];  //找到第k个数对应的idx
            h_swap(k,idx);  //将最后插入的数覆盖h[k]
            idx--;
            down(k);  //将改变后的h[1]下移或上移动，down(k)和up(k)只会执行其一
            up(k);
        }
        else{
            cin>>k>>x;
            k=ph[k],h[k]=x;  //找到第k个数对应的idx，并将h[k]改变为x
            down(k);  //将改变后的h[k]下移或上移动，down(k)和up(k)只会执行其一
            up(k);
        }
    }
    return 0;
}

2.5 哈希表

概念

对于处理复杂大量的信息，我们将这些信息映射到一个容易操作的区间内，如将-1e9~1e9范围的数映射到0~1e5的范围内，以便于我们对这些数据进行插入，查询，删除等操作。

2.5.1 模拟散列表存储

操作思想(拉链法)

取质数N = 1e6+3作为映射的标准(一般来说，质数造成的冲突更小)
对于一组数据，将映射作为一维数组的下标来存储
如果对于两个不同的数据，他们的映射相同，则在该映射下新建一个结点来存储，解决冲突

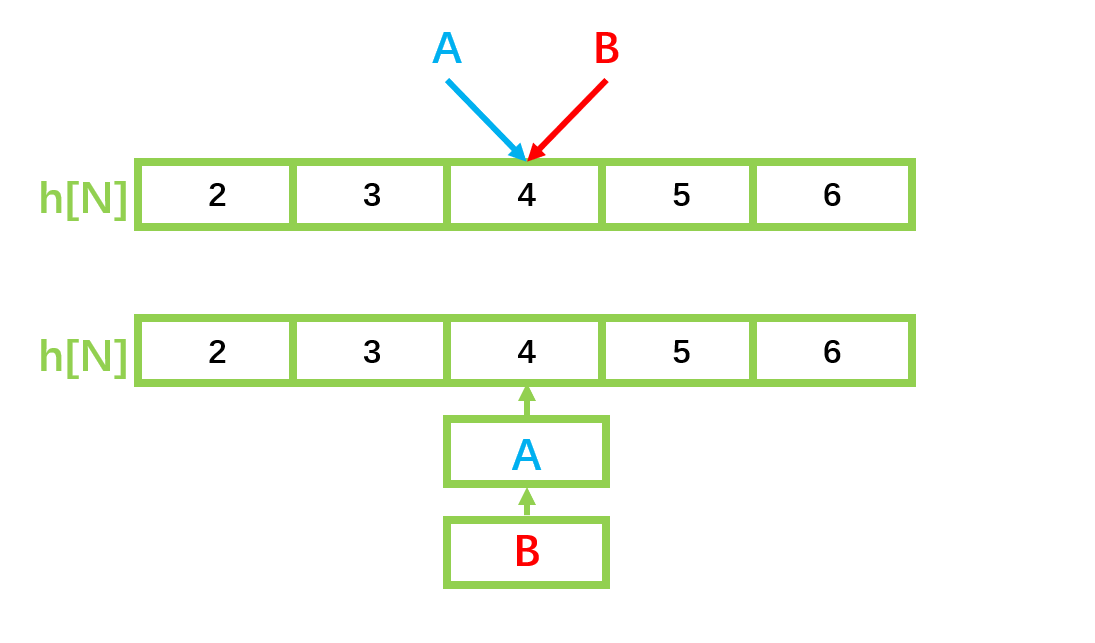
模板

 const int N=1e6+3;  //映射的标准
 
int h[N],e[N],ne[N];  //h[N]存储映射，初始化为-1 e[N]存储原值 ne[N]存储下一个结点的指针
 
int idx;  //充当指针作用
 
void init(){  //初始化操作
    for(int i=0;i<N;i++) h[i]=-1;
}
 
void insert(int x){  //插入操作
    int k=(x%N+N)%N;  //对N取模，保证结果为正整数
    e[idx]=x;
    ne[idx]=h[k];
    h[k]=idx++;
}
 
bool find(int x){  //查询操作
    int k=(x%N+N)%N;  //找到映射的下标
    for(int i=h[k];i!=-1;i=ne[i]){  //遍历映射，查询是否存在原值
        if(e[i]==x) return 1;
    }
    return 0;
}

例题 840. 模拟散列表

原题链接

描述

维护一个集合，支持如下几种操作：

I x，插入一个数 x；
Q x，询问数 x 是否在集合中出现过；

现在要进行 N 次操作，对于每个询问操作输出对应的结果。

输入格式
第一行包含整数 N，表示操作数量。

接下来 N 行，每行包含一个操作指令，操作指令为 I x，Q x 中的一种。

输出格式
对于每个询问指令 Q x，输出一个询问结果，如果 x 在集合中出现过，则输出 Yes，否则输出 No。

每个结果占一行。

数据范围
1≤N≤105
−109≤x≤109
输出样例：

 Yes
No

代码

 #include <bits/stdc++.h>
using namespace std;
 
const int N=1e6+3;
 
int h[N],e[N],ne[N];
 
int idx;
 
void insert(int x){
    int k=(x%N+N)%N;
    e[idx]=x;
    ne[idx]=h[k];
    h[k]=idx++;
}
 
bool find(int x){
    int k=(x%N+N)%N;
    for(int i=h[k];i!=-1;i=ne[i]){
        if(e[i]==x) return 1;
    }
    return 0;
}
 
int main(){
 
    for(int i=0;i<N;i++) h[i]=-1;
 
    int n;
    cin>>n;
    while(n--){
        char op[10];
        int x;
        scanf("%s %d",op,&x);
        if(*op=='I'){
            insert(x);
        }
        else{
            if(find(x)) puts("Yes");
            else puts("No");
        }
    }
    return 0;
}

2.5.2 字符串前缀哈希

操作思想

把字符串变成一个P进制数字，实现不同的字符串映射到不同的数字
对形如 X1 X2 X3⋯Xn−1 Xn 的字符串,采用字符的ASCII码乘上 P 的次方来计算哈希值
映射处理为该哈希值对Q进行取模:(X1 * P^n−1 + X2 * P^n−2+⋯+ Xn−1 * P^1 + Xn * P^0)%Q

注意点

任意字符不可以映射成0，否则会出现不同的字符串都映射成0的情况，比如A,AA,AAA皆为0
冲突问题：P = (131 或 13331) , Q = 2 ^ 64，一般情况下不产生冲突。
对于Q取模，我们用unsigned long long自然溢出来解决

模板

 typedef unsigned long long ULL;
 
const ULL N=1e6+3,P=131;
 
ULL h[N],p[N]; // h[k]存储字符串前k个字母的哈希值, p[k]存储 P^k mod 2^64
 
string s;  
cin>>s;  //读入字符串s
 
// 初始化前i个字符的哈希值
p[0]=1;
for(int i=1;i<=s.size();i++){
    h[i]=h[i-1]*P+s[i];  //前缀和求整个字符串的哈希值
    p[i]=p[i-1]*P;  //存储每一位的权值
}
 
// 计算子串str[l~r]的哈希值
ULL find(int l, int r){
    return h[r]-h[l-1]*p[r-l+1];  //将h[l-1]的高位与h[r]的最高位置的权值相对齐
}

例题 841. 字符串哈希

原题链接

描述

给定一个长度为 n 的字符串，再给定 m 个询问，每个询问包含四个整数 l1,r1,l2,r2，请你判断 [l1,r1] 和 [l2,r2] 这两个区间所包含的字符串子串是否完全相同。

字符串中只包含大小写英文字母和数字。

输入格式
第一行包含整数 n 和 m，表示字符串长度和询问次数。

第二行包含一个长度为 n 的字符串，字符串中只包含大小写英文字母和数字。

接下来 m 行，每行包含四个整数 l1,r1,l2,r2，表示一次询问所涉及的两个区间。

注意，字符串的位置从 1 开始编号。

输出格式
对于每个询问输出一个结果，如果两个字符串子串完全相同则输出 Yes，否则输出 No。

每个结果占一行。

数据范围
1≤n,m≤105

 8 3
aabbaabb
1 3 5 7
1 3 6 8
1 2 1 2

输出样例：

 Yes
No
Yes

代码

 #include <bits/stdc++.h>
using namespace std;
 
typedef unsigned long long ULL;
 
const int N=1e6+3,P=131;
 
ULL h[N],p[N];
 
ULL find(int l,int r){
    return h[r]-h[l-1]*p[r-l+1];
}
 
int main()
{ 
    int n,m;
    cin>>n>>m;
    string s;
    cin>>s;
 
    p[0]=1;
 
    for(int i=0;i<s.size();i++){
        p[i+1]=p[i]*P;
        h[i+1]=h[i]*P+s[i];
    }
 
    while(m--){
        int l1,l2,r1,r2;
        cin>>l1>>r1>>l2>>r2;
        if(find(l1,r1)==find(l2,r2)) cout<<"Yes"<<endl;
        else cout<<"No"<<endl;
    }
 
    return 0;
 
}

	10
	H 9
	I 1 1
	D 1
	D 0
	H 6
	I 3 6
	I 4 5
	I 4 5
	I 3 4
	D 6

STATISTICS

2.1 链表

2.1.1 单链表

2.1.2 双链表

2.2 栈

2.1.1 模拟栈

2.1.2 单调栈

2.3 队列

2.3.1 模拟队列

2.3.2 单调队列

2.4 堆

2.4.1 堆排序

2.4.2 可操作的堆

2.5 哈希表

2.5.1 模拟散列表存储

2.5.2 字符串前缀哈希

2.6 串（待补全）

2.6.1 KMP

2.6.2 Tire树

2.7 并查集（待补全）

发送评论编辑评论

2.1 链表

2.1.1 单链表

2.1.2 双链表

2.2 栈

2.1.1 模拟栈

2.1.2 单调栈

2.3 队列

2.3.1 模拟队列

2.3.2 单调队列

2.4 堆

2.4.1 堆排序

2.4.2 可操作的堆

2.5 哈希表

2.5.1 模拟散列表存储

2.5.2 字符串前缀哈希

2.6 串（待补全）

2.6.1 KMP

2.6.2 Tire树

2.7 并查集（待补全）

分享到微信

发送评论 编辑评论

推荐文章

发送评论编辑评论