本文最后更新于 1353 天前,其中的信息可能已经有所发展或是发生改变。
1102. 移动骑士
描述
给定一个 n∗n 的棋盘,以及一个开始位置和终点位置。
棋盘的横纵坐标范围都是 0∼n。
将一个国际象棋中的骑士放置在开始位置上,请问将它移动至终点位置至少需要走多少步。
一个骑士在棋盘上可行的移动方式如下图所示:
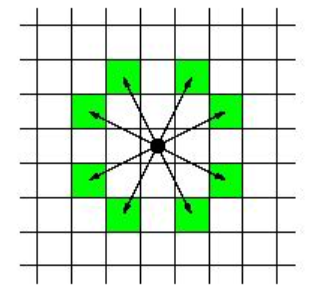
输入格式
第一行包含整数 T,表示共有 T 组测试数据。
每组测试数据第一行包含整数 n,表示棋盘大小。
第二行包含两个整数 x,y 用来表示骑士的开始位置坐标 (x,y)。
第三行包含两个整数 x,y 用来表示骑士的终点位置坐标 (x,y)。
输出格式
每组数据输出一个整数,表示骑士所需移动的最少步数,每个结果占一行。
数据范围
4≤n≤300,
0≤x,y≤n
输入样例:
3
8
0 0
7 0
100
0 0
30 50
10
1 1
1 1输出样例:
5
28
0分析
- 根据题意建立相关的偏移量数组
- 利用
BFS搜索遍历棋盘得到答案
#include <bits/stdc++.h>
using namespace std;
const int N=510;
bool vis[N][N];
int ans[N][N];
int dx[]={-1,-2,1,2,-2,-1,1,2},dy[]={-2,-1,-2,-1,1,2,2,1}; //建立偏移量数组
int t;
int n;
int s1,s2,e1,e2;
struct point{ //初始化point为struct类型
int x,y;
};
int bfs(){
queue<point> st; //初始化队列
st.push({s1,s2}); //将起始点信息入队
vis[s1][s2]=1; //标记该点已经走过
while(!st.empty()){
auto p=st.front();
st.pop();
for(int i=0;i<8;i++){
int l=p.x+dx[i],r=p.y+dy[i];
if(!vis[l][r]&&l>=0&&l<n&&r>=0&&r<n){ //判断是否满足搜索条件
ans[l][r]=ans[p.x][p.y]+1; //更新答案的距离
vis[l][r]=1; //标记该点为走过
if(l==e1&&r==e2) return ans[l][r]; //提前搜到该点直接返回答案
st.push({l,r}); //将该点入队
}
}
}
return ans[e1][e2];
}
int main(){
cin>>t;
while(t--){
//多实例,将其清空初始化
memset(vis,0,sizeof vis);
memset(ans,0,sizeof ans);
cin>>n;
cin>>s1>>s2;
cin>>e1>>e2;
cout<<bfs()<<endl;
}
}